相机标定对于联系相机测量和真实三维世界测量也很重要。它的重要性在于场景不仅仅是三维的，也是物理单位度量的空间。因此，确定相机的自然单位(像素)与物理单位(如mm)的关系是三维场景重构的重要部分。相机标定的过程既给出相机的几何模型又给出透镜的畸变模型，这两个模型定义了相机的内参。

单应性变换(homography transform)：它是一种能反应相机基本行为、各种失真和矫正特性的数学工具。

所述知识是为了建立足够的理论以便让读者可以真正理解cv::calibrateCamera()，并知道其内涵。

1、相机模型

   

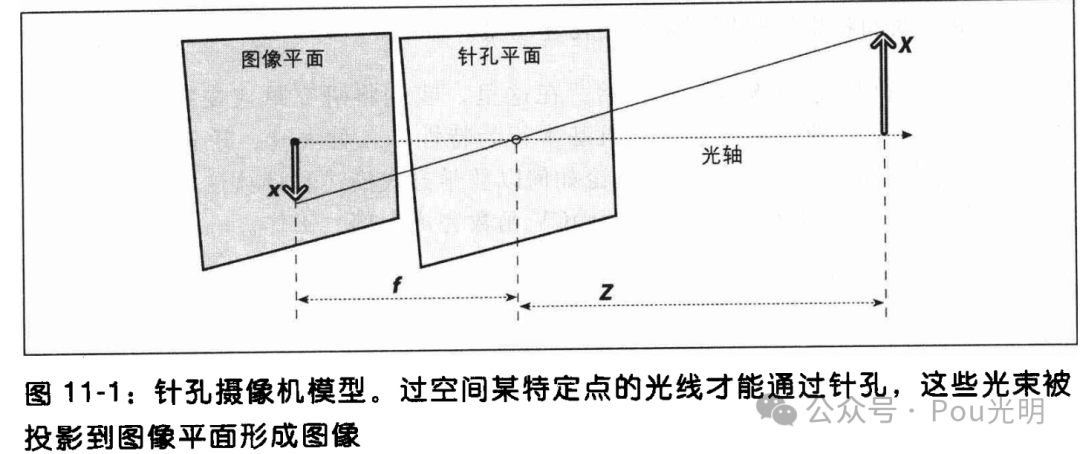
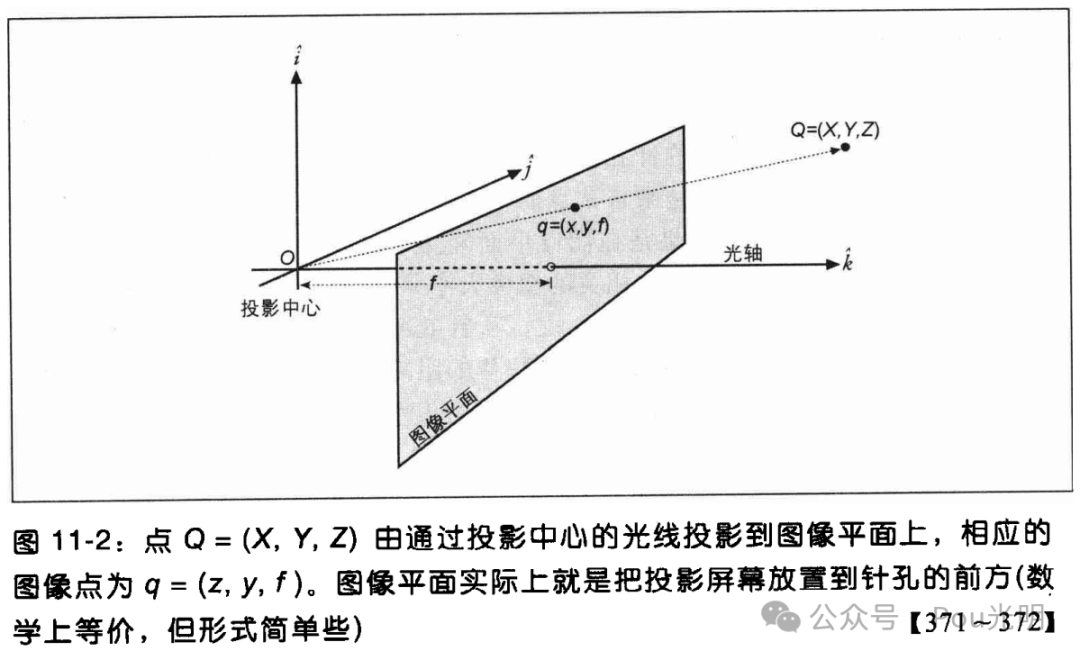
重新把针孔相机模型整理为另一种等价形式，使其数学形式更简单一些。如图，交换针孔和图像平面，主要差别是现在物体出现在等式右边。针孔中的点被理解为投影中心。这样，每一条光线，从远处物体的某个点出发，到达投影平面的中心。光轴与图像平面的交点被称为主点。在这个与旧的投影平面等价的新前端图像平面上，远处物体的图像与图11-1中的图像大小完全一致。光束与图像平面的相交生成图像，而平面到投影中心的距离是f。这样形成更容易理解的三角形相似关系 x/f=X/Z.负号被去掉了。因为目标图像不再是倒立的。

你也许认为主点即等于成像仪的中心，但这意味着某些人拿着镊子和胶水要把摄像机里面的成像仪以微米级别的精度安装。实际上，芯片的中心通常不在光轴上。因此，引入Cx和Cy对可能得偏移(对光轴而言)进行建模。则：    

2、基本投影几何

将坐标(X，Y，Z)的物理点Q映射到投影平面上坐标为(x,y)的点的过程叫投影变换。采用这种变换，可以方便地使用我们所熟知的齐次变换。齐次坐标把维数为n投影空间上的点用(n+1)维向量表示，其额外限制是任何两点的交比不变。这样允许我们将定义摄像机的参数(fx，fy，cx，cy)重新排列为一个3×3矩阵，该矩阵称为相机的内参矩阵。

Opencv中，相机的内参矩阵(opencv求解相机内参矩阵使用的方法源自Heikkila和Silven).    

讨论齐次坐标时，opencv库中有一个函数cvConvertPointHomogenious()，使用该函数可以很方便地对齐次坐标进行转换。

   

欢迎关注：