国考省考行测:图形推理,数量规律
2022找工作是学历、能力和运气的超强结合体!
公务员特招重点就是专业技能,附带行测和申论,而常规国考省考最重要的还是申论和行测,所以大家认真准备吧,我讲一起屡屡申论和行测的重要知识点
遇到寒冬,大厂不招人,可能很多算法学生都得去找开发,测开
测开的话,你就得学数据库,sql,oracle,尤其sql要学,当然,像很多金融企业、安全机构啥的,他们必须要用oracle数据库
这oracle比sql安全,强大多了,所以你需要学习,最重要的,你要是考网络警察公务员,这玩意你不会就别去报名了,耽误时间!
除了技术,申论和行测也得好好准备
文章目录
- 国考省考行测:图形推理,数量规律
- @[TOC](文章目录)
- 行测:国考省考行测:图形推理,数量规律
- 线的数量
- 常规考察
- 直线数,曲线数,曲直线数
- 细化考察
- 平行线的对数
- 平行线的条数,横线,数线
- 内部外部线的数量
- 线段个数
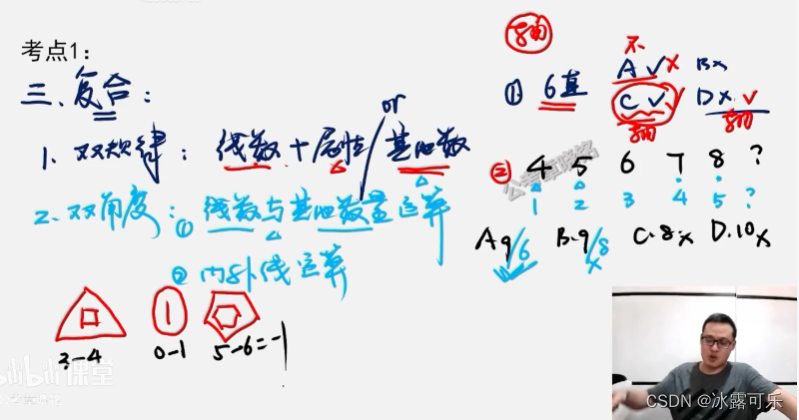
- 复合考察
- 双规律:线+属性规律,其他规律
- 双角度:线数量+其他数运算
- 特殊的线数量:笔画数
- 标志图,日,T,X
- 笔画个数的判断方法
- 面 的数量——常考
- 常规考察:面的总数量
- 细化考察
- 相同面的对数,个数
- 直面,曲面构成的数量
- 内部,或外部的面
- 三角形特殊,都有三角形,可能只需要数三角形的数量
- 图形只有三角形和四边形2种,总面数没规律,两者之间的运算
- 复合考察
- 双规律:面数+属性+数量
- 双角度复合
- 交点的数量
- 常规考察:交点的总数量
- 细化
- 复合考察
- 爽规律:交点数+属性
- 双角度
- 元素的数量
- 常规:元素的总个数或种类数
- 细化考察
- 复合考察少
- 角的数量
- 常规:角的总数
- 角的细化:
- 复合考察:
- 立体图的规律
- 视图:看:
- 三视图
- 截面图
- 正方体截面
- 圆柱体的截面图
- 圆锥切
- 立体拼合图
文章目录
- 国考省考行测:图形推理,数量规律
- @[TOC](文章目录)
- 行测:国考省考行测:图形推理,数量规律
- 线的数量
- 常规考察
- 直线数,曲线数,曲直线数
- 细化考察
- 平行线的对数
- 平行线的条数,横线,数线
- 内部外部线的数量
- 线段个数
- 复合考察
- 双规律:线+属性规律,其他规律
- 双角度:线数量+其他数运算
- 特殊的线数量:笔画数
- 标志图,日,T,X
- 笔画个数的判断方法
- 面 的数量——常考
- 常规考察:面的总数量
- 细化考察
- 相同面的对数,个数
- 直面,曲面构成的数量
- 内部,或外部的面
- 三角形特殊,都有三角形,可能只需要数三角形的数量
- 图形只有三角形和四边形2种,总面数没规律,两者之间的运算
- 复合考察
- 双规律:面数+属性+数量
- 双角度复合
- 交点的数量
- 常规考察:交点的总数量
- 细化
- 复合考察
- 爽规律:交点数+属性
- 双角度
- 元素的数量
- 常规:元素的总个数或种类数
- 细化考察
- 复合考察少
- 角的数量
- 常规:角的总数
- 角的细化:
- 复合考察:
- 立体图的规律
- 视图:看:
- 三视图
- 截面图
- 正方体截面
- 圆柱体的截面图
- 圆锥切
- 立体拼合图
行测:国考省考行测:图形推理,数量规律
难度高,次于属性
图形组成凌乱,在属性规律走不通,答案不唯一,就要考虑数量规律了
先把图变成数字
再借助数字看规律
线,面,交点,角,元素,变完数字
数字等差,常数数列
地推数列
周期数列

其他考法难
奇偶数列
gg
2的倍数
3的倍数
乱序少数

对称数列

平方运算

拉
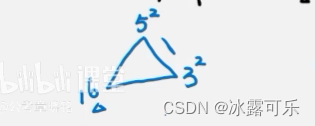
图形推理考这种,恶心人
还不如直接数字呢
元素换算

1–4为主
线的数量
常规考察
直线数,曲线数,曲直线数
线看属性,再考虑数量哈

作差,作和
乘除
骚啊
被2整除,骚啊
细化考察
平行线的对数

平行线的条数,横线,数线
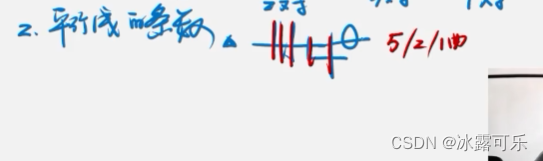
考的少了
内部外部线的数量

线段个数

几段数量
三角形个数

复合考察
双规律:线+属性规律,其他规律
联合交点数量啥的,拉胯
考的多
国考难
双角度:线数量+其他数运算
内外线运算
特殊的线数量:笔画数
隐含的经常考一笔画
标志图,日,T,X
圆套
三角形
切
五角星
多头线
+
分离的图

笔画个数的判断方法
【1】独立的完整图,笔画数是=奇数点数的点/2
发出奇数条线数量的点
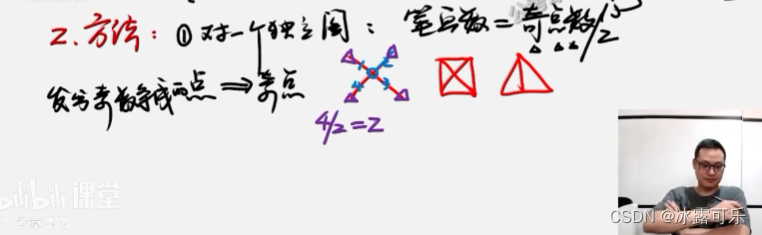
断点,发出了条数量
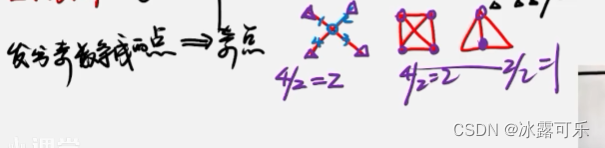
奇点一定是0或2的倍数
——
2个奇点
一笔画,奇点数是0/2
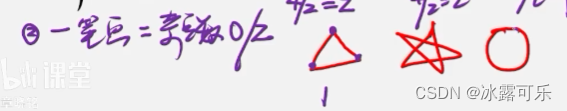
0奇点

分离的图,各自数,再算奇点

汉字的话,单数数哦
不是看奇点哈


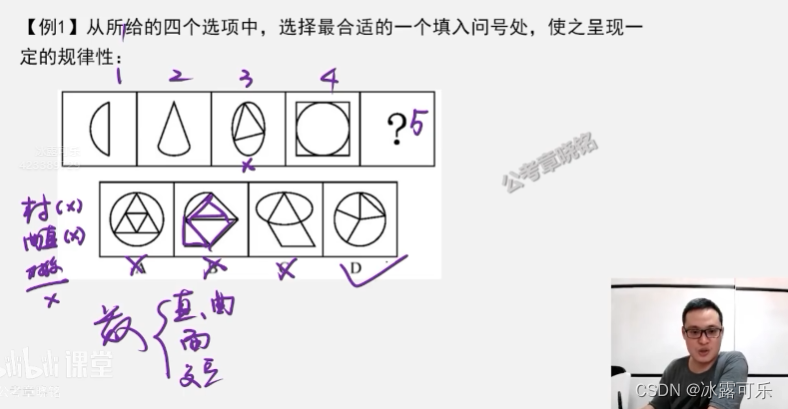
曲线都是1条
直线递增数量
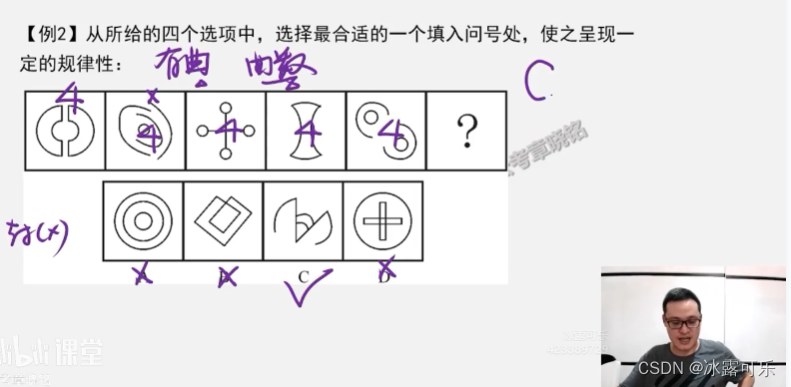
曲线数量
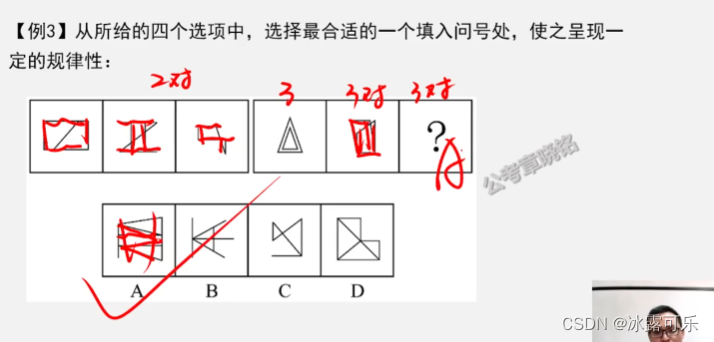
平行线对shu
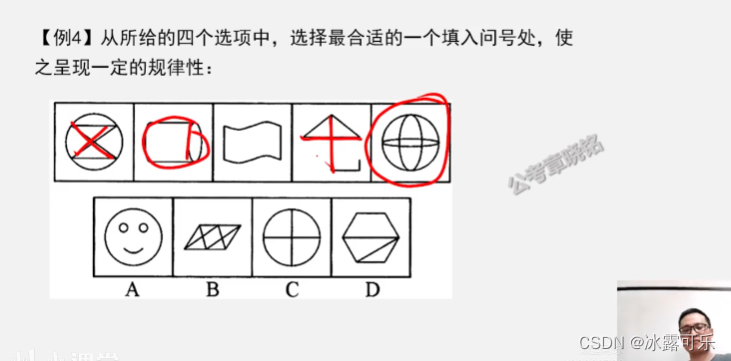
笔画
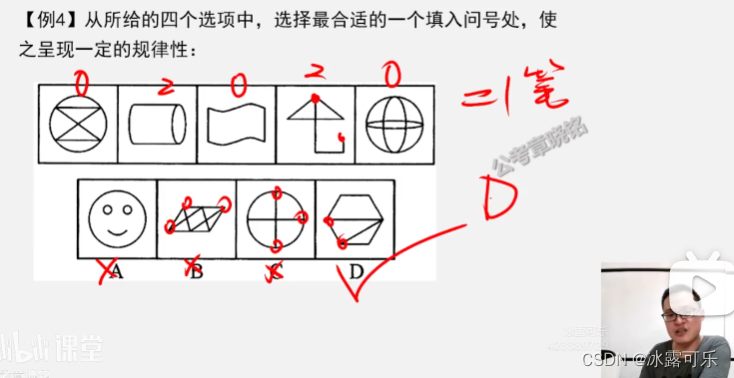
奇点02才是一笔画
否则gg
三角套
笔画可能
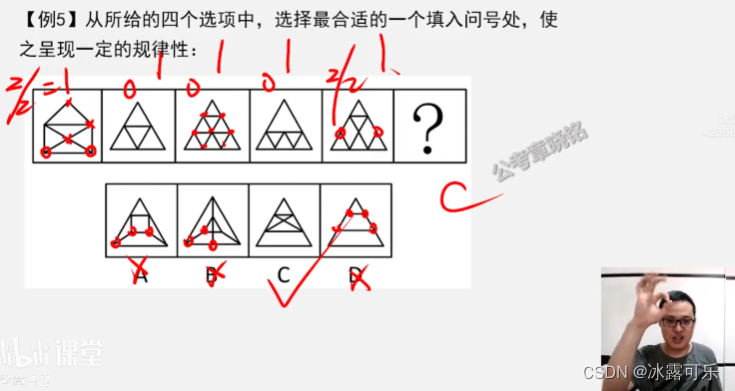
一笔画
骚啊
未必能想到
最难的
骚狗
骚
面 的数量——常考
常规考察:面的总数量
图形乱,封闭的空白区域很明显,想到面的特征
A
B
面好说
多少个面好数
空白的最小单元

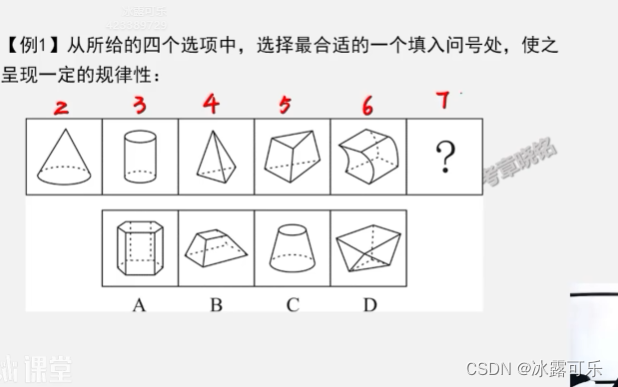
7面就行
细化考察
相同面的对数,个数

一对,相同的面
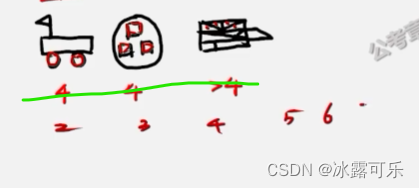
相同面的个数递增
直面,曲面构成的数量
内部,或外部的面

三角形特殊,都有三角形,可能只需要数三角形的数量
比如,把三角形数到最小

可能是4个哦
有2个大的三角形

高难度了

还有一种
图形只有三角形和四边形2种,总面数没规律,两者之间的运算
加减乘除
作差是常数
复合考察
双规律:面数+属性+数量
面+最大面/小面的特征
最大面是否有特点【难哦】

属性:对称性
曲直性
形状
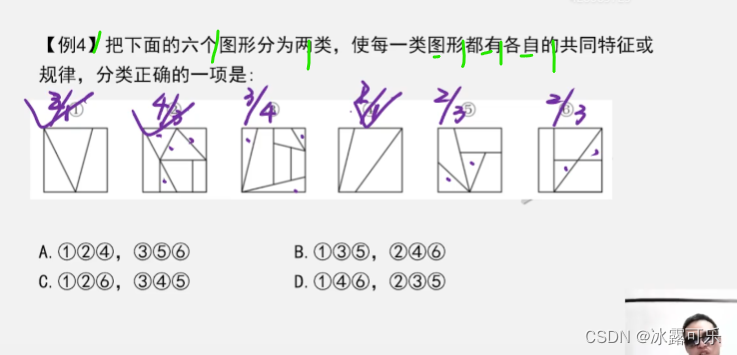
三角形很特殊
每个图中最大,最小就是三角形
面积站多少比例
双角度复合
面数+其他数的运算
最爱靠的是线数,直线,曲线
外边框的数量-面数

北京,上海,江苏爱考
直线最多
面数+笔画
笔画需要隐含找
奇点数/2就是笔画数

面数+对称轴数
面与对称轴之间的差

难度高,gg
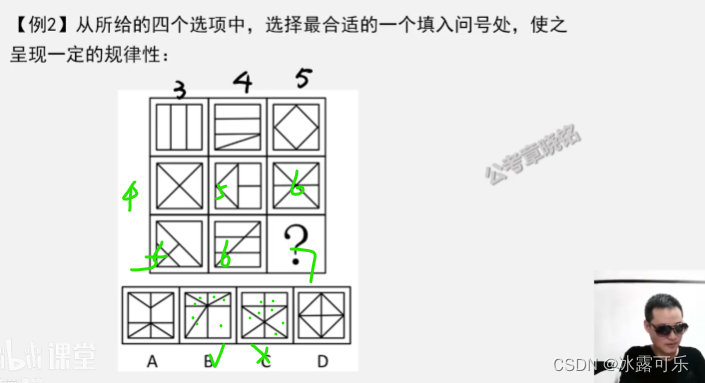

相同面
交点的数量
常规考察:交点的总数量

细化
直曲交点
切点
内部外框处交点

复合考察
爽规律:交点数+属性
交点数+其他角度,线,面
双角度
交点+其他数的运算
角,对称轴

对称轴难搞
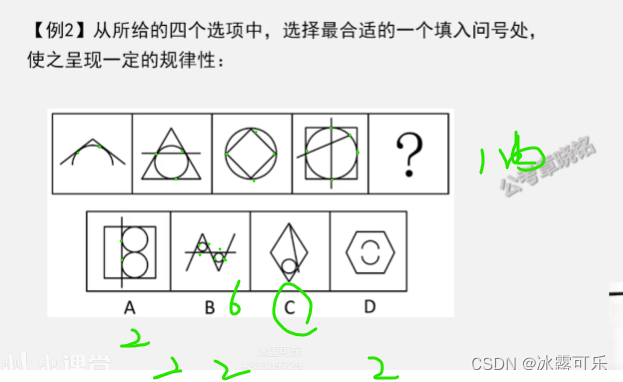
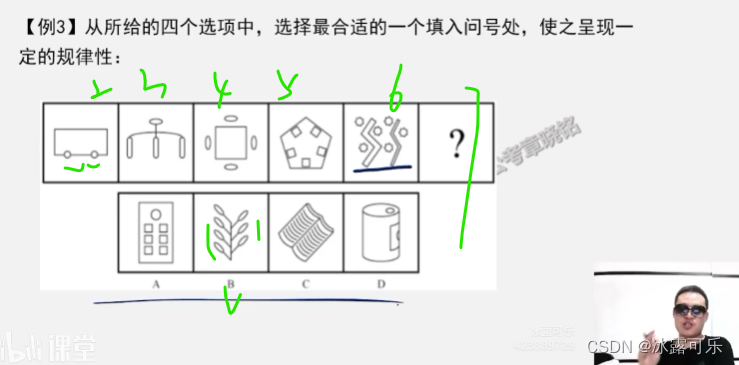
只有一条曲线
曲直交点数量递增
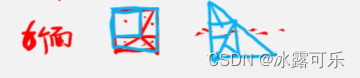
B
C是一条曲线
B最好
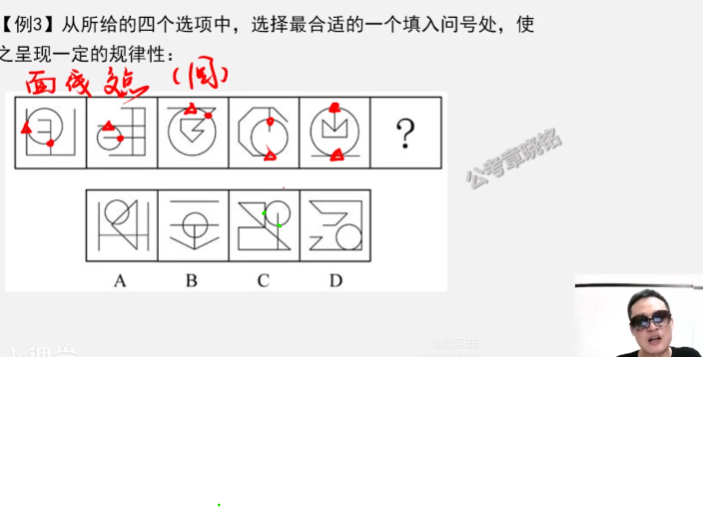
一个切点,一个交点


正方形发出点数
元素的数量
不必考,但是规律明显
常规:元素的总个数或种类数
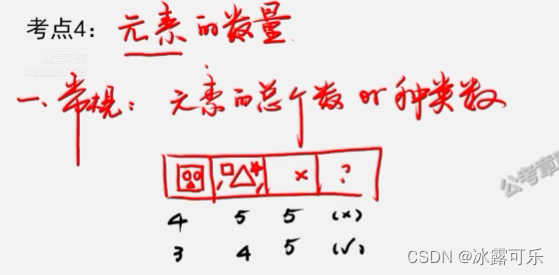
种类,同一样就是一种
图形,分散诸多小元素,可以典型考元素的种类或者个数
图形的组成部分数量也行
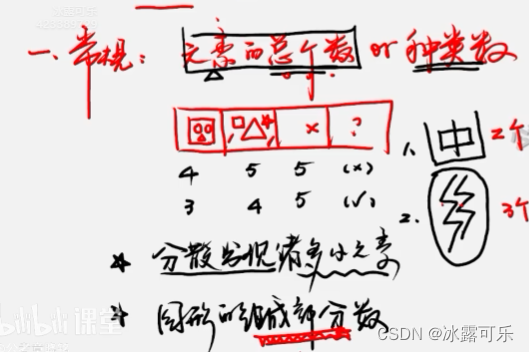
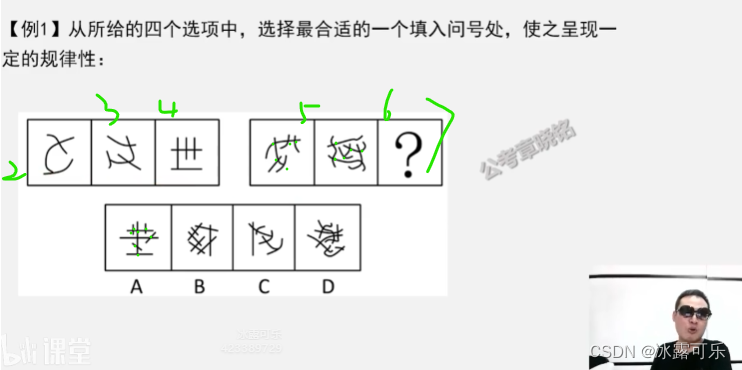
汉字可能考组成部分

细化考察
相同的元素
总个数,种类无规律
则可以数特定的一个共有元素
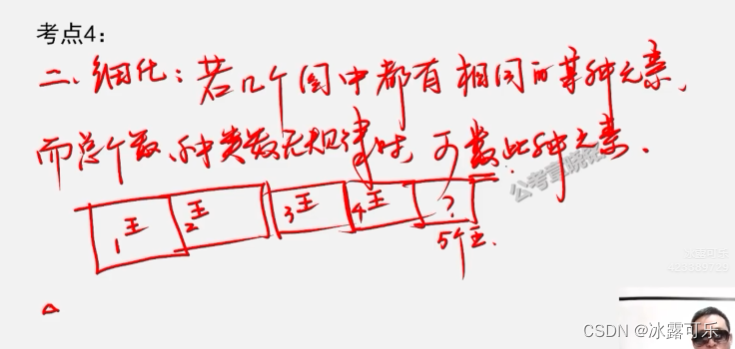
常考
复合考察少
爽规律复合
很难考角度
元素个数+属性
元素部分数+静态位置
点相连,而不是线相连
分散开
连接2个黑球
3个黑求链接

1-9缺啥补啥
15
横看,竖看都是求和为15
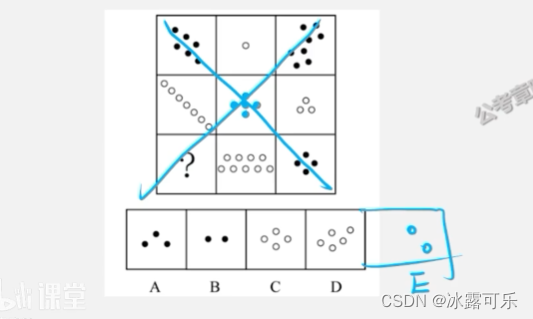
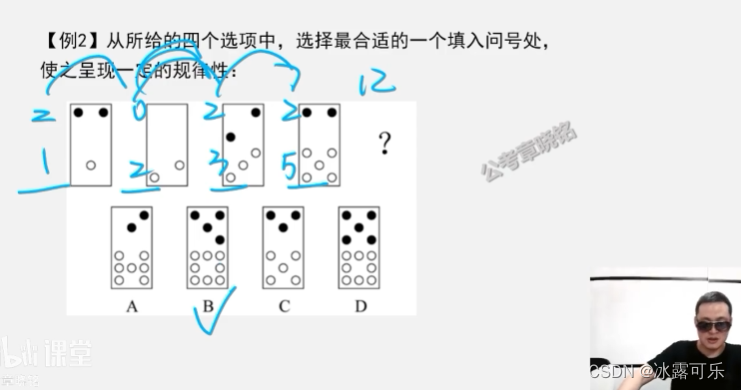
求和1+2=3
……
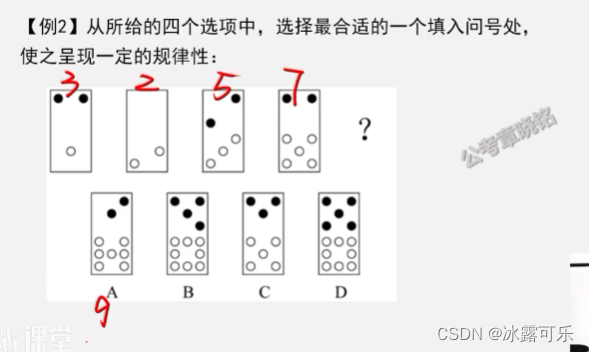
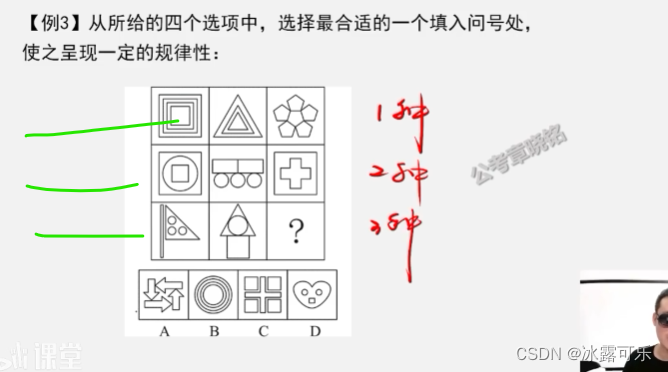
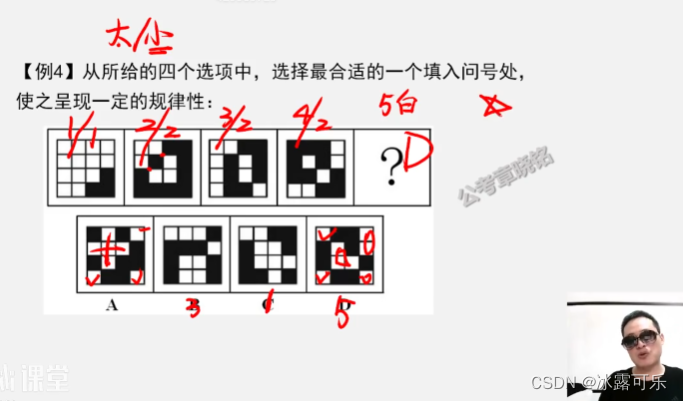
白色数量递增
区域
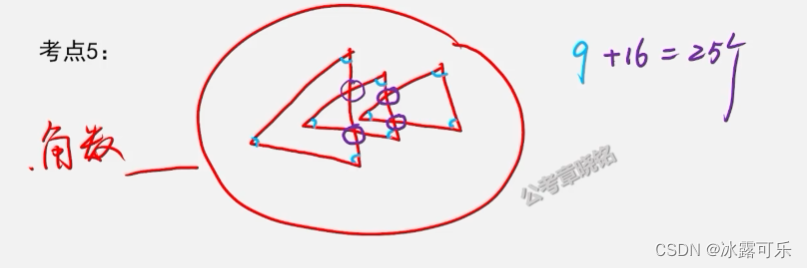
角的数量
常规:角的总数
方法:
45°
1个角
90°
1个角
三角形,可能多
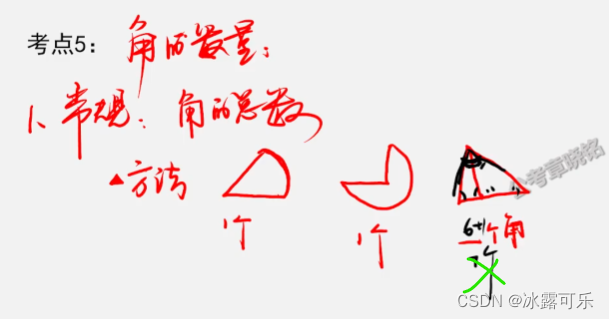
角是不能重复用
不是三角
懂?
角就是角
2个直线最小的角
中间且没有线,度数小于180
180直线不算角
懂吧?
角
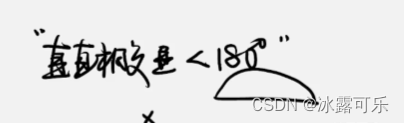
锯齿图
很特殊
心电图
角的细化:
直直角数90
锐角钝角
内部角,外部角
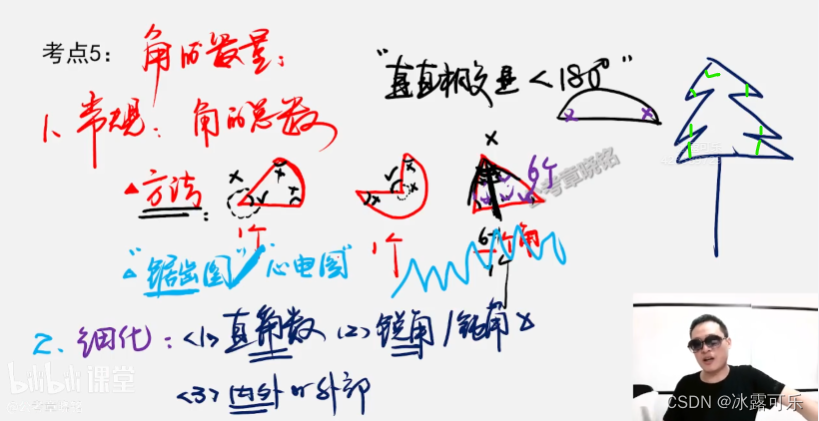
内部的角

有锯齿状,一定数角

看到直角,数直角
复合考察:
爽规律
角数+其他数
双角度:角数其他数运算

立体图的规律
位置,正四面体,六面体,已经讲过了
现在将其他的
题目直接告诉你立体图,具体图形具体分析
截面图,视图,立体拼合图
视图:看:
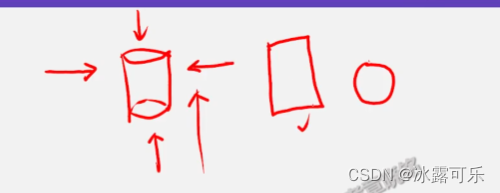
左右,前后,上下看
同心圆是圆锥
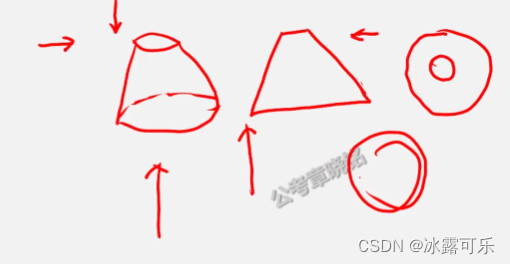
平面图,
方向性,很多东西看不到
阻挡看不到,
相交线不被阻挡,看得到
平滑过渡的相切线,看不到
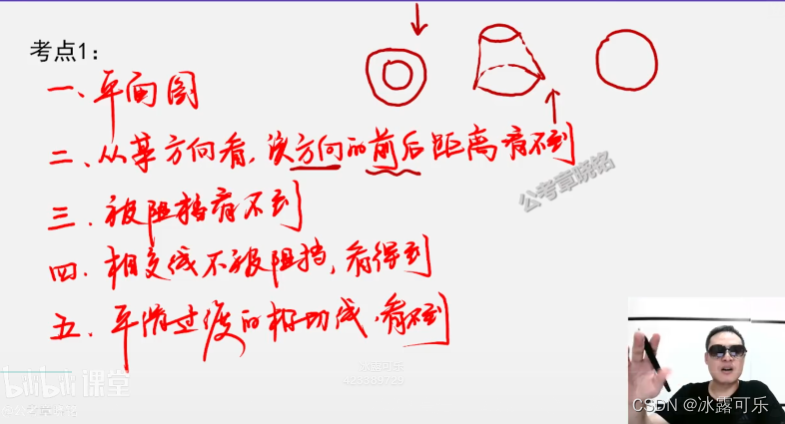


俯视图,有交面则有线条
平滑的就没有
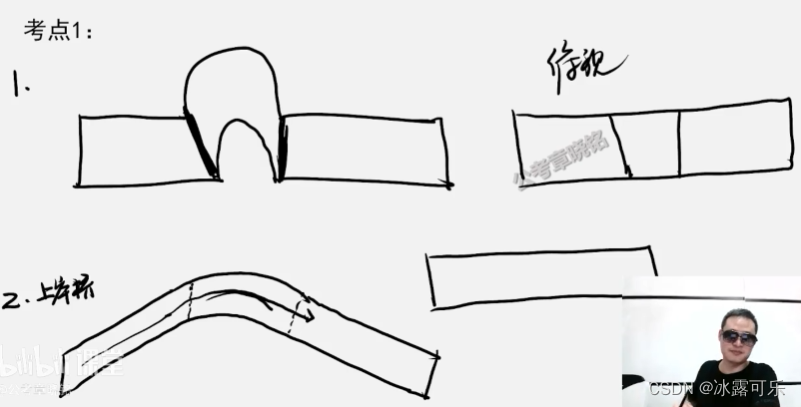
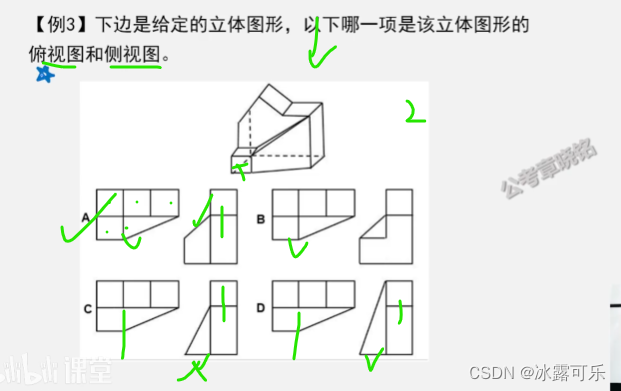
三视图
主视图正视图
侧视图,左视图,右视图
俯视图
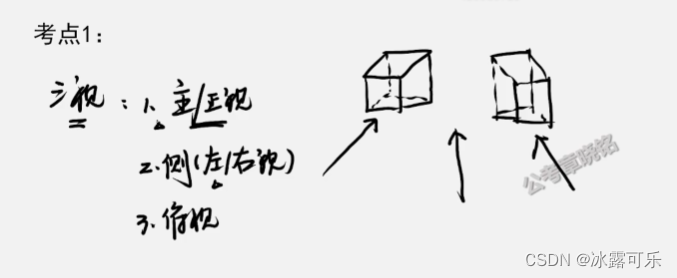
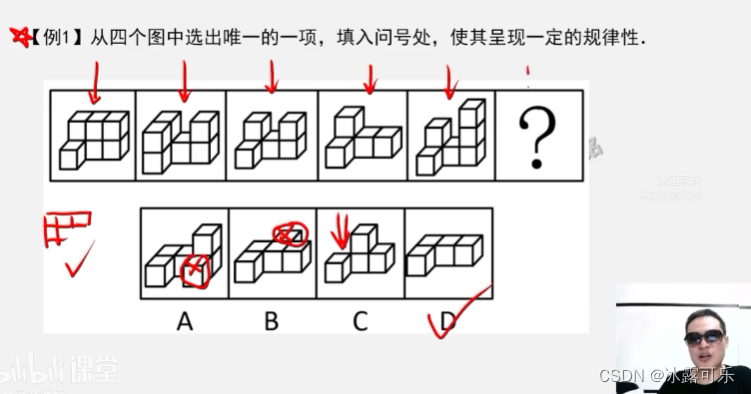
考视图的角度,骚啊
多个方块放一起可能就要考这个
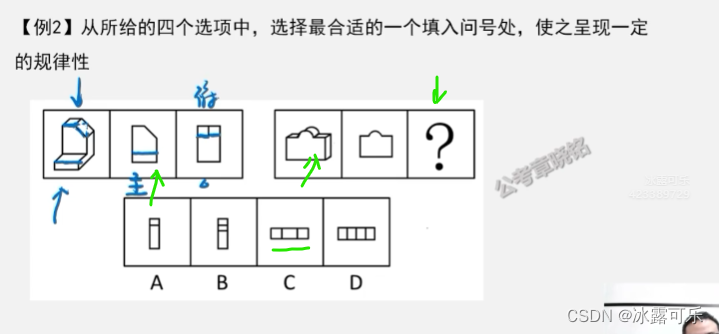
截面图
难度高一些
创新考法骚
一刀切一个立体,切出来之后长啥样
不可拐弯
一个平面最多截出1条线
曲面就不确定了
刀的切法有几种,水平,竖直,倾斜

图的构成可能是组合体,可能是镂空的体
很骚,中间有一个洞——白色标注
黑色实心,白的空心

不能封口
常规立体入手,做为入手
正方体截面
能截除3–6边型
斜着下刀
锐角,不会是直角,钝角
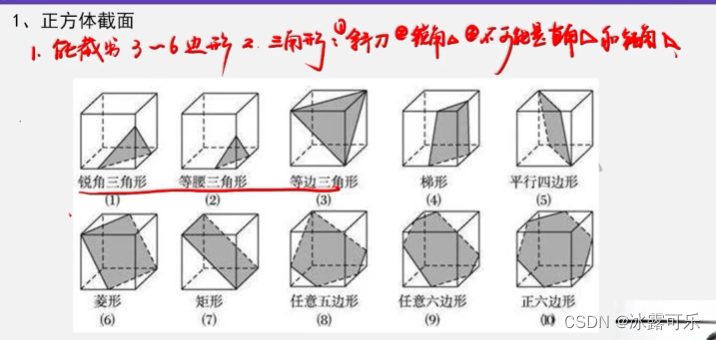
四边形:
刀不重要
重要的是四边形,不能截图出直角梯形。
普通梯形可以
五边形
不能正五边形,普通五边形
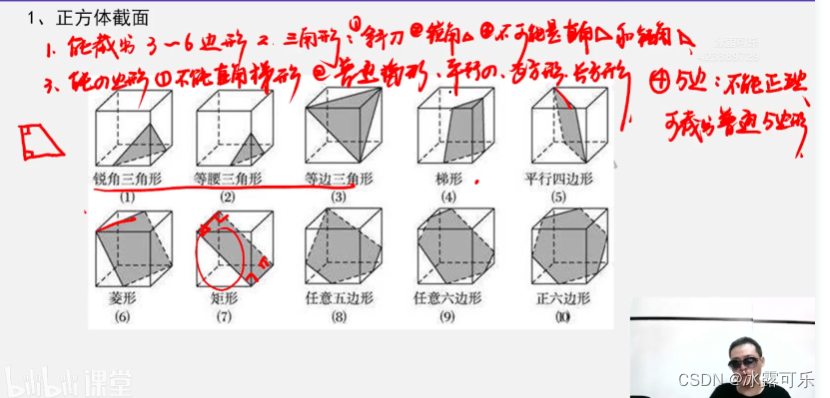
正六边形可以
圆柱体的截面图
横着
竖着
斜着
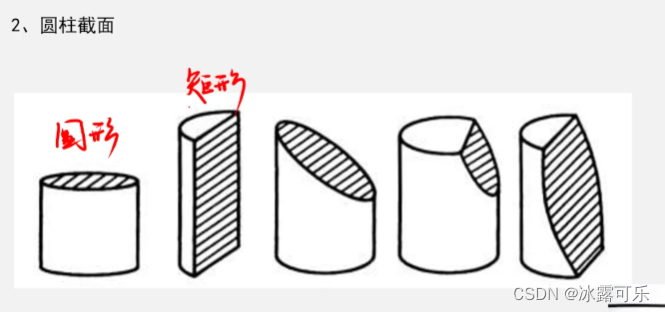
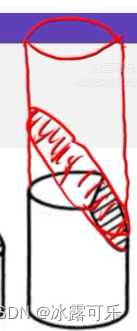
部分椭圆

竖着就是圆柱
圆锥切
圆
椭圆:对称
抛物线
双曲线
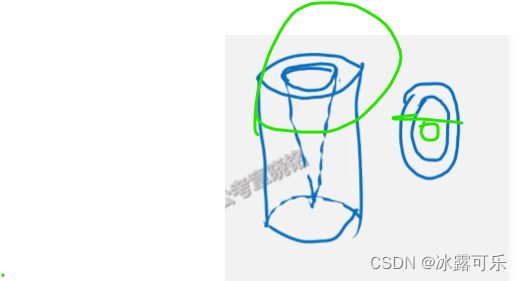
不能切同心圆
三角形
圆台

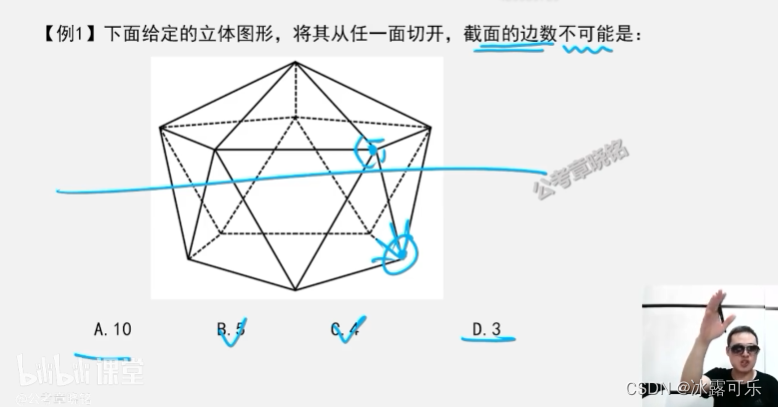
公共边多少就能切出来
3不行
最少得五个公共边
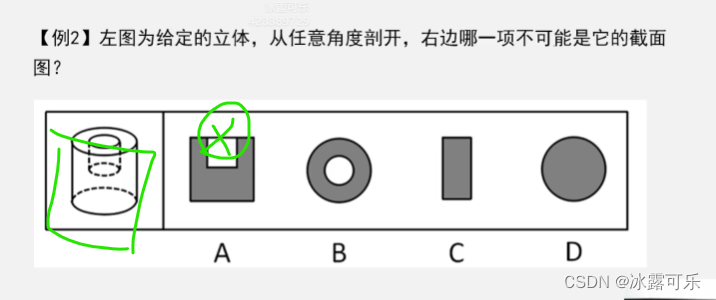
中间不能封口