题目

给定两个整数数组 preorder 和 inorder ，其中 preorder 是二叉树的先序遍历， inorder 是同一棵树的中序遍历，请构造二叉树并返回其根节点。

示例1

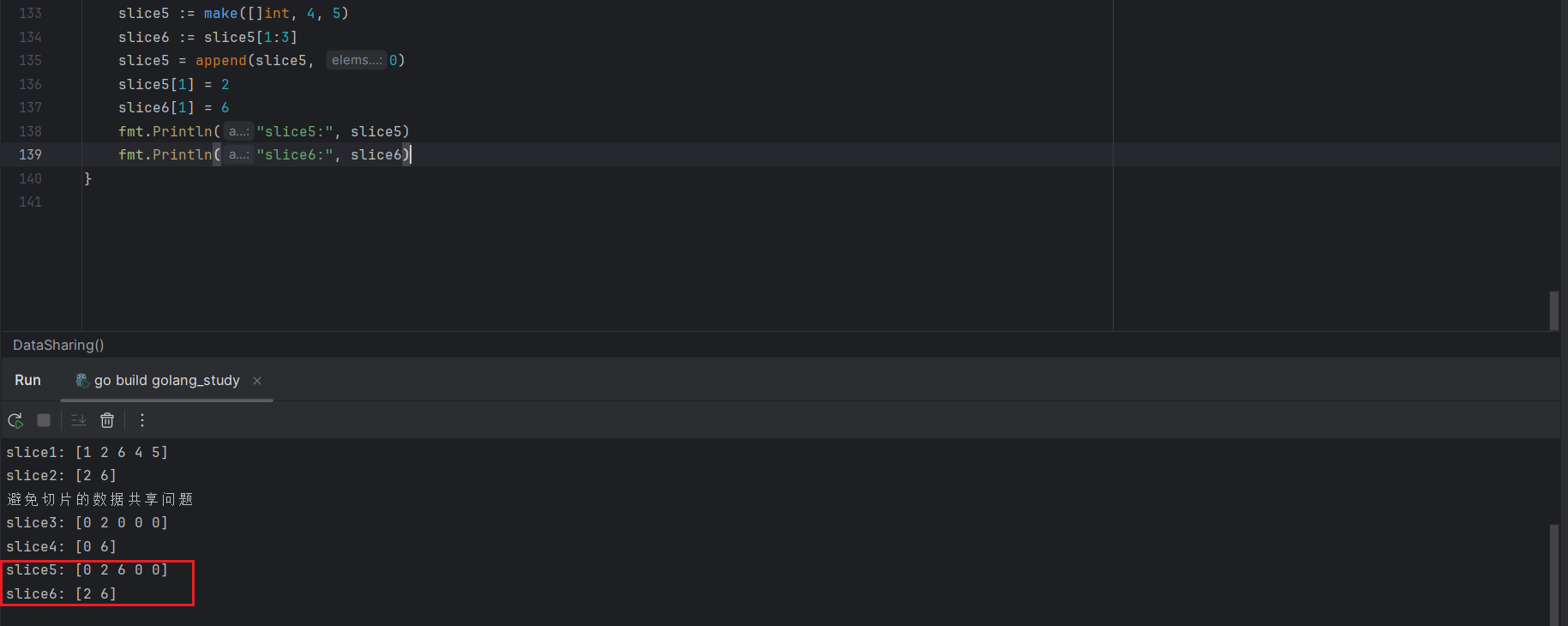
输入: preorder = [3,9,20,15,7], inorder = [9,3,15,20,7]
输出: [3,9,20,null,null,15,7]

示例2

输入: preorder = [-1], inorder = [-1]
输出: [-1]

• 1 <= preorder.length <= 3000
• inorder.length == preorder.length
• -3000 <= preorder[i], inorder[i] <= 3000
• preorder 和 inorder 均无重复元素
• inorder 均出现在 preorder
• preorder 保证为二叉树的前序遍历序列
• inorder 保证为二叉树的中序遍历序列

分析

二叉树前序数组的第一个元素一定是根节点，因为前序遍历的顺序是先遍历根节点在遍历左右子树。
而中序遍历是根节点的左子树都遍历完了才遍历根节点，所以在中序数组中，根节点前面的元素是他的左子树节点，后面的元素是他右子树的节点。
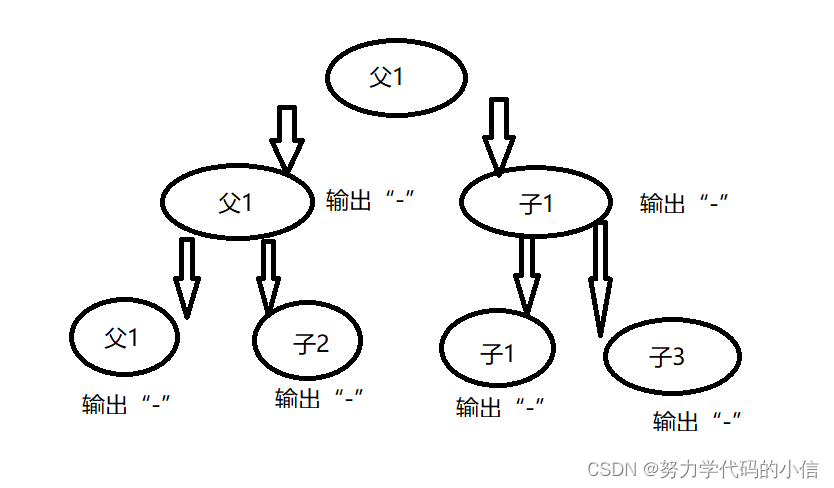
根据这个特性我们可以把中序数组和前序数组划分两部分，然后每部分继续按照上面的方法划分，直到只有一个节点，不能划分为止。比如示例 1 的数组划分如下图所示。

划分的时候我们没必要把数组进行截取，只需要使用几个变量分别记录下前序和中序数组的区间范围即可。因为我们是根据前序数组中的元素在中序数组中的位置来划分中序数组的，所以这里只需要记录中序数组的范围，前序数组只需要记录起始位置即可。

代码

public TreeNode buildTree(int[] preorder, int[] inorder) {
    // 为了方便后续进行查找，先把中序数组的所有值存储到map中
    Map<Integer, Integer> map = new HashMap<>();
    int length = inorder.length;
    for (int i = 0; i < length; i++)
        map.put(inorder[i], i);
    return build(preorder, map, 0, 0, length - 1);
}

private TreeNode build(int[] preorder, Map<Integer, Integer> map,
                       int preStart, int inStart, int inEnd) {
    if (inStart > inEnd) return null;// 表示数组被访问完了。
    // 使用前序数组的第一个元素创建根节点
    TreeNode root = new TreeNode(preorder[preStart]);
    // 查找根节点在中序数组中位置
    int index = map.get(root.val);
    int leftCount = index - inStart;// 左子树的所有节点个数
    // 前序数组区间划分：
    // [preStart, preStart]根节点
    // [preStart + 1, preStart + leftCount]左子树
    // [preStart + leftCount + 1, ……]右子树
    // 中序数组区间划分：
    // [inStart, index - 1]左子树
    // [index, index]根节点
    // [index + 1, inEnd]右子树
    root.left = build(preorder, map, preStart + 1, inStart, index - 1);
    root.right = build(preorder, map, preStart + leftCount + 1, index + 1, inEnd);
    return root;
}