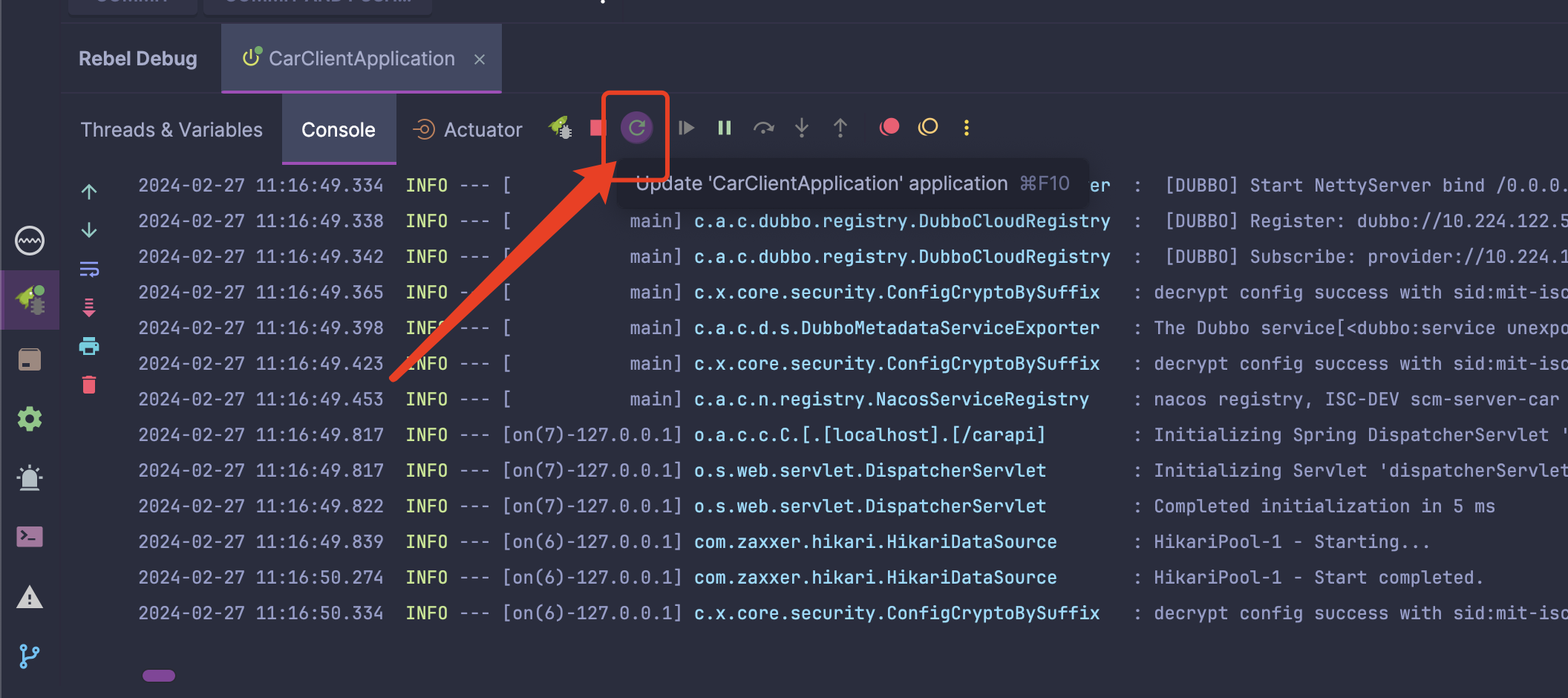
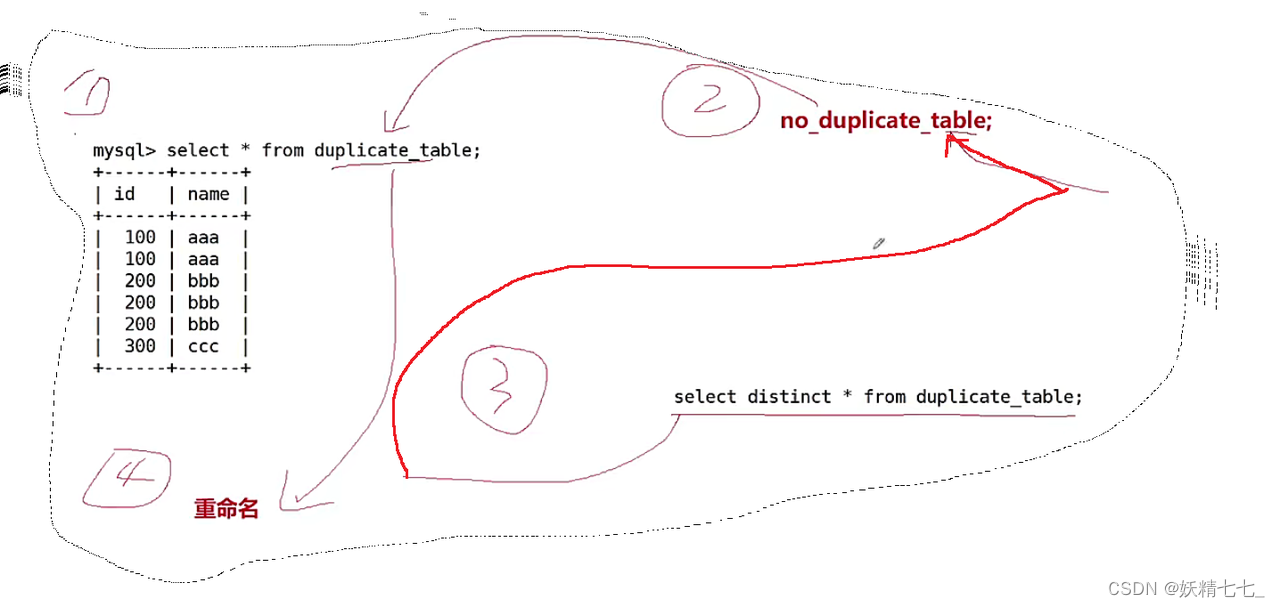
一.题目描述

二.输入描述

 

三.输出描述

 

 四.问题分析

几个两两互质的数，最大公约数是1，最小公倍数是他们的乘积。

两个互质的数a和b最小不能表示的数就是（a-1）（b-1）-1，即，两个互质的数a，b可以表示（a-1）（b-1）之后的所有数字。

此定理用于确定数字的上界。（100-1）*（99-1）-110000

如果两个数不互质，则只要不是这两个数最大公约数的倍数都凑不出来。

//包子凑数
#include <iostream>
#include <algorithm>

using namespace std;

const int MAX=1e5;//数字上限
bool d[MAX]={0};//表示是否能够凑出包子数为i的情况
int baozi[110],ans=0;

int gcd(int a,int b){
    if(a<b)
        swap(a,b);
    while(b){
        int x=a%b;
        a=b;
        b=x;
    }
    return a;
}

int main(int argc, const char * argv[]) {
    ios::sync_with_stdio(0);cin.tie(0);cout.tie(0);
    int n,g=0;
    cin>>n;
    for(int i=1;i<=n;i++){
        cin>>baozi[i];
        if(i==1)
            g=baozi[i];
        else
            g=gcd(g,baozi[i]);
    }
    if(g!=1){
        cout<<"INF"<<'\n';
    }
    else{
        d[0]=1;
        for(int i=1;i<=n;i++){
            for(int j=baozi[i];j<=MAX;j++){
                d[j]=d[j]|d[j-baozi[i]];
            }
        }
        for(int i=1;i<=MAX;i++){
            if(d[i]==0)
                ans++;
        }
    }
    cout<<ans;
    return 0;
}