https://link.springer.com/article/10.1007/s42452-019-0989-z
描述了构建零知识区间证明(ZKRP)的不同策略,例如2001年Boudot提出的方案;2008年Camenisch等人提出的方案;以及2017年提出的Bulletproofs。
Introduction
总结并比较了保护链上私人信息的两类方式,引出主旨ZKRP:
- 可信执行环境(TEE),如英特尔SGX技术。核心思想是,任何私人数据在区块链上必须以加密形式出现。只有底层加密密钥的所有者才能解密它。对这些信息的验证必须在TEE系统中进行,其中可以嵌入加密密钥。因此,私人数据只有在解密后才可见,这发生在受控环境内。但易受分支预测和侧信道攻击的影响。
- 零知识证明(ZKP),进一步ZKRP证明一个秘密整数属于某个区间。
ZKRP的用例
ZKRP的应用案例:
- ZKRP可以用来证明某人超过18岁,
- 了解你的客户(KYC)
- 抵押风险评估。
- 评级和投资评级。与使用ZKRP k +1次的直接解决方案相比,可能存在更有效的构造。
- 电子投票
- 安全电子拍卖(如:获胜者支付第二高的出价、采购)
在DLT和区块链的具体场景中重要的应用:
- Confidential Transactions (CT),利用Pedersen承诺隐藏交易金额。用ZKRP验证交易金额的正确性
- Provisions是一种协议,它允许比特币交易所证明自己是有偿付能力的,通过显示每个账户都有正余额,并且还显示交易所的资金数量大于或等于系统中所有个人账户余额的总和。
ZKP
定义:非交互式零知识(Non-Interactive Zero Knowledge, NIZK)证明方案由算法Setup、Prove和Verify定义:
- p a r a m s = S e t u p ( λ ) params = Setup(\lambda) params=Setup(λ)
- p r o o f = P r o v e ( x , w ) proof =Prove(x,w) proof=Prove(x,w)
- b = V e r i f y ( p r o o f ) b=Verify(proof) b=Verify(proof)
Fiat–Shamir 启发式:将 interactive ZKP转换成NIZK。
缺点是,它使密码系统在随机oracle模型(ROM)下是安全的。
零知识证明方案具有以下性质:
- Completeness:给定一个满足实例 x x x的见证 w w w,得到 V e r i f y ( P r o v e ( x , w ) ) = 1 Verify(Prove(x, w)) = 1 Verify(Prove(x,w))=1。
- Soundness:如果见证 w w w不满足 x x x,则概率 P r o b [ V e r i f y ( P r o v e ( x , w ) ) = 1 ] Prob[Verify(Prove(x, w)) = 1] Prob[Verify(Prove(x,w))=1]足够低。
- Zero Knowledge:
- 给定证明者和验证者之间的交互,我们称这种交互为视图。
- 为了捕获零知识属性,使用多项式时间模拟器来生成模拟视图,该模拟器可以访问提供给验证者的相同输入(包括其随机性),但无法访问证明者的输入。
- 如果模拟视图与原始视图具有相同的分布,则我们说ZKP方案具有完全零知识。
- 如果这些分布在统计上接近,我们说ZKP方案具有统计零知识。如果这些分布没有多项式时间区分符,我们说ZKP方案具有计算零知识。
Zero knowledge range proofs
提交秘密的不同方式对应不同的ZKPR实现策略:
- 提交整数
- 平方分解。核心是将秘密元素分解为平方和。
- 基于签名的。以盲的方式证明prover知道一个关于秘密的签名。首先,区间内的所有元素都被签名,然后证明者知道签名的证据意味着这个整数属于预期的区间。
- 二进制表示
- 多基分解。
- 将秘密分解为bit表示:通过布尔运算证明它属于某个区间。
- 不是bit而是u进制表示:多基分解,允许构建对于小秘密情况下表现良好的ZKRP方案。
- 两层同态承诺。
- 关键思想是使用双线性配对对Pedersen承诺的向量进行承诺。
- 例如,给定配对 e : G 1 × G 2 → G 3 e: \mathbb G_1\times \mathbb G_2 → \mathbb G_3 e:G1×G2→G3和元素 v , u 1 , … , u N ∈ G 2 v,u_1,…,u_N ∈ \mathbb G_2 v,u1,…,uN∈G2,可以通过选择随机的 t ∈ G t ∈ \mathbb G t∈G并计算 C = e ( t , v ) ∏ i = 0 N e ( c i , u i ) C = e(t, v) ∏ᴺᵢ₌₀ e(cᵢ, uᵢ) C=e(t,v)∏i=0Ne(ci,ui)来对向量 [ c 1 , … , c N ] ∈ G 1 N [c_1,…,c_N] ∈\mathbb G_1^N [c1,…,cN]∈G1N进行承诺。
- Bulletproofs
- 以上提到的所有方案都依赖于一个可信的设置,这在加密货币的背景下可能不太理想。例如,如果对手能够规避这个可信设置,他将能够凭空创造货币。
- Bulletproofs的提出旨在通过使用内积证明实现ZKRP,并以非常小的证明大小为特点。
平方分解构造
实现Boudot于2001年提出的ZKRP所需的算法。这个构建过程需要一些基本组件,比如零知识证明两个承诺隐藏着相同的秘密,以及零知识证明秘密是一个完全平方数。
- 两个承诺隐藏相同秘密的零知识证明
P
K
S
S
=
{
x
,
r
1
,
r
2
∶
E
=
g
1
x
h
1
r
1
∧
F
=
g
2
x
h
2
r
2
}
PK_{SS} =\{x, r_1, r_2∶E = g_1^xh_1^{r_1} ∧ F = g_2^xh_2^{r_2}\}
PKSS={x,r1,r2∶E=g1xh1r1∧F=g2xh2r2}


g 1 D h 1 D 1 E − c = g 1 ω + c x h 1 η 1 + c r 1 g 1 − c x h 1 − c r 1 = Ω 1 g_1^Dh_1^{D_1}E^{-c}=g_1^{\omega+cx}h_1^{\eta_1+cr_1}{g_1^{-cx}h_1^{-cr_1}}=\Omega_1 g1Dh1D1E−c=g1ω+cxh1η1+cr1g1−cxh1−cr1=Ω1
- 秘密是一个完全平方数的零知识证明 P K S = x , r 1 ∶ E = g x 2 h r PKS = {x, r_1 ∶ E = g^{x^2} h^r} PKS=x,r1∶E=gx2hr

注意:
E
=
F
x
h
r
3
=
g
x
2
h
r
2
x
h
r
1
−
r
2
x
=
g
x
2
h
r
1
E=F^xh^{r_3}=g^{x^2}h^{r_2x}h^{r_1-r_2x}=g^{x^2}h^{r_1}
E=Fxhr3=gx2hr2xhr1−r2x=gx2hr1
调用的参数
g
1
=
F
,
h
1
=
h
2
=
h
,
g
2
=
g
g_1=F,h_1=h_2=h,g_2=g
g1=F,h1=h2=h,g2=g

- 一个秘密属于一个更大区间的零知识证明
P
K
L
I
=
{
x
,
r
∶
E
=
g
x
h
r
∧
x
∈
[
−
2
t
+
ℓ
b
,
2
t
+
ℓ
b
]
}
PK_{LI}= \{x, r ∶ E = g^xh^r ∧ x ∈ [−2^{t+ℓ}b, 2^{t+ℓ}b]\}
PKLI={x,r∶E=gxhr∧x∈[−2t+ℓb,2t+ℓb]}

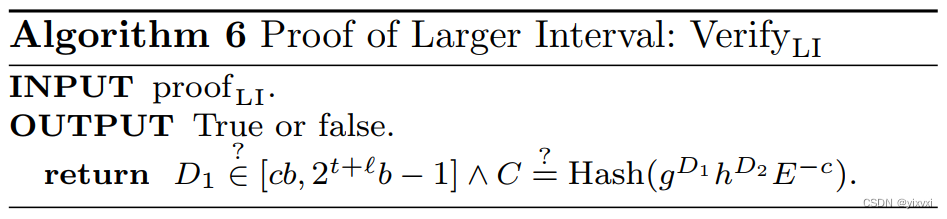
- a proof with tolerance
P
K
W
T
=
x
,
r
:
E
=
g
x
h
r
∧
x
∈
[
a
−
θ
,
b
+
θ
]
,
θ
=
2
t
+
l
+
1
b
−
a
PK_{WT} = {x, r :E = g^xh^r ∧ x ∈ [a − \theta, b + \theta]},\theta = 2^{t+l +1}\sqrt{b − a}
PKWT=x,r:E=gxhr∧x∈[a−θ,b+θ],θ=2t+l+1b−a


- Boudot在2001年提出的ZKRP方案。


Signature‑based construction\
- 成员关系证明
方案依赖于Boneh-Boyen数字签名:公私钥对
x
∈
R
Z
p
,
y
=
g
x
,
σ
=
g
1
/
(
x
+
m
)
x\in_R\mathbb Z_p,y=g^x,\sigma=g^{1/(x+m)}
x∈RZp,y=gx,σ=g1/(x+m),验证
e
(
σ
,
y
g
m
)
=
e
(
g
,
g
)
e(\sigma,yg^m)=e(g,g)
e(σ,ygm)=e(g,g)(q-Strong Diffie-Hellman assumption)

验证者最初为目标集合S中的每个元素计算数字签名。

证明者通过将其提升到随机选择的指数v ∈ ℤp对该数字签名进行盲化,使得确定签名的哪个元素是计算上不可行的。
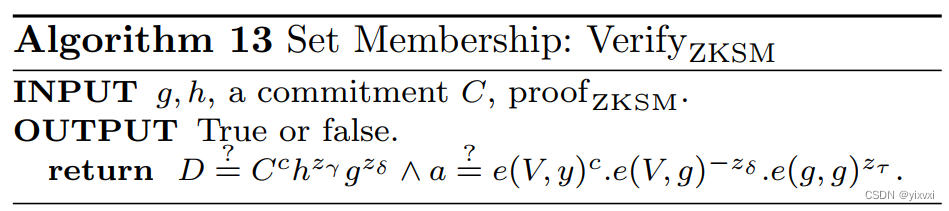
C
c
h
z
γ
g
z
δ
=
g
δ
c
h
γ
c
h
m
−
γ
c
g
s
−
δ
c
=
D
C^ch^{z_\gamma}g^{z_\delta}=g^{\delta c} h^{\gamma c}h^{m-\gamma c}g^{s-\delta c}=D
Cchzγgzδ=gδchγchm−γcgs−δc=D
这个是用挑战c和所使用的随机值生成的response
z
δ
,
z
γ
z_\delta,z_\gamma
zδ,zγ的验证
e
(
V
,
y
)
c
⋅
e
(
V
,
g
)
−
z
δ
⋅
e
(
g
,
g
)
z
τ
=
e
(
V
,
g
)
x
c
⋅
e
(
V
,
g
)
−
s
+
δ
c
⋅
e
(
g
,
g
)
t
−
τ
c
=
e
(
V
,
g
)
−
s
⋅
e
(
g
1
/
(
x
+
δ
)
,
g
)
τ
(
x
c
+
δ
c
)
⋅
e
(
g
,
g
)
t
−
τ
c
=
a
e(V,y)^c\cdot e(V,g)^{-z_\delta}\cdot e(g,g)^{z_\tau}=e(V,g)^{xc}\cdot e(V,g)^{-s+\delta c}\cdot e(g,g)^{t-\tau c}=e(V,g)^{-s}\cdot e(g^{1/(x+\delta)},g)^{\tau(xc+\delta c)}\cdot e(g,g)^{t-\tau c}=a
e(V,y)c⋅e(V,g)−zδ⋅e(g,g)zτ=e(V,g)xc⋅e(V,g)−s+δc⋅e(g,g)t−τc=e(V,g)−s⋅e(g1/(x+δ),g)τ(xc+δc)⋅e(g,g)t−τc=a
- Range proof
将秘密 δ \delta δ分解成以u为底
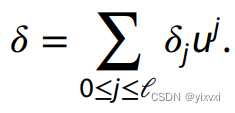
如果每个 δ j \delta_j δj 属于区间 [ 0 , u ) [0, u) [0,u),那么我们有 δ ∈ [ 0 , u ℓ ) \delta \in [0, u^\ell) δ∈[0,uℓ)。可以很容易地将ZKSM算法调整为执行此计算。



为了获得任意范围 [ a , b ) [a, b) [a,b) 的零知识范围证明,先证明 δ ∈ [ a , a + u ℓ ) \delta \in [a, a + u^\ell) δ∈[a,a+uℓ)和 δ ∈ [ b − u ℓ , b ) \delta \in [b - u^\ell, b) δ∈[b−uℓ,b),使用算法15两次。换句话说,需要证明 δ − b + u ℓ ∈ [ 0 , u ℓ ) \delta - b + u^\ell \in [0, u^\ell) δ−b+uℓ∈[0,uℓ)和 δ − a ∈ [ 0 , u ℓ ) \delta - a \in [0, u^\ell) δ−a∈[0,uℓ)。
Bulletproof
详见https://blog.csdn.net/jiongxv/article/details/124133111或原文