Project_Euler-11 题解

题目

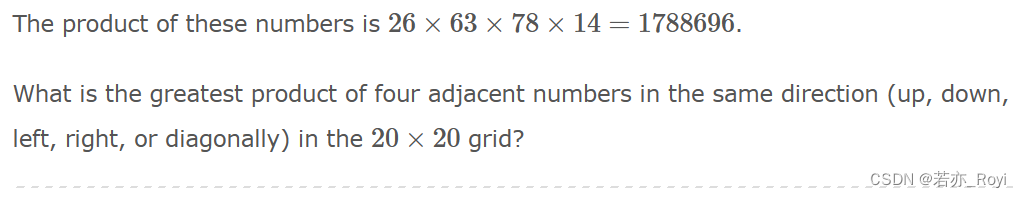
题目中给出的数据如下：

08 02 22 97 38 15 00 40 00 75 04 05 07 78 52 12 50 77 91 08
49 49 99 40 17 81 18 57 60 87 17 40 98 43 69 48 04 56 62 00
81 49 31 73 55 79 14 29 93 71 40 67 53 88 30 03 49 13 36 65
52 70 95 23 04 60 11 42 69 24 68 56 01 32 56 71 37 02 36 91
22 31 16 71 51 67 63 89 41 92 36 54 22 40 40 28 66 33 13 80
24 47 32 60 99 03 45 02 44 75 33 53 78 36 84 20 35 17 12 50
32 98 81 28 64 23 67 10 26 38 40 67 59 54 70 66 18 38 64 70
67 26 20 68 02 62 12 20 95 63 94 39 63 08 40 91 66 49 94 21
24 55 58 05 66 73 99 26 97 17 78 78 96 83 14 88 34 89 63 72
21 36 23 09 75 00 76 44 20 45 35 14 00 61 33 97 34 31 33 95
78 17 53 28 22 75 31 67 15 94 03 80 04 62 16 14 09 53 56 92
16 39 05 42 96 35 31 47 55 58 88 24 00 17 54 24 36 29 85 57
86 56 00 48 35 71 89 07 05 44 44 37 44 60 21 58 51 54 17 58
19 80 81 68 05 94 47 69 28 73 92 13 86 52 17 77 04 89 55 40
04 52 08 83 97 35 99 16 07 97 57 32 16 26 26 79 33 27 98 66
88 36 68 87 57 62 20 72 03 46 33 67 46 55 12 32 63 93 53 69
04 42 16 73 38 25 39 11 24 94 72 18 08 46 29 32 40 62 76 36
20 69 36 41 72 30 23 88 34 62 99 69 82 67 59 85 74 04 36 16
20 73 35 29 78 31 90 01 74 31 49 71 48 86 81 16 23 57 05 54
01 70 54 71 83 51 54 69 16 92 33 48 61 43 52 01 89 19 67 48

思路

首先将数据保存下来，这里选择开辟一个 $20+$ 的数组，通过重定向输入。

题目让我们寻找四个呈一直线（竖直、水平或对角线）相邻的数的乘积最大的值，我们可以维护一个方向数组，对于每个基准元素选择上、右上、右、右下四个方向分别计算每个方向上4个元素的乘积。

对于这个方向数组：
记录的是基准元素的偏移量。

int dir[4][2] = {
	// 上、    右上、  右、   右下
    {-1, 0},{-1, 1},{0, 1},{1, 1}
};

代码

#include <stdio.h>
#include <stdlib.h>
#include <math.h>
#include <string.h>
#include <time.h>
#define MAX_N 20

int gird[MAX_N + 5][MAX_N + 5];
int dir[4][2] = {
    {-1, 0},{-1, 1},{0, 1},{1, 1}
};

int calc(int x, int y) {
    int ans = 0;
    // 外层循环表示四个方向
    for (int k = 0; k < 4; k++) {
        int p = 1;
        // 内层循环表示偏移量
        // 这层代码的语义是：向k方向偏移step步后的元素值的记录
        for (int step = 0; step < 4; step++) {
            int dx = x + step * dir[k][0];
            int dy = y + step * dir[k][1];
            // 
            if (dx < 0 || dx >= MAX_N) break;
            if (dy < 0 || dy >= MAX_N) break;
            // 将这个记录保存
            p *= gird[dx][dy];
        }
        if (p > ans) ans = p;
    }
    return ans;
}

int main() {
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            scanf("%d", &gird[i][j]);
        }
    }

    int ans = 0;
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            int p = calc(i, j);
            if (p > ans) ans = p;
        }
    }
    printf("%d\n", ans);
    /*
    for (int i = 0; i < MAX_N; i++) {
        for (int j = 0; j < MAX_N; j++) {
            printf("%02d ", gird[i][j]);
        }
        printf("\n");
    }
    */
    return 0;
}