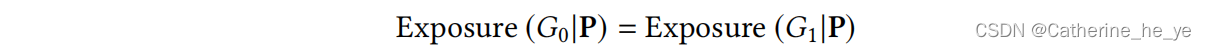在前面的章节里已经介绍过小波的理论、公式等知识点，现在我们来看看如何用小波来实现对复杂信号的成分分析。

在我们这个示例代码里，我们只使用到如下几个库：

import numpy as np
from matplotlib import pyplot as plt

首先创建一个包含多频率成分的信号

我们使用numpy和python来实现相关代码，并且所用的小波函数为墨西哥帽小波。于是我们可以得到下面这些代码：

# 创建信号和时间数组
num_samples = 1000
duration = 1.0
time = np.linspace(0, duration, num_samples)
signal = np.sin(2 * np.pi * 10 * time) + np.sin(2 * np.pi * 5 * time) + np.sin(2 * np.pi * 1 * time)

感兴趣的话，可以使用FFT工具对上述信号成分进行分析，其具体代码为：

# 对原始信号的频率进行分析
spectrum = np.fft.fft(signal) # 计算信号的频谱
freq = np.fft.fftfreq(signal.size, d=duration/num_samples) # 计算频率数组

# 绘制原始信号的频谱
plt.plot(freq, np.abs(spectrum))
plt.xlabel('Frequency')
plt.ylabel('Amplitude')
plt.show()

然后我们用数学实现一个墨西哥草帽小波

墨西哥草帽小波（Mexican Hat Wavelet）也叫Ricker小波，是一种常用的小波函数，其可以应用于信号处理、图像处理等领域。

它的数学公式为：

$$\varphi (t)=\frac{2}{\sqrt{3\sigma }{\pi }^{\frac{1}{4}}}(1-\frac{t^2}{{\sigma }^2})\cdot exp(\frac{-t^2}{2{\sigma }^2})$$

看起来挺复杂的，但是还可以进一步简化为：

$$\varphi (t)=(1-t^2)\ast exp(-t^2/2)$$

因为其他几项都是常熟C，所以我们可以直接隐去。然后就有如下实现公式：

def base_wavelet_ricker(frequency, num_samples, sampling_time=1.0):
    t = np.linspace(-sampling_time/2, sampling_time/2, num_samples)
    wavelet = (1.0 - 2.0 * np.pi**2 * frequency**2 * t**2) * np.exp(-np.pi**2 * frequency** 2 * t**2)
    return wavelet

然后我们开始对原始信号进行处理吧

# 分别使用1-16Hz的小波函数对信号进行小波变换
wavelets = []
for i in range(1, 17):
    wavelet = base_wavelet_ricker(i, num_samples, duration)
    wavelets.append(wavelet)

# 使用阈值法，对小波变换后的信号成分进行筛选
threshold = 0.5
results = []
for i in range(len(wavelets)):
    result = np.convolve(signal, wavelets[i], mode='same')
    result = np.convolve(result, wavelets[i], mode='same')
    result[np.abs(result) < threshold] = 0
    results.append(result)

接下来可以把信号成分进行绘制

接下来我们把处理后的数据按时间、频率、幅度进行绘制，因此得到所谓的三维 时频图。

# 创建三维坐标轴对象
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')

# 绘制小波时频图
X, Y = np.meshgrid(time, range(1, 17))
ax.plot_surface(X, Y, np.array(results), cmap='rainbow')

# 设置坐标轴标签
ax.set_xlabel('Time (s)')
ax.set_ylabel('Frequency (Hz)')
ax.set_zlabel('Amplitude')

# 显示图像
plt.show()

然后得到的显示结果如下：

现在我们看到，在对信号进行处理后，可以看到信号主要集中在0-5Hz，并且一直持续到10Hz左右都有信号分布。