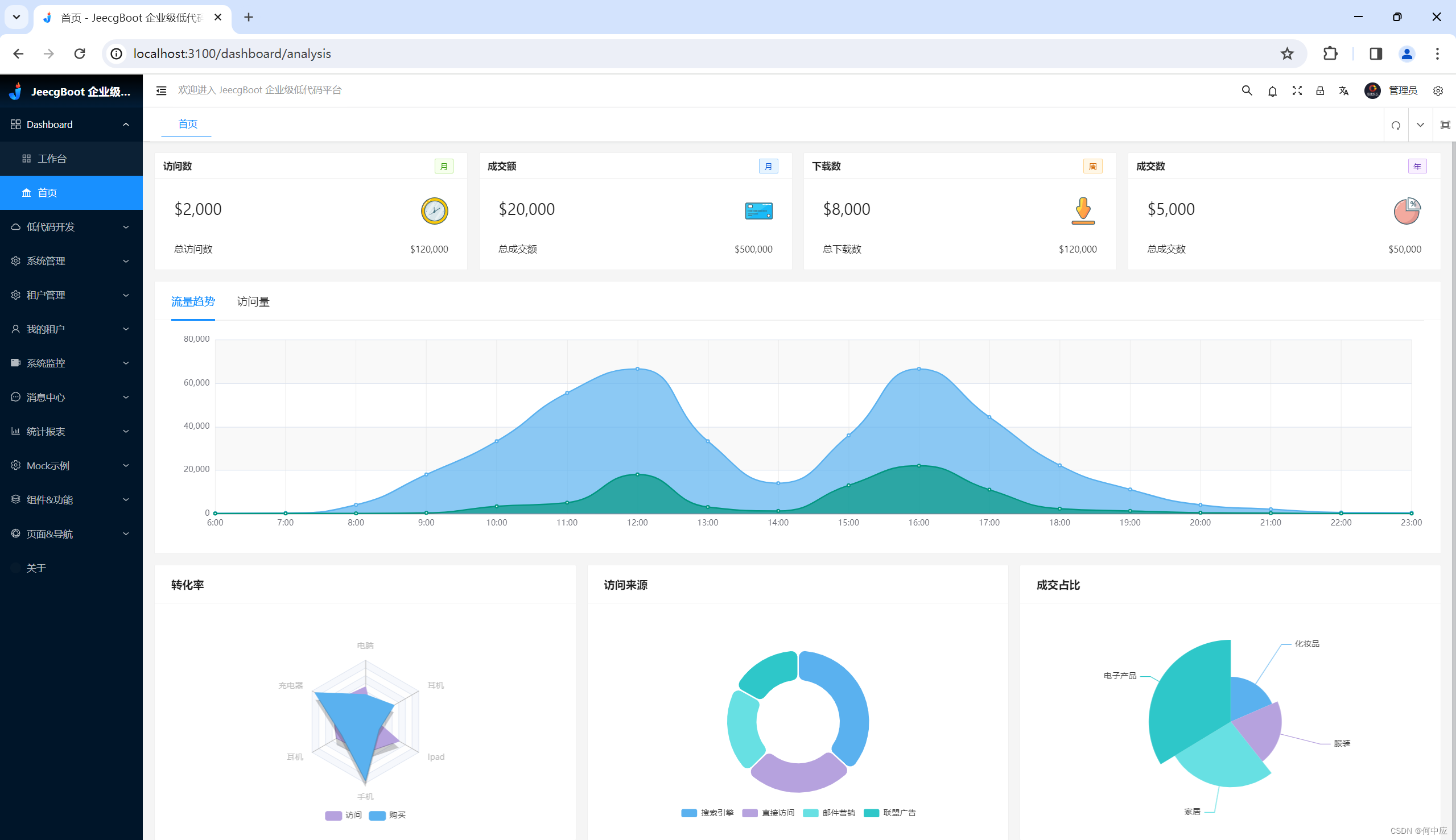
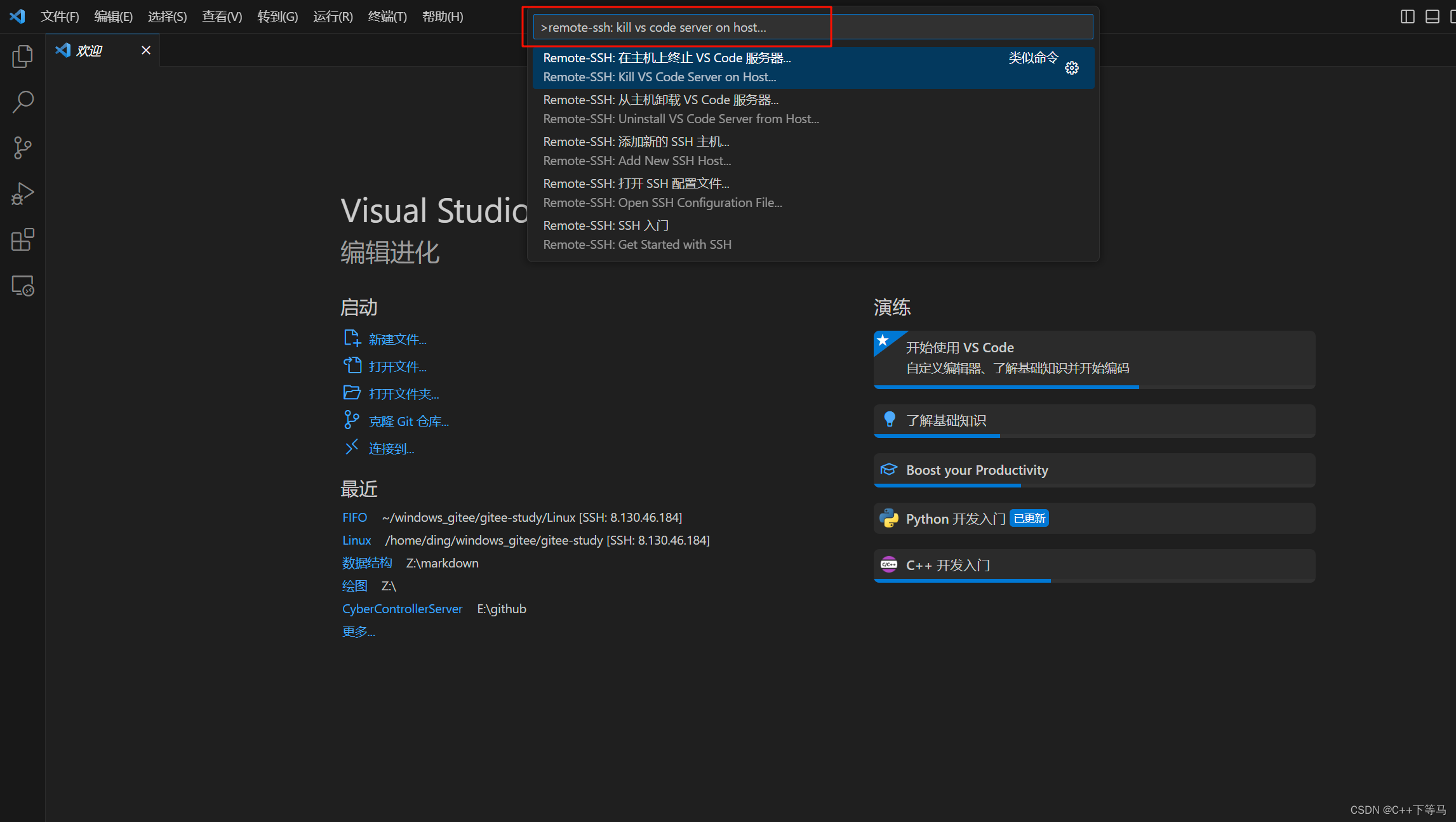
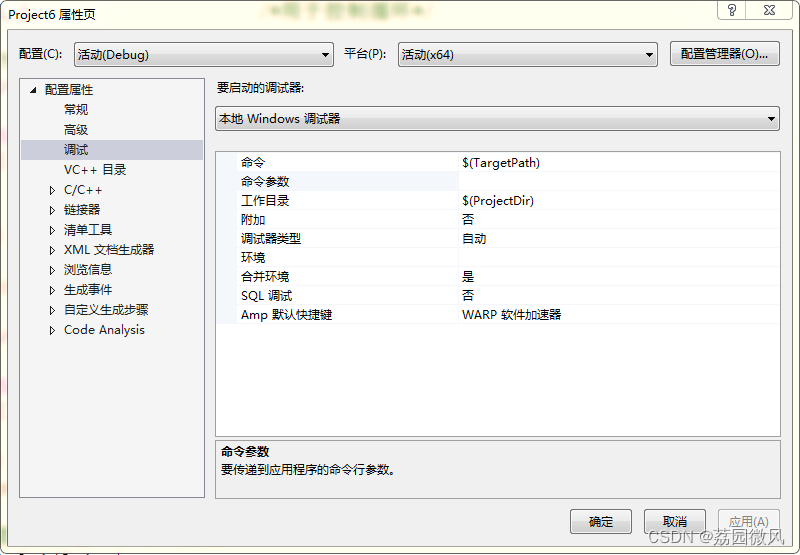
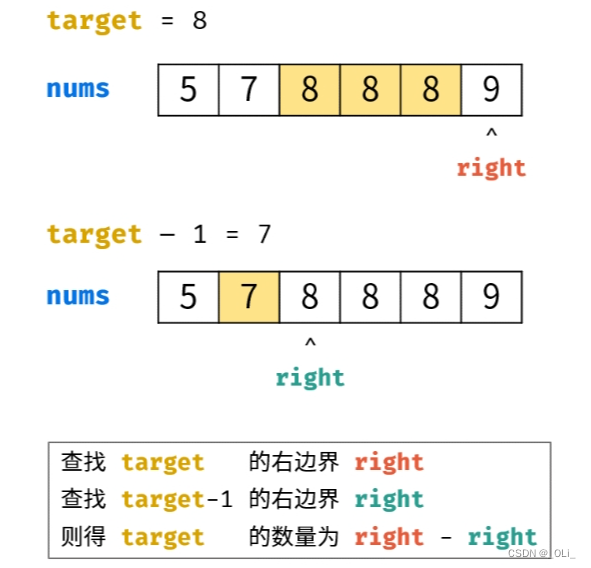
开始背包问题，掌握0-1背包和完全背包即可，注：0-1背包是完全背包的基础。

0-1背包问题：有n件物品和一个最多能背重量为w 的背包。第i件物品的重量是weight[i]，得到的价值是value[i] 。每件物品只能用一次，求解将哪些物品装入背包里物品价值总和最大。下面是n=4的例子：

如果用穷举方法，应该使用回溯法，那么每个物件都有放一个和不放两种选择，所以回溯的时间复杂度是O(2^n)，达到指数级。所以要使用动态规划。

以这个例题来进行二维dp数组和一维dp数组的动规五部曲：背包最大重量为4。物品为：

	重量	价值
物品0	1	15
物品1	3	20
物品2	4	30

问背包能背的物品最大价值是多少？
 

● 二维dp数组

1. 确定动规数组元素的含义。使用的是二维数组 dp[i][j]：从物品[0,i]范围内随便选择，放进容量为j的背包里，dp[i][j]是背包的最大价值。如下图所示：

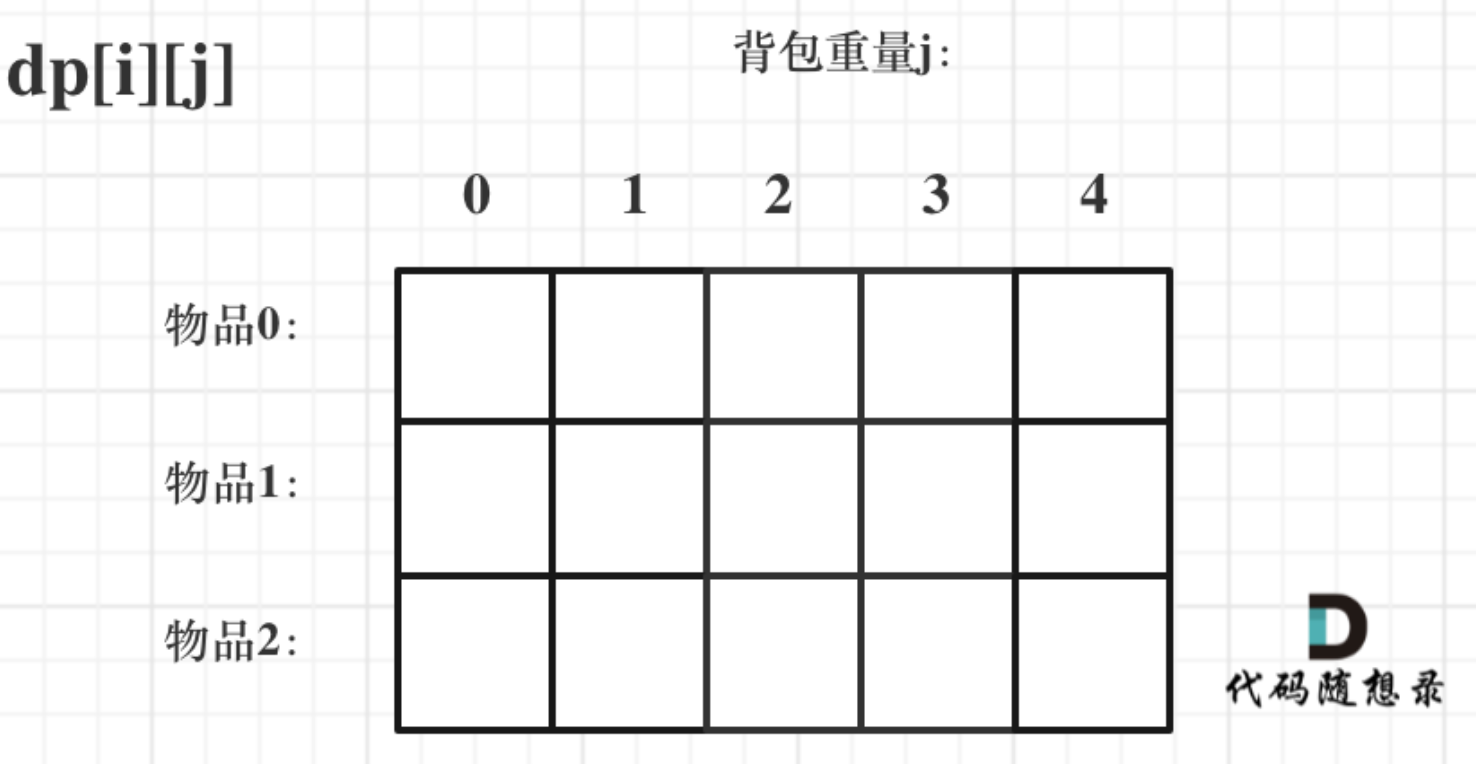
2. 确定递推公式。我们可以根据两种方式得到dp[i][j]，两种方式对应两种情况，其实dp[i][j]就是取这两种情况的最大值。

①不放物品 i。如果物品i放进重量为j的背包会超重，那么不能把i放进去，所以重量设定为j的话，从[0,i-1]选择和从[0,i]选择的最大价值是一样，所以 dp[i][j] = dp[i-1][j] 。

②放物品 i。如果不会超重，可以放进去。物品 i 放进去，背包最大重量为 j ，还没有放进去物品 i 的时候，背包的最大重量为 j - weight[i] ，数量为i-1，所以这时背包的最大价值为 dp[ i-1 ][ j - weight[i] ]。加入物品 i ，背包价值 dp[i][j] 就为 dp[ i-1 ][ j - weight[i] ] + value[i] 。

所以dp[i][j]= max ( dp[i-1][j] , dp[ i-1 ][ j - weight[i] ] + value[i] )。

必须牢记dp[i][j]的含义。

3. 如何初始化。

在上图里面，背包重量j为0的时候，什么也不能放进去，所以这一列肯定都是0。

物品 0 那一行，只能选择物品 0 自己，所以背包重量 j >=物品 0 的重量对应的表格都应该填上物品 0 的价值15.所以初始化后：

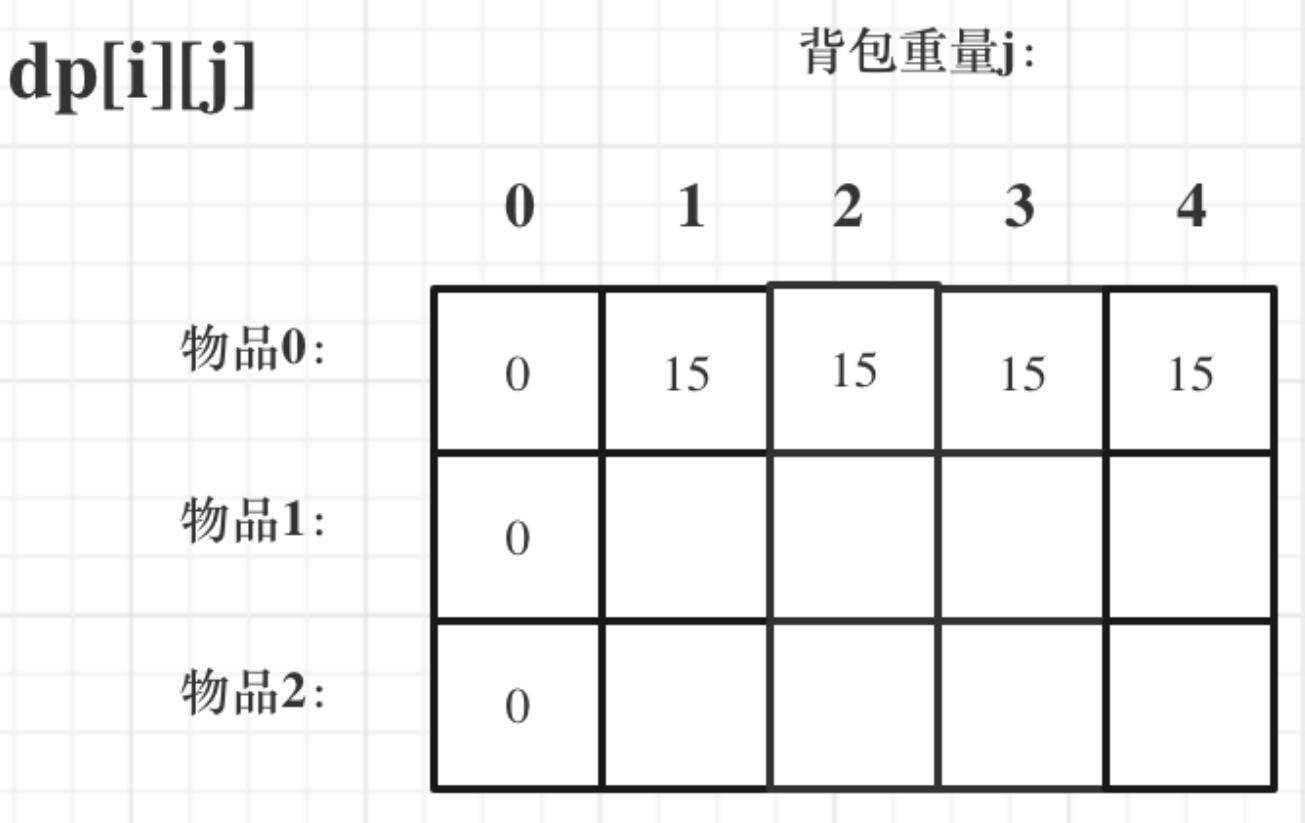
4. 遍历顺序。 根据上表，第一行第一列已经初始化，所以 i 应该从1到2，j 从 0 到背包容量4。是先行还是先列呢，其实都一样。先每个物品那一行统计完更好理解一些，但是先列也是从上往下走的，到一个元素的时候，左上角（包括正上方）的dp[i][j]都已经统计完成，所以都可以。背包问题里，两个for循环的先后循序是非常有讲究的。

5. 打印dp数组。

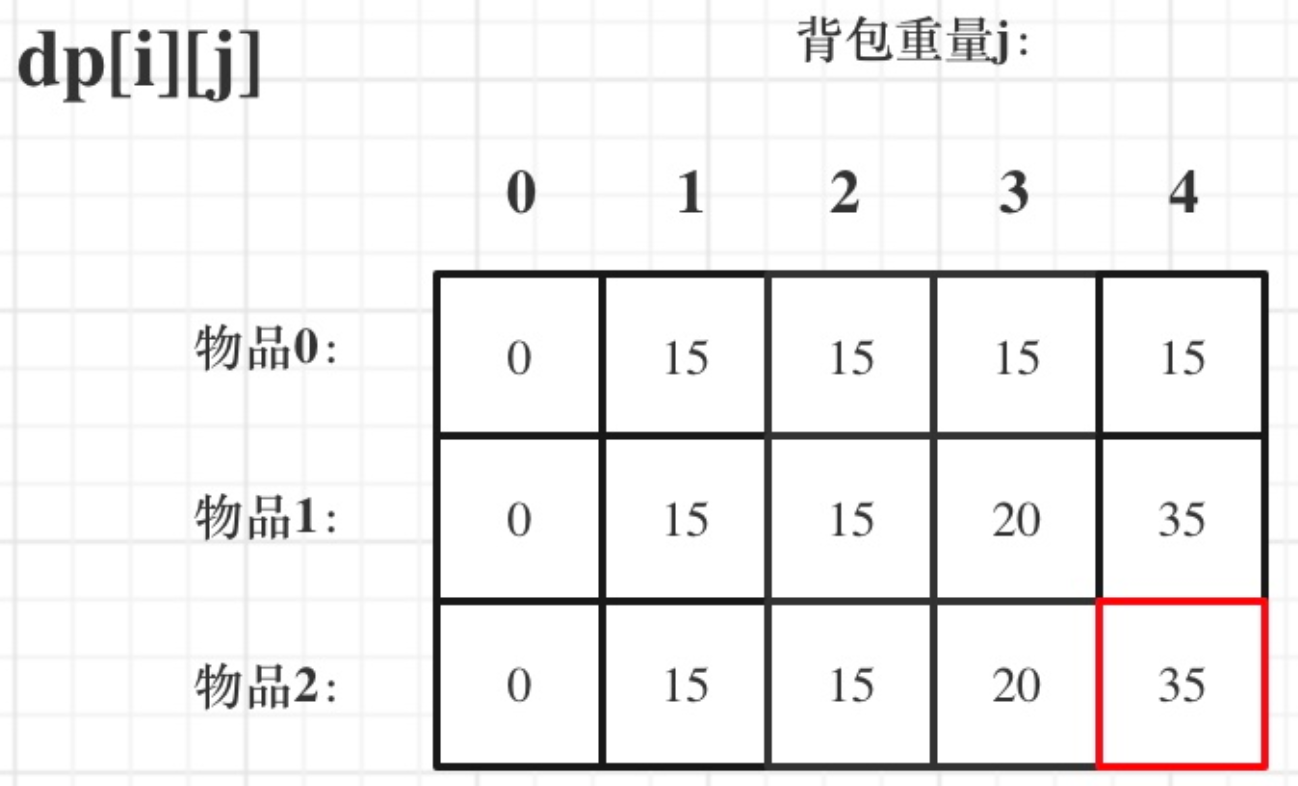
最后的结果就是返回dp[2][4]。

做题巩固一下：

题目链接46. 携带研究材料：题目链接

和上面例题的分析过程一样，使用二维dp数组，代码如下：

void maxValue(){
    int m,begweight;//M 代表物品的种类数，begweight是背包容量
    cin>>m>>begweight;
    vector<int> weight(m);
    vector<int> value(m);
    //读取重量和价值
    for(int i=0;i<m;++i){
        cin>>weight[i];
    }
    for(int i=0;i<m;++i){
        cin>>value[i];
    }
    //注意行列数
    vector<vector<int>> dp(m,vector<int>(begweight+1,0));
    //初始化
    for(int j=0;j<m;++j){
        dp[j][0]=0;
    }
    for(int j=weight[0];j<=begweight;++j){
        dp[0][j]=value[0];
    }
    //递推
    for(int i=1;i<m;++i){
        for(int j=1;j<=begweight;++j){
            //物品i重量超过背包容量，肯定不放进去
            if(j<weight[i]) dp[i][j]=dp[i-1][j];       
            //物品i重量小于背包容量，也不一定能放进去，取max
            else dp[i][j]=max(dp[i-1][j],dp[i-1][j-weight[i]]+value[i]);
        }
    }
    cout<< dp[m-1][begweight] << endl;
}

● 一维滚动数组 

在上面使用二维数组的时候，递推公式：dp[i][j] = max(dp[i - 1][j], dp[i - 1][j - weight[i]] + value[i]);所以dp[i-1]这一层的得到之后，就拷贝到对应的dp[i]这一层来（dp[i]左上方的dp[i-1]肯定都已经得到），这个递推公式可以把 dp[ i-1] 的都改为dp[ i ]：

dp[ i ][ j ] = max(dp[ i ][ j ], dp[ i ][ j - weight[ i ] ] + value[ i ]);

与其把dp[i - 1]这一层拷贝到dp[i]上，不如只用一个一维数组了，只用dp[j]（一维数组，也可以理解是一个滚动数组，只留下了上面二维数组的列）。

动规五部曲分析如下：

1. dp[j]含义。含量是j的背包能装下的最大价值。可以从所有的物品中选择。

2. 递推公式。其实和二维数组是差不多的意思，两种情况：放 i 和不放 i 。dp数组省略了i所以这个递推公式也去掉i：dp[ j ] = max(dp[ j ], dp[ j - weight[ i ] ] + value[ i ]);

3. 初始化。只能确定含量是0的背包装下的价值是0，所以dp[0]=0。其他的不能确定，都初始化为0。

4. 遍历顺序。在上面说到：背包问题里，两个for循环的先后循序是非常有讲究的。在这里也体现出来。二维的时候，先背包或者先物品都可以，但是一维的时候，只能先物品再背包，而且背包还得倒序遍历。

为什么背包是倒序遍历？倒序遍历是为了保证物品i只被放入一次。比如上面的例题，物品0的重量weight[0] = 1，价值value[0] = 15。第一轮i=0：先算dp[1]=max(dp[1],dp[0]+15)=15，那么dp[2]=max(dp[2] , dp[1] + 15)=30，dp[2]就包含了2个物品0。肯定是错的。那么考虑反过来，先算dp[4]的话，先算dp[4]=max(dp[4],dp[3]+15)=15，dp[3]=max(dp[3],dp[2]+15)=15，没有重复包含。所以只能倒序遍历。所以倒序遍历的原因是，本质上还是一个对二维数组的遍历，只不过第二行的覆盖第一行，第三行的覆盖第二行……并且右下角的值依赖上一层左上角的值，因此需要保证左边的值仍然是上一层的，从右向左覆盖。从左到右覆盖左边的值就是这一层更新过的了。

为什么只能先物品再背包？还是那句话：一维遍历本质上还是一个对二维数组的遍历，右下角的值依赖上一层左上角的值，所以需要保证左边的值仍然是上一层的，结合上面的背包倒序遍历，想象这个过程中，dp数组倒序遍历一轮就是更新了之前二维数组的一行，然后下一轮就是更新二维数组的下一行，这样左边的值仍然是上一层的。

如下图。既然没有了i，那么进行第二轮的j=4,j=3的时候，之前一轮的这两个值就会被覆盖，只有以“先物品再背包，背包倒序遍历”这个顺序来才能使得dp[j]和二维的dp[i-1][j]是一样的效果，我需要用到的是前一轮的值，那么不能先更新前一轮的值，而是要从后往前更新。所以除了这个情况之外的，都会覆盖原来左上角的值，是不对的。

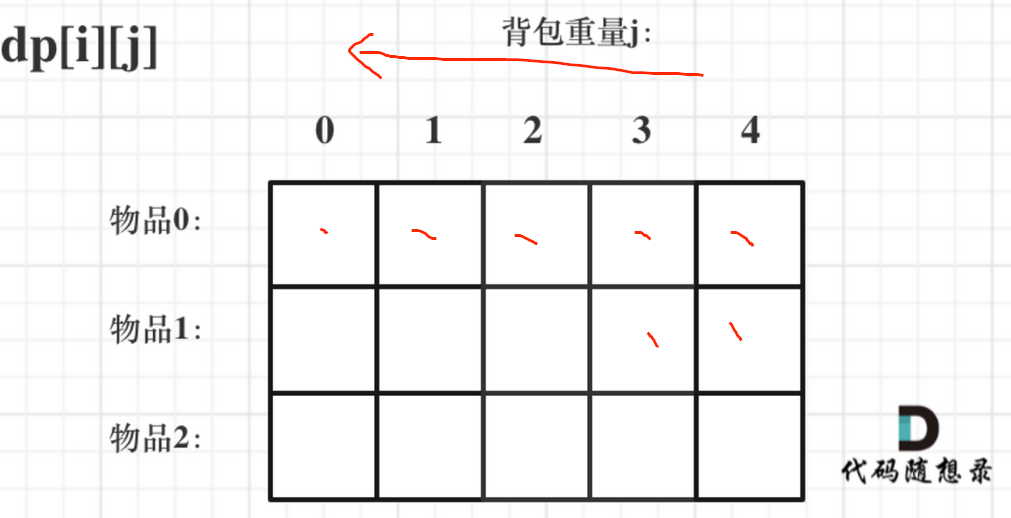
二维数组的时候，本来就是由上一层的dp[i-1]计算得到的，所以上一层的值直接能拿来用不会被覆盖，所以先物品先背包都可以。

背包循环里面，j<nums[i]的dp[j]保持以前的值，和二维的dp[i][j]=dp[i-1][j]对应，所以是判断条件。

5.打印。

代码如下：

void maxValue(){
    int m,begweight;//M 代表物品的种类数，begweight是背包容量
    cin>>m>>begweight;
    vector<int> weight(m);
    vector<int> value(m);
    for(int i=0;i<m;++i){
        cin>>weight[i];
    }
    for(int i=0;i<m;++i){
        cin>>value[i];
    }
    vector<int> dp(begweight+1,0);
    //初始化
    dp[0]=0;
    //递推,特别注意物品背包的顺序和背包循环内的顺序
    for(int i=0;i<m;++i){
        for(int j=begweight;j>=weight[i];--j){
            dp[j]=max(dp[j],dp[j-weight[i]]+value[i]);
        }
    }
    cout<< dp[begweight] << endl;
}

● 416. 分割等和子集

只要找到一个子集，这个子集的和是sum / 2即可，sum是n个数之和。是奇数可以直接返回false。

怎么转换成01背包问题？背包含量begweight是sum/2，n件物品——n个数；重量weight数组——n个数的值；价值value数组——n个数的值；只要背包最后在n个数中找到的子集的和（最大价值）是sum/2，返回true。

代码如下：

class Solution {
public:
    bool canPartition(vector<int>& nums) {
        int sum = 0;
        for(int a:nums)sum+=a;
        if(sum%2==1)return false;
        int begweight=sum/2;    //背包容量
        vector<int> dp(begweight+1,0);
        for(int i=0;i<nums.size();++i){ //注意nums.size()和begweight别弄混
        //j<nums[i]的dp[j]保持以前的值，和二维的dp[i][j]=dp[i-1][j]对应
            for(int j=begweight;j>=nums[i];--j){    
                dp[j]=max(dp[j],dp[j-nums[i]]+ nums[i]);
            }
        }
        //最后结果等于begweight(即sum/2)，找到
        if(dp[begweight]==begweight)return true;
        return false;
    }
};