文章目录
- Graph-based SLAM
- 数学概念
- 非线性最小二乘(Non-Linear Least Square)
- 解决的问题
- 误差函数
- 线性化
- 流程
- 非线性最小二乘在SLAM中的应用
- 图的构建(SLAM前端)
- 误差函数
- 误差函数的线性化
- 固定坐标系
- 构建线性系统
- 求解
- Cartographer介绍
Graph-based SLAM
数学概念
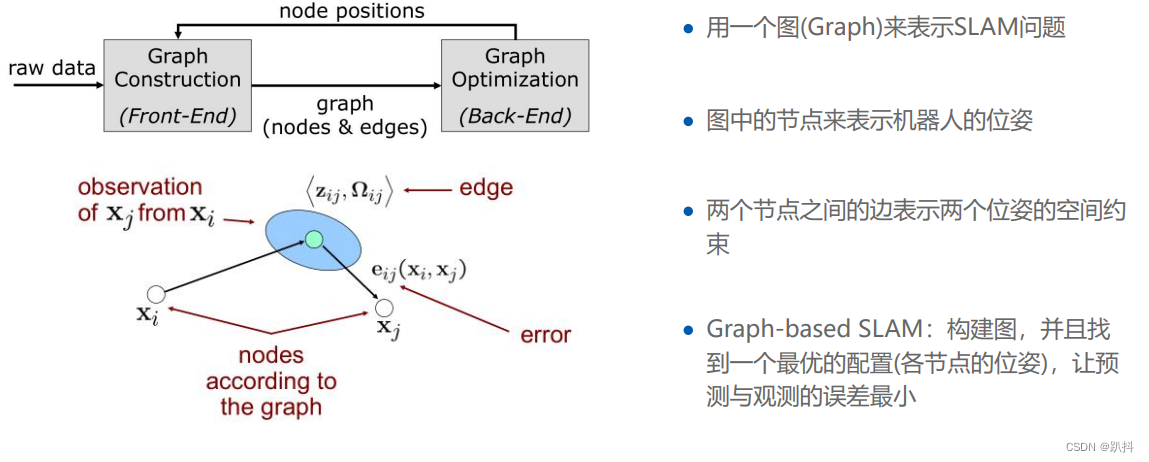
非线性最小二乘(Non-Linear Least Square)
解决的问题
- 给定一个系统,其状态方程由
f(x) = z描述。其中:- x为该系统的状态向量——即需要估计的值(在激光SLAM中就是机器人的位姿)
- f(x)是一个非线性的映射函数
- 状态向量x,可以通过非线性函数f(x)映射得到z,此时的z为预测得到
- z表示系统的可观值,可以通过传感器进行直接观测
- 给定该系统的n个混有噪声的观测值(z1,…,zn),估计状态向量x,使得其经过f(x)映射之后的预测值和观测值的误差最小
- 跟非线性最小二乘基本相同,不同之处在于f(x)是一个非线性函数

误差函数
目标为最小化预测和观测的差,因此误差即为预测和观测的差:

假设误差服从高斯分布,因此其对应的信息矩阵为Σi,即观测值的可靠性。如果越信任该观测值,Σ就越大,则E就越大,越优先最小化这个误差。则因此该观测值误差的平方定义为:
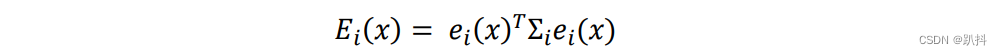
每一个观测值都有不同的可靠性,因此我们实际上采用加权最小二乘,对每一个误差项我们都有一个权重矩阵(即信息矩阵)来进行加权。所以非线性最小二乘的目标函数为:

直接想法: 求F(x)关于变量x的导数,令其等于0,求解方程即可。
对于线性问题,该方法可以正确,但是对于非线性问题不正确。因此,对于F(x)这样关于x的非线性方程。我们使用泰勒展开对其线性化。
线性化
F(x)是关于x的非线性函数的原因是,误差函数ei(x)是一个非线性函数。因此直接对误差函数ei(x)进行线性化即可:
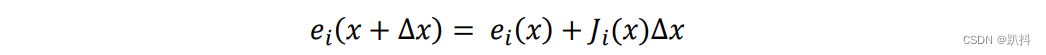
其中J为映射函数对状态向量x的导数,称之为Jacobian矩阵:
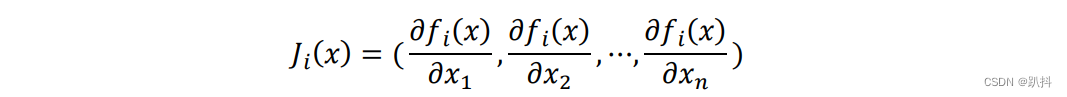
因此函数F(x)的可化解为:
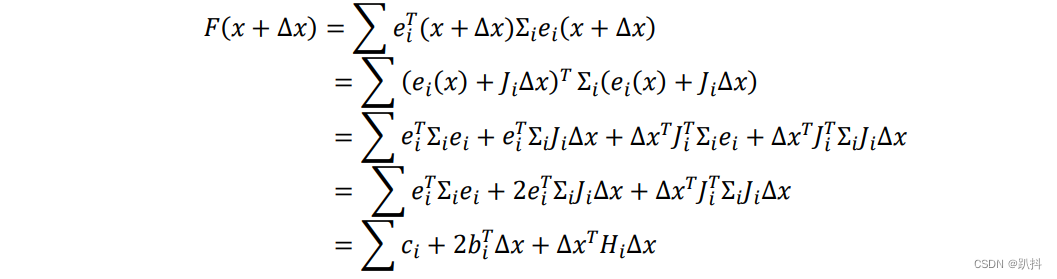
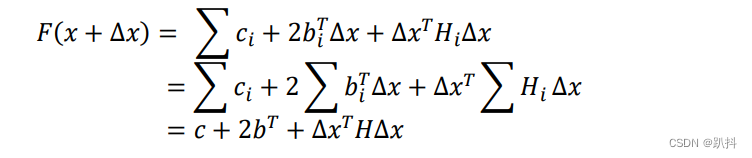
F(x+Δx)为关于变量∆x的二次函数,其极值可通过令其关于∆x的导数等于0求解得到:
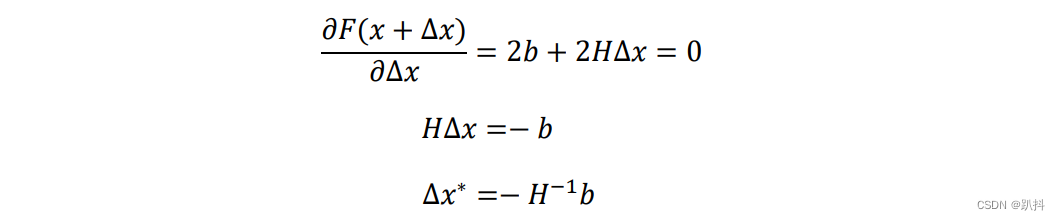
令x = x + ∆x,然后不断迭代,直至收敛即可。
流程
-
线性化误差函数:
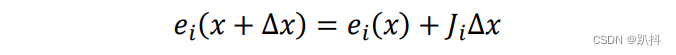
-
构建线性系统:

-
求解线性系统:
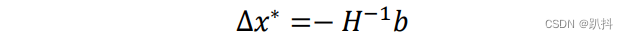
-
更新解,并不断迭代直至收敛:
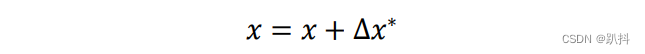
非线性最小二乘在SLAM中的应用
图的构建(SLAM前端)
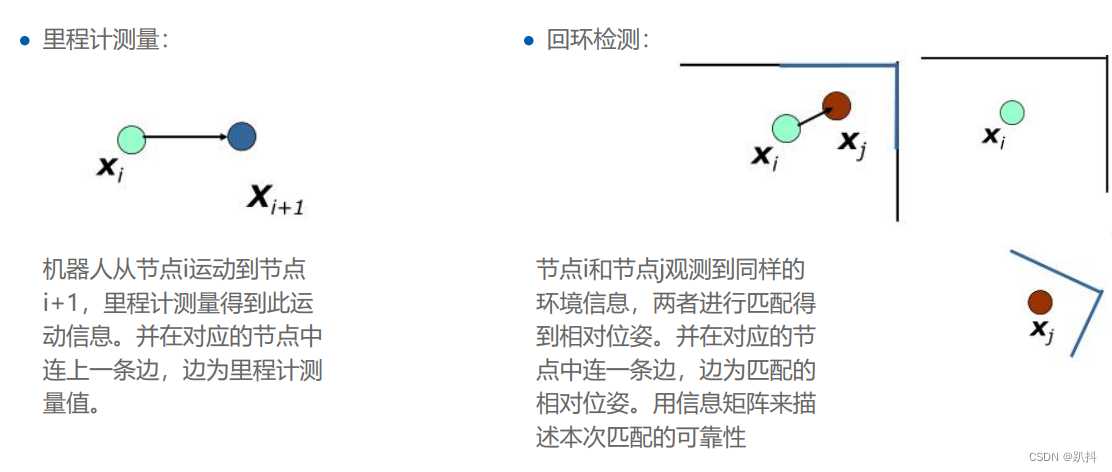
误差函数


误差函数的线性化

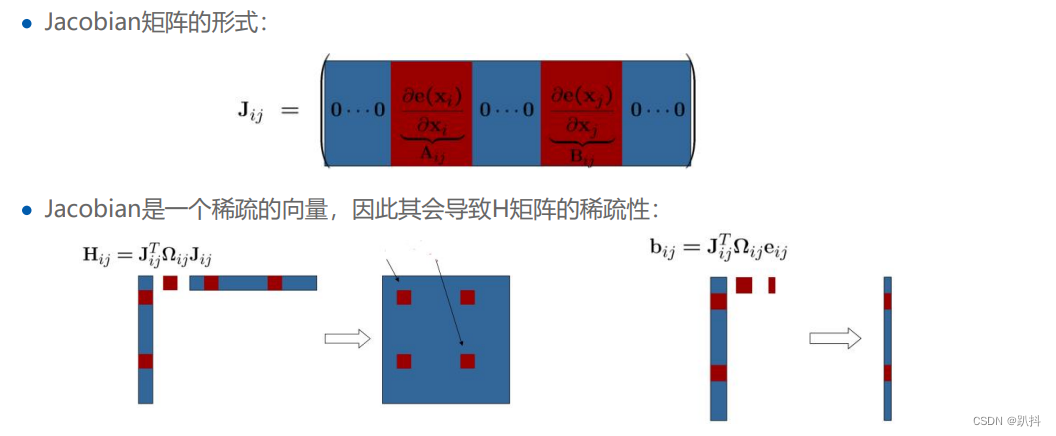
固定坐标系
观测值观测到的值两个位姿之间的相对位姿。但是满足相对位姿约束的解有无穷多组。为了让解唯一,必须加入一个约束条件让某一个位姿固定,一般选择第一个位姿,即:
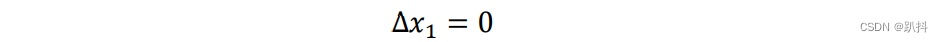
等价于加入的约束为:
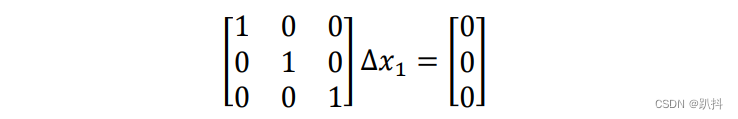
求解的线性系统为:
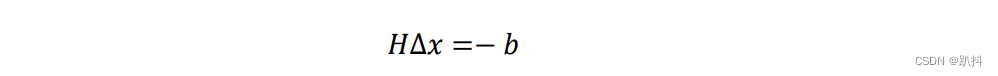
因此等价于:
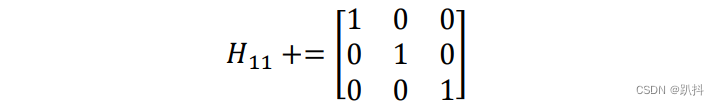
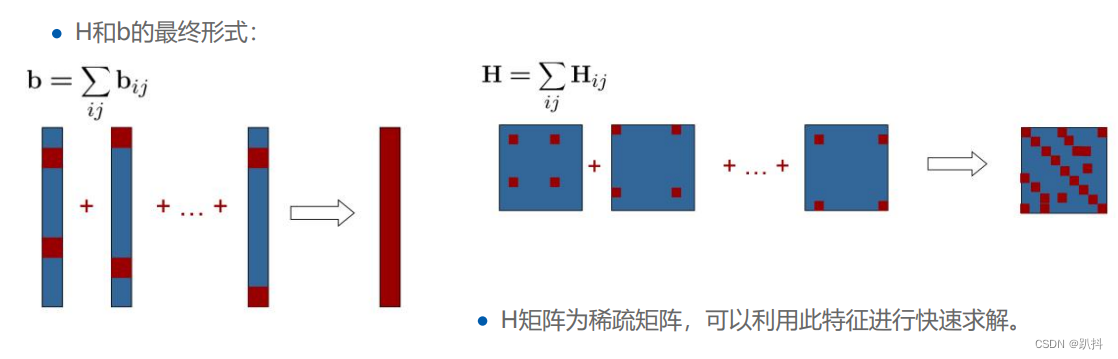
构建线性系统
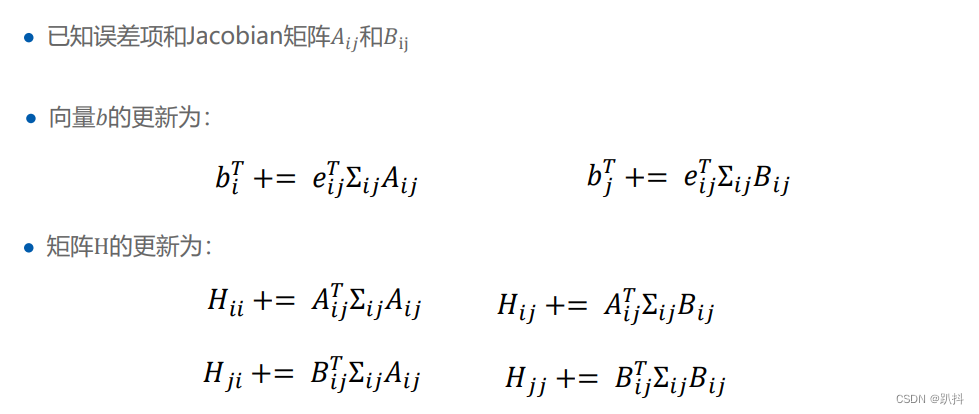
求解

Cartographer介绍
- 基于图优化的SLAM算法
- 比较完善的匹配系统,包含建图和定位
- 目前效果最好的开源激光SLAM系统
- 有人在专门的维护,不断增加新的特性