递归与回溯（一）

news2024/11/6 7:24:27

递归

递归一定要有出口，不然会无限调用，死循环

string fun(int n){
    if(n==0)
        return "a";
    if(n==1)
        return "b";
    return fun(n - 1) + fun(n - 2);
}

输出前8种结果：

在这里插入图片描述

双写数字递归例子

注意递归的return

int doubleNum(int n){
    if (n < 10){
        return (10 * n) + n;
    }
    else{
        int a = doubleNum(n / 10);
        int b = doubleNum(n % 10);
        return (100 * a) + b;
    }
}

以：1987为例说明递归顺序，由于每次递归都copy一次函数副本，只有return,才能结束递归的调用。

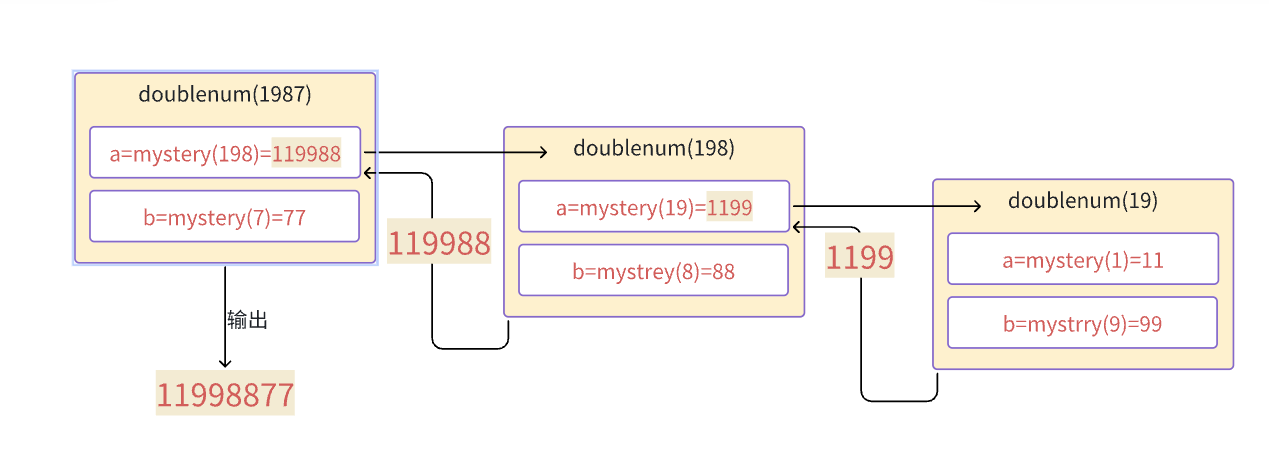
在这里插入图片描述

例子2,不管是谁递归，大小以递归数字为准

string func(string s){
    if (s.size()==1){
        return s+=s;//双写
    }
    else{
        string a = func(s.substr(1));//去掉第一个字母
        string b = func(s.substr(0,s.size()-1));//去掉最后一个字母
        return a+b;
    }
}

func(“abc”)结果是：ccbbbbaa

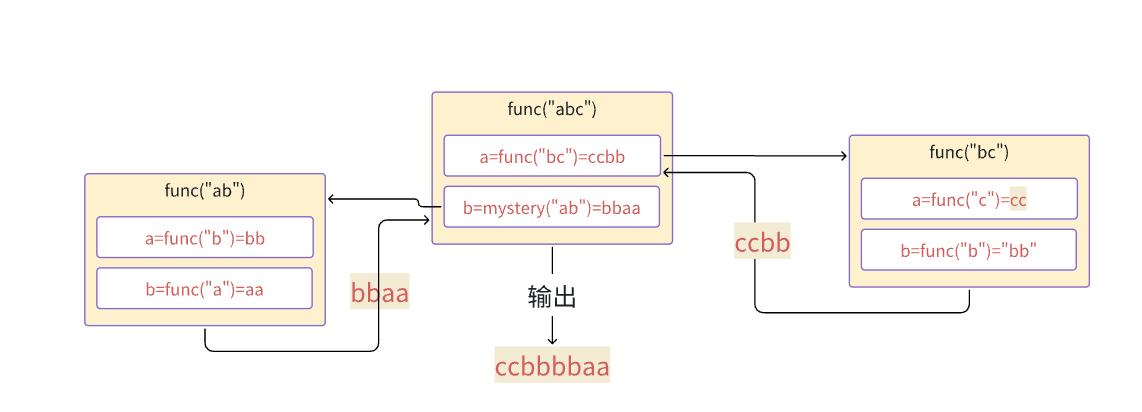
在这里插入图片描述

递归判断回文串

bool ishuiwen(string s){
    //最基本情况，递归出口
    if (s.size()<=1){//s是单个字符或者空，是回文
        return true;
    }
    else{
       char first = s[0];
       char last = s[s.size() - 1];
       //middle是去掉首位两字符的字符串
       string middle = s.substr(1, s.size() - 2);
       return (first == last && ishuiwen(middle));
    }

打印所有二进制

也就是给定数字n,打印出n的所有可能二进制排列

比如：

n=1 — 0,1

n=2 — 00,01;10,11

n=3 —000,001,010,011;100,101,110,111

…

发现规律：
n=1  {0},{1}
n=2  {00},{01};
     {10},{11}
n=3  {000},{001},{010},{011}
     {100},{101},{110},{111}
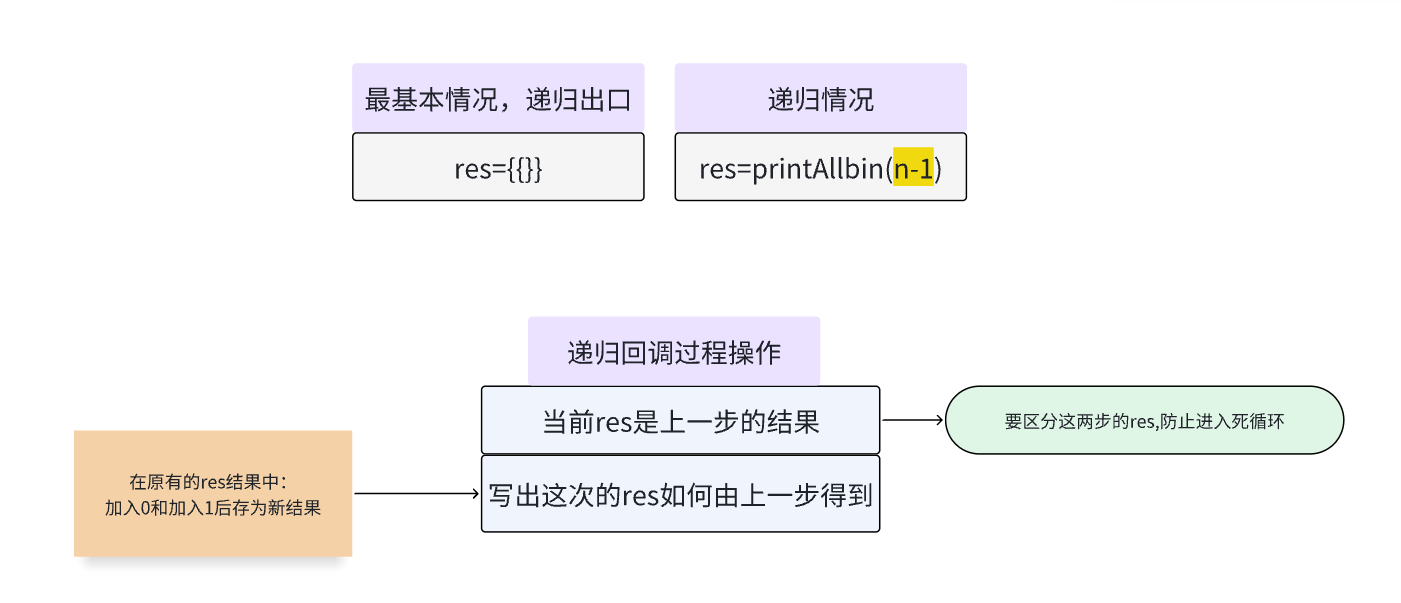
---所以后一个是前一个所有可能分别加上0和1构成新集合
---也就是n=4是n=3的所有结果，分别插入0和1
n=4
{0 000},{0 001},{0 010},{0 011},{0 100},{0 101},{0 110},{0 111}
{1 000},{1 001},{1 010},{1 011},{1 100},{1 101},{1 110},{1 111}

解：

vector<vector<int> > printfAllBin(int n){
    //base case,递归结束
    if(n==0)  return {{}};
    //递归求结果
    vector<vector<int>> res=printfAllBin(n-1);
    //对上一步进行操作得到下一步
    //这里是对当期的二进制结果前，加0或加1然后存储新结果
    int size = res.size();//这个是循环结束标志，每次递归res的大小都不同
    for (int i = 0; i < size;i++){
        auto tmp = res[i];
        tmp.push_back(0);//加0
        res.push_back(tmp);
        //加一
        res[i].push_back(1);
    }
    return res;
}

在这里插入图片描述

vector<vector<int> > printfAllBin(int n){
    //base case,递归结束
    if(n==0)  return {{}};
    //递归求结果
    vector<vector<int>> res;
    vector<vector<int>> cur= printfAllBin(n - 1);
    //cur作为当前res,更新下一次res
    for(auto& val:cur){
        //记录val值后加入1
        auto tmp = val;
        tmp.push_back(1);
        //原有val值加0
        val.push_back(0);
        //把结果都装入res中
        res.push_back(tmp);
        res.push_back(val);
    }
    return res;
}

这里用cur记录当前递归结果，然后加入0和1后，放入res中

子集和问题

78. 子集

求1个数组的子集和

以1，2，3为例

顺着思想 f ： \text{顺着思想}f\text{：} 顺着思想f：

f ( { } ) = { } f\left( \left\{ \right\} \right) =\left\{ \right\} f({})={}

f ( { 1 } ) = f ( { } ) + 1 = { } ， { 1 } f\left( \left\{ 1 \right\} \right) =f\left( \left\{ \right\} \right) +1=\left\{ \right\} \text{，}\left\{ 1 \right\} f({1})=f({})+1={}，{1}

f ( { 1 , 2 } ) = f ( { 1 } ) + 2 = { } , { 1 } , { 2 } , { 1 , 2 } f\left( \left\{ 1,2 \right\} \right) =f\left( \left\{ 1 \right\} \right) +2=\left\{ \right\} ,\left\{ 1 \right\} ,\left\{ 2 \right\} ,\left\{ 1,2 \right\} f({1,2})=f({1})+2={},{1},{2},{1,2}

f ( 1 , 2 , 3 ) = f ( { 2 } ) + 3 = { } , { 1 } , { 2 } , { 1 , 2 } , { 3 } , { 1 , 3 } , { 2 , 3 } , { 1 , 2 , 3 } f\left( 1,2,3 \right) =f\left( \left\{ 2 \right\} \right) +3=\left\{ \right\} ,\left\{ 1 \right\} ,\left\{ 2 \right\} ,\left\{ 1,2 \right\} ,\left\{ 3 \right\} ,\left\{ 1,3 \right\} ,\left\{ 2,3 \right\} ,\left\{ 1,2,3 \right\} f(1,2,3)=f({2})+3={},{1},{2},{1,2},{3},{1,3},{2,3},{1,2,3}

也就是 f ( { 1 , . . , n } ) = f ( { 1 , . . , n − 1 } ) ∪   f ( { 1 , . . , n − 1 } ) 的每一个子集加n \text{也就是}f\left( \left\{ 1,..,n \right\} \right) =f\left( \left\{ 1,..,n-1 \right\} \right) \cup \ f\left( \left\{ 1,..,n-1 \right\} \right) \text{的每一个子集加n} 也就是f({1,..,n})=f({1,..,n−1})∪ f({1,..,n−1})的每一个子集加n

正向解法：

 vector<vector<int>> subsets(vector<int>& nums) {
        // f({1,..n})=f({1,..,n-1}) U f({1,..,n-1})+n
        vector<vector<int>> res({{}});
        for(int i=0;i<nums.size();i++){
            int n=res.size();//----这个n很重要，限定了当前res的增长
            for(int j=0;j<n;j++){
                //现有元素装入res
                res.push_back(res[j]);
                //res元素都加上nums[i]
                res[j].push_back(nums[i]);
            }
        }
        return res;
    }

递归做法：

一个典型的递归结构:

  • [1,2,3] 的子集可以由 [1,2] 追加得出，[1,2] 的子集可以由 [1] 追加得出

  • base case 显然就是当输入集合为空集时，输出子集也就是一个空集。

  • 递归出口是：{{}}—这里是vector<vector<>>

  • 解题关键就是：当前子集和=上一个子集和∪{上一个子集加上多出的元素}

  • 也就是：每次从尾部取出一个元素，然后计算当前子集和和该元素的情况

    思维如下：

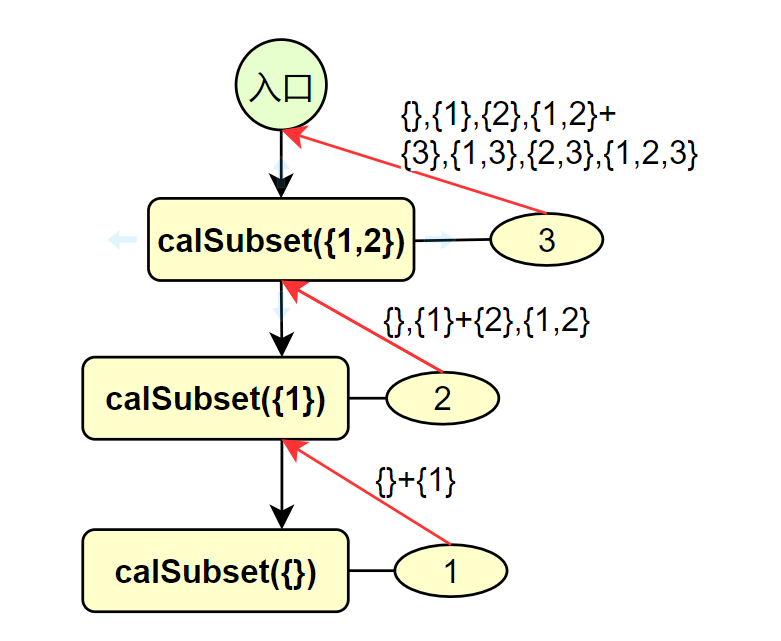
在这里插入图片描述

vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        //递归出口
        if(nums.size()==0)   return {{}};
        //从尾部减少一个元素
        int x=nums.back();
        //减少元素后的集合
        auto set=nums;
        set.pop_back();//去掉元素
        /*当前子集和元素*/
        for(auto& val:subsets(set)){
            vector<int> choose_cur =val;
            choose_cur.push_back(x);
            //res加入选它的和原来的（不选）
            res.push_back(val);
            res.push_back(choose_cur);
        }
        return res;
    }

vector<vector<int>> subsets(vector<int>& nums) {
        vector<vector<int>> res;
        //递归出口
        if(nums.size()==0) return {{}};
        //每次去掉nums前面元素
        int x=nums.front();
        nums.erase(nums.begin());//去掉x
        //记录递归子集
        vector<vector<int>> set=subsets(nums);
        //回退中：前一个生成后一个的操作
        for(auto& val:set){
            auto tmp=val;
            tmp.push_back(x);
            //res插入两种情况
            res.push_back(val);//不选择x
            res.push_back(tmp);//选择x
        }
        return res;
    }

subsets(set)需要新的变量，不可以直接用res,因为auto遍历，res有push_back操作，会造成死循环

每次从nums去掉前一个或后一个都可以，只要能生成待插值即可

全排列问题

在这里插入图片描述

和前面类似，后面的也可以由前面的生成，规律就是：每一个元素插空

比如对d,其中一个子集{c,b,a}中:
                __c__b__a__,d可以选择__任一处
所以：4乘以{a,b,c}的6种情况，4！=24

难点在于：前一个到后一个的插空

思路：首先原有的一个，直接在最前面插作为结果

​ 然后接下来，从最后一个开始遍历当前字符串，每次插入x后作为结果保存在res中

在这里插入图片描述

  • 首先先看一个插值方法
void traverse(const vector<vector<int>>& res){
    for(auto aa:res){
        for(auto bb:aa){
            cout << bb << " ";
        }
        cout << endl;
    }
}
int main(){
    vector<int> nums = {1, 2, 3, 4, 5};
    vector<vector<int>> res;
    for (auto it = nums.begin();it<=nums.end();it++){
        //mm在it位置插入6，此时it指向了新值
        it = nums.insert(it, 6);
        //mm放入res
        res.push_back(nums);//（6）,5,1,2,3,4
        //mm删除插入新值，不影响下一个插入
        it=nums.erase(it);//it回到原来的1
    }
    traverse(res);
    return 0;
}

在这里插入图片描述

巧用erase和insert，但是记住返回值是下一个迭代器

本题解法：

vector<vector<int>> fullLine(const vector<int>& nums){
    vector<vector<int>> res;
    if(nums.size()==0) return {{}};
    int x = nums.back();//待考虑值
    vector<int> mm = nums;
    mm.pop_back();
    res = fullLine(mm);
    int n = res.size();
    for (int i = 0; i < n;i++){
        auto tmp = res[i];
        res[i].insert(res[i].begin(), x);
        //考察插入
        for (auto it = tmp.end(); it != tmp.begin();it--){
            it = tmp.insert(it, x);
            res.push_back(tmp);
            tmp.erase(it);
        }
    }
    return res;
}

vector<vector<int>> fullLine(const vector<int>& nums){
    vector<vector<int>> res;
    if(nums.size()==0) return {{}};
    int x = nums.back();//待考虑值
    vector<int> mm = nums;
    mm.pop_back();
    auto set = fullLine(mm);
    for (auto& val:set){
        auto tmp =val;
        val.insert(val.begin(), x);
        res.push_back(val);
        //考察插入
        for (auto it = tmp.end(); it != tmp.begin();it--){
            it = tmp.insert(it, x);
            res.push_back(tmp);
            tmp.erase(it);
        }
    }
    return res;
}

前一个靠n来结束循环

后一个res得装所有新的结果

面试题 08.07. 无重复字符串的排列组合

 vector<string> permutation(string S) {
        vector<string> res;
        //S.size()==0
        if(S=="") return {""};//注意是：vector<string>
        char x=S.back();
        S.pop_back();
        res=permutation(S);
        cout<<x<<endl;
        int n=res.size();
        for(int i=0;i<n;i++){
            auto tmp=res[i];
            res[i].insert(res[i].begin(),x);
            for(auto it=tmp.end();it!=tmp.begin();it--){
                it=tmp.insert(it,x);
                res.push_back(tmp);
                tmp.erase(it);
            }
        }
        return res;
    }

char x=S[0]; res=permutation(S.substr(1));

c++字符串和容器使用完全一致

 vector<string> permutation(string S) {
        vector<string> res;
        if(S.size()==0) return {""};//注意是：vector<string>
        char x=S[0];
        auto set=permutation(S.substr(1));
        for(auto& val:set){
            auto tmp=val;
            val.insert(val.begin(),x);
            res.push_back(val);
            for(auto it=tmp.end();it!=tmp.begin();it--){
                it=tmp.insert(it,x);
                res.push_back(tmp);
                tmp.erase(it);
            }
        }
        return res;
    }

回溯

嵌套循环与递归回溯

传入nums数组，请选择其中的n个，输出大小为n的所有排列可能

ex: nums={1,2,3}

则n=2的可能：{1，1}，{1，2}，{1，3}，{2，1}，{2，2}，{2，3}，{3，1}，{3，2}，{3，3}

假设n=3时，则迭代写法为：

vector<vector<int>> fun_loop(const vector<int>& nums){
    vector<vector<int>> res;
    vector<int> tmp;
    int n = nums.size();
    for (int i = 0; i < n;i++){
        tmp.push_back(nums[i]);
        for (int j = 0; j < n;j++){
            tmp.push_back(nums[j]);
            for (int k = 0; k < n;k++){
                tmp.push_back(nums[k]);
                res.push_back(tmp);
                tmp.pop_back();
            }
            tmp.pop_back();
        }
        tmp.pop_back();
    }
    return res;
}

注意：前一层回到上一层需要放弃前一层所选的元素，不然结果会保留上一次的结果

递归写法：

​ 发现迭代写法的特点，每次for的时候都会放入当前下标的值nums[下标]，然后for结束前，也就是内层循环回退到外层循环时，都需要pop也就是放弃已选的元素。这是天然的递归结构

不过在参数传递上，递归时候：递归的函数拷贝当前结果继续使用，所以必须将重要的参数保留

递归函数参数
  • 要么作为全局变量
  • 要么作为函数参数传递，为了保留结果，需要指针或引用方式传递

本题需要递归出口和每次需要加元素存储的vector

------递归出口level,也就是嵌套循环层数

------vector tmp,一个符合要求得到结果

vector<vector<int>> res;
vector<vector<int>> fun_recursion(const vector<int>& nums,vector<int> ans,int level){
    int n = nums.size();
    for (int i = 0; i < n;i++){
        //递归出口
        if(level==3){
            ans.push_back(nums[i]);
            res.push_back(ans);
            ans.pop_back();
        }
        //回溯
        else{
            ans.push_back(nums[i]);
            fun_recursion(nums, ans, level + 1);
            ans.pop_back();
        }
    }
    return res;
}

可以把放元素和放弃元素放在if,else外面

vector<vector<int>> res;//全局变量
vector<vector<int>> fun_recursion(const vector<int>& nums,vector<int> ans,int level){
    int n = nums.size();
    for (int i = 0; i < n;i++){
        //放元素
        ans.push_back(nums[i]);
        //递归出口
        if(level==3){
            res.push_back(ans);
        }
        //回溯
        else{
            fun_recursion(nums, ans, level + 1);
        }
        //放弃当前元素
        ans.pop_back();
    }
    return res;
}

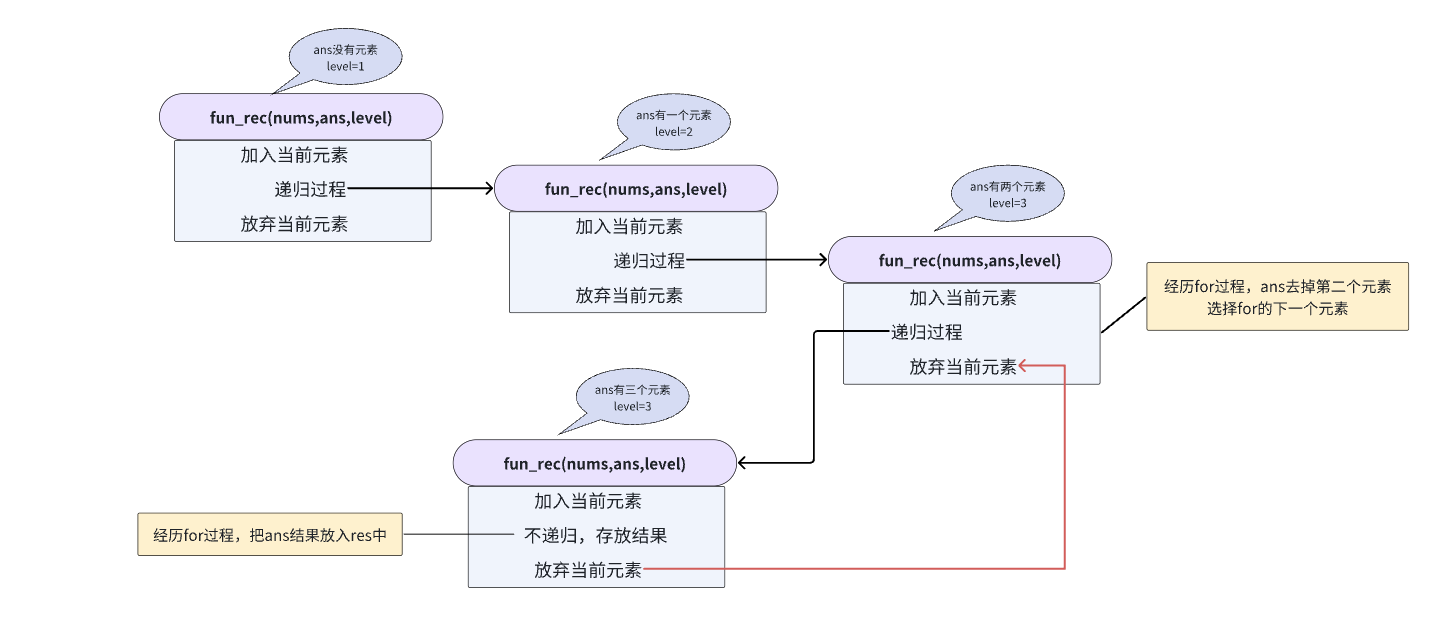
在这里插入图片描述

从结果上来说就是：

在这里插入图片描述

当然也可以把全局变量res作为函数参数，但是需要引用&,因为上一层的结果需要保留

vector<vector<int>> fun_recursion(const vector<int>& nums,vector<int> ans,int level,\
                                  vector<vector<int>>& res){
    int n = nums.size();
    for (int i = 0; i < n;i++){
        //放元素
        ans.push_back(nums[i]);
        //递归出口
        if(level==3){
            res.push_back(ans);
        }
        //回溯
        else{
            fun_recursion(nums, ans, level + 1,res);
        }
        //放弃当前元素
        ans.pop_back();
    }
    return res;
}

主函数：

    vector<int> nums = {11, 22, 33};
    vector<int> mm;
    vector<vector<int>> it;
    auto res=fun_recursion(nums,mm,1,it);

这里递归结束没有return，因为level=3这层for是需要的，也可以把level=4作为递归结束条件，放在程序前。

vector<vector<int>> res;
vector<vector<int>> fun_recursion(const vector<int>& nums,vector<int> ans,int level){
    int n = nums.size();
    //递归出口
        if(level==4){
            res.push_back(ans);
            return res;
        }
    for (int i = 0; i < n;i++){
        //放元素
        ans.push_back(nums[i]);
        //回溯
        fun_recursion(nums, ans, level + 1);
        //放弃当前元素
        ans.pop_back();
    }
    return res;
}

全排列问题

嵌套循环

用迭代写法写出只有三个元素的全排列

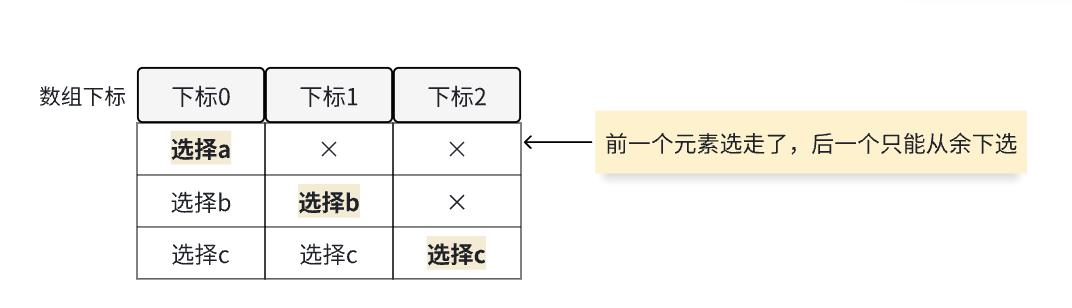
在这里插入图片描述

但是在内层返回外层时候，需要放弃已选择该层元素

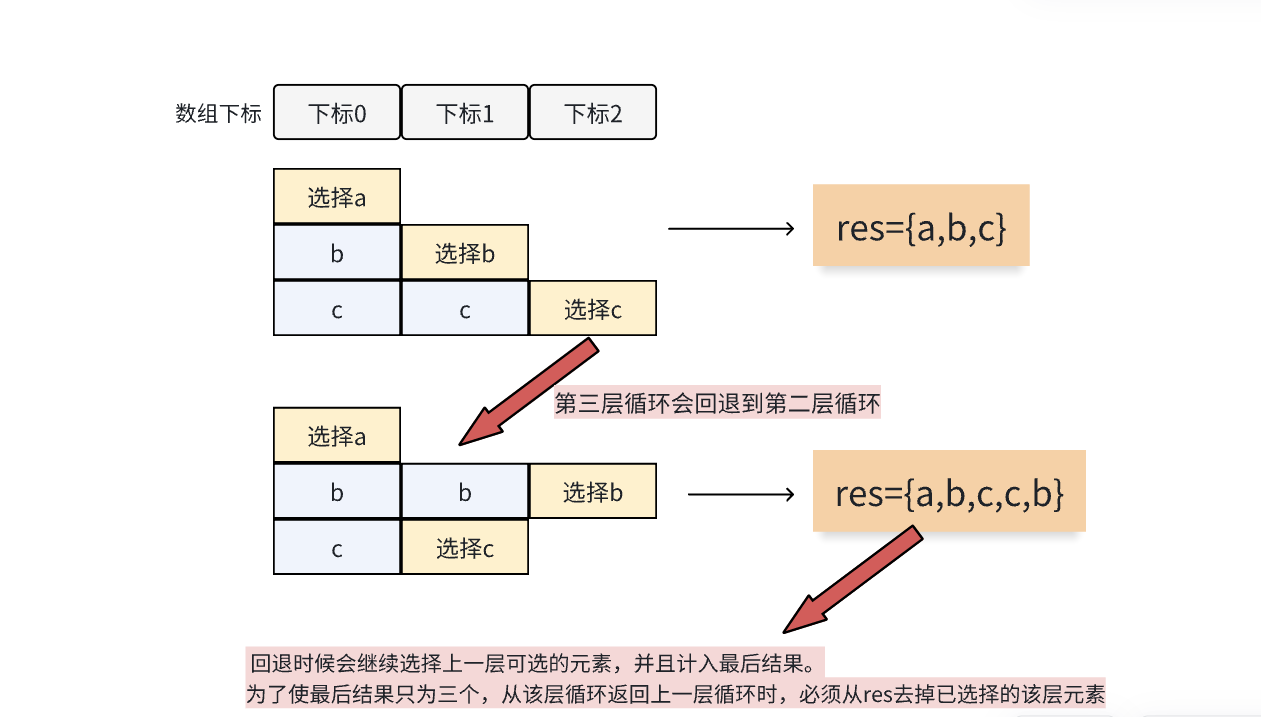
在这里插入图片描述

int main()
{
    vector<int> nums = {11, 22, 33};
    vector<vector<int>> res;
    // 迭代法求3个元素全排列
    // 选1；下一个从2，3中选2；最后只能选3
    for (int i = 0; i < nums.size();i++){
        vector<int> tmp;
        tmp.push_back(nums[i]);
        for (int j = 0; j < nums.size();j++){
            if(j==i)
                continue;
            tmp.push_back(nums[j]);
            for (int k = 0; k < nums.size();k++){
                if(k==i || k==j)
                    continue;
                tmp.push_back(nums[k]);
                //把符合的结果装入res
                res.push_back(tmp);
                //抛去已选的k
                tmp.pop_back();
            }//k
            tmp.pop_back();//回到j前，抛去已选的k
        }//j
    }//i
    traverse(res);
    return 0;
}

迭代法解决全排列问题只能限定元素个数

比如：10个元素10层循环，而且10个for也解决不聊9个元素的循环

静态性：代码仅局限于一个具体问题的求解，而不是一类问题的求解。

递归回溯

循环嵌套自带有回溯能力，内层循环结束会回到它的上一层循环继续执行。

如何放弃重复的元素不选，也就是直接跳过这次结果，方法：设置标记，如果标记后，for不执行本次结果

vector<bool> flag;
vector<vector<int>> res;
vector<vector<int>> fullLine(const vector<int>& nums,vector<int> ans,int level){
    int n = nums.size();
    for (int i = 0; i <n;i++){
        if(!flag[i]){
            //放元素
            ans.push_back(nums[i]);
            flag[i] = true;//该元素已选择
            if(level==3){//不再递归
                res.push_back(ans);
            }
            else{//递归
                fullLine(nums, ans, level + 1);
            }
            //放弃元素
            ans.pop_back();
            //标志置位未选择
            flag[i] = false;
        }
    }
    return res;
}

或者设为全局变量

vector<vector<int>> fullLine(const vector<int>& nums,vector<int> ans,int level,\
                             vector<vector<int>>& res,vector<bool> flag){
    int n = nums.size();
    for (int i = 0; i <n;i++){
        if(!flag[i]){
            //放元素
            ans.push_back(nums[i]);
            flag[i] = true;//该元素已选择
            if(level==3){//不再递归
                res.push_back(ans);
            }
            else{//递归
                fullLine(nums, ans, level + 1,res,flag);
            }
            //放弃元素
            ans.pop_back();
            //标志置位未选择
            flag[i] = false;
        }
    }
    return res;
}

或者：层次大于3时返回结果

vector<vector<int>> res;
vector<bool> flag;
vector<vector<int>> fullLine(const vector<int>& nums,vector<int> ans,int level){
    int n = nums.size();
    if(level>3){//结束递归
        res.push_back(ans);
        return res;
    }
    for (int i = 0; i <n;i++){
        if(!flag[i]){
            ans.push_back(nums[i]); //放元素
            flag[i] = true;//该元素已选择
            fullLine(nums, ans, level + 1);
            ans.pop_back(); //放弃元素
            flag[i] = false; //标志置位未选择
        }
    }
    return res;
}

面试题 08.07. 无重复字符串的排列组合

class Solution {
public:
    vector<string> permutation(string S) {
        vector<bool> _flag(S.size(),false);
        flag=_flag;
        string str;
        getPermute(S,str,1);
        return res;
    }
private:
    vector<string> res;
    vector<bool> flag;
    //str是一次结果，level是记录层数
    void getPermute(string S,string str,int level){
        if(level>S.size()){
           res.push_back(str);
           return;//递归结束
        }
        for(int i=0;i<S.size();i++){
            if(!flag[i]){
                str.push_back(S[i]);
                flag[i]=true;
                getPermute(S,str,level+1);
                str.pop_back();
                flag[i]=false;
            }
        }
    }
};

  • 可以没有level参数，利用str的大小和S的大小

  • 可以把递归放在for内，但是没有return;

class Solution {
public:
    vector<string> permutation(string S) {
        vector<bool> _flag(S.size(),false);
        flag=_flag;
        string str;
        getPermute(S,str);
        return res;
    }
private:
    vector<string> res;
    vector<bool> flag;
    //str是一次结果，level是记录层数
    void getPermute(string S,string str){
        for(int i=0;i<S.size();i++){
            if(!flag[i]){
                str.push_back(S[i]);
                flag[i]=true;
                //装结果
                if(str.size()==S.size()){
                  res.push_back(str);
                }
                //递归
                else{
                getPermute(S,str);
                }
                str.pop_back();
                flag[i]=false;
            }
        }
    }
};

子集问题

迭代写法

下一层循环的开始值要+1，因为一个元素只能被一层选择

vector<vector<int>> subSet(const vector<int>& nums){
    vector<vector<int>> res;
    res.push_back({});//装入空集
    vector<int> ans;
    int n = nums.size();
    for (int i = 0; i < n;i++){
        ans.push_back(nums[i]);
        res.push_back(ans);
        for (int j = i + 1; j < n;j++){//+1
            ans.push_back(nums[j]);
            res.push_back(ans);
            for (int k = j + 1; k < n;k++){//+1
                ans.push_back(nums[k]);
                res.push_back(ans);
                ans.pop_back();
            }
            ans.pop_back();
        }
        ans.pop_back();
    }
    return res;
}
先添加元素再回溯

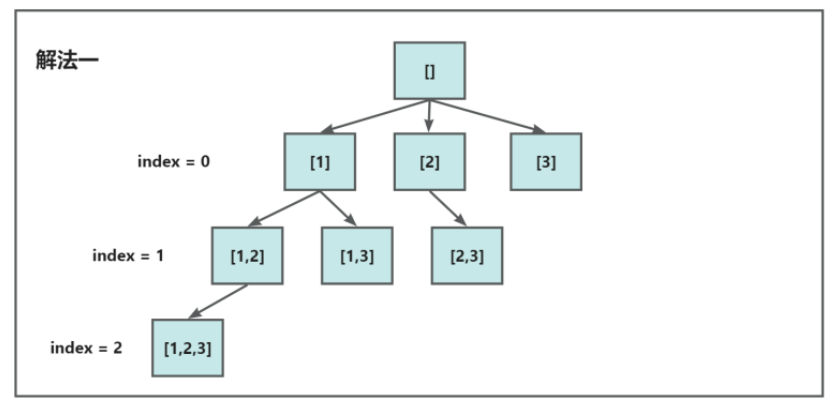
在这里插入图片描述

注意：前一层选择的元素后一层不能选择，所以下一层的初始值是前一层的i值加一

这里由于i值是递归参数，所以自动递归结束，在i==nums.size()时

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<int> mm;
        getSubset(nums,mm,0);//下标从0开始
        return res;
    }
private:
    vector<vector<int>> res;
    void getSubset(vector<int>& nums,vector<int> ans,int index){
        res.push_back(ans);
        int n=nums.size();
        //if(index==n){
        //   return;
        //}
        for(int i=index;i<n;i++){
            ans.push_back(nums[i]);//加入元素
            //回溯
            getSubset(nums,ans,i+1);//i开始值是i+1
            //放弃当前选择
            ans.pop_back();
        }
    }
};

或者把res填入ans放入for内，只是要提前放入空集

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        res.push_back({});//提前加入空集
        vector<int> mm;
        getSubset(nums,mm,0);//下标从0开始
        return res;
    }
private:
    vector<vector<int>> res;
    void getSubset(vector<int>& nums,vector<int> ans,int index){
        int n=nums.size();
        for(int i=index;i<n;i++){
            ans.push_back(nums[i]);
            //res.push_back(ans);
            /*
            if(index==n-1){

            }
            */
            //回溯
            //else
            getSubset(nums,ans,i+1);
            res.push_back(ans);//放在getSubset前后皆可
            //放弃当前选择
            ans.pop_back();
        }
    }
};
先回溯再加元素

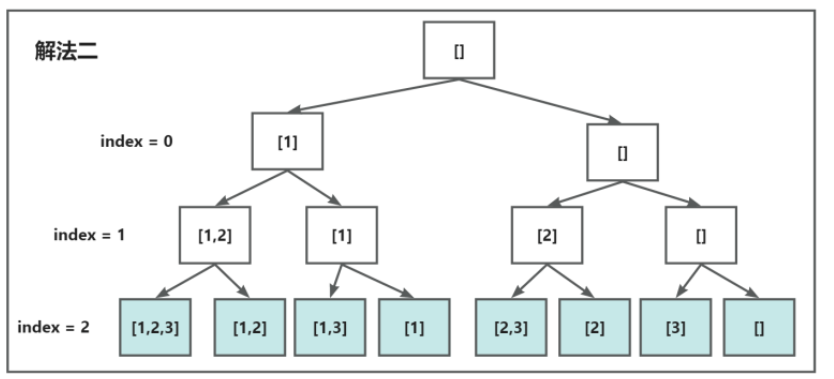
在这里插入图片描述

class Solution {
public:
    vector<vector<int>> subsets(vector<int>& nums) {
        vector<int> mm;
        getSubset(nums,mm,0);
        return res;
    }
private:
    vector<vector<int>> res;
    void getSubset(vector<int>& nums,vector<int> ans,int index){
         if(index==nums.size()){
             res.push_back(ans);
             return;
         }
         //不加入元素
         getSubset(nums,ans,index+1);
         //加入元素
         ans.push_back(nums[index]);
         getSubset(nums,ans,index+1);
         //撤销选择
         ans.pop_back();
    }
};

总结：

这两种解法实质上是相同的，只是在选择添加子集和进行回溯的时机上有所差异。

  • 第一种解法在每次遍历时都会将当前的子集加入到结果集中
  • 而第二种解法则是在递归结束时才将当前的子集加入到结果集中

两个解法的 index 的含义基本一致，作用不同。

  • 它们都表示后续待选择数组的左边界

    • 解法一index是循环的i+1值

    • 解法二会使用 index 作为判断加入结果集的边界条件。

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1472373.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

内衣洗衣机哪个牌子好用？甄选安利四款优质好用的内衣洗衣机

内衣洗衣机哪个牌子好用？甄选安利四款优质好用的内衣洗衣机

内衣洗衣机是近几年新兴的一种家用电器产品&#xff0c;正日益引起人们的重视。但是&#xff0c;面对市面上品牌繁多、款式繁多的内衣洗衣机&#xff0c;使得很多人都不知道该如何选择。身为一个数码家电博主&#xff0c;我知道这类产品在挑选方面有着比较深入的了解。为此&…
阅读更多...
python3GUI--酷狗音乐By:PyQt5（附下载地址）

python3GUI--酷狗音乐By:PyQt5（附下载地址）

文章目录 一&#xff0e;前言二&#xff0e;展示1.主界面2.乐库3.歌单3.频道4.视频5.我的频道6.视频7.听书8.探索9.其他细节1.搜索中间页2.主菜单3.歌单详情4.托盘菜单 三&#xff0e;心得四&#xff0e;总结 一&#xff0e;前言 之前仿作了几款音乐播放器&#xff0c;有的有功…
阅读更多...
【底层解读】ArrayList源码学习

【底层解读】ArrayList源码学习

成员变量 学习源码前&#xff0c;我们还是先看一下ArrayList中成员变量有哪些 构造函数 ArrayList一共有三个构造函数。 第一个&#xff1a;带有指定初始容量的构造函数 第二个&#xff1a;空参构造 第三个&#xff1a;包含指定集合的构造函数 OK&#xff0c;看完构造函数&a…
阅读更多...
Numpy 数组添加行

Numpy 数组添加行

参考&#xff1a;Add Row to Numpy Array 在机器学习和数据分析中&#xff0c;经常需要处理大型数据集。Numpy是Python中一个非常有用的库&#xff0c;它提供了高性能的多维数组对象以及用于处理这些数组的函数。在Numpy中&#xff0c;可以使用numpy.append()函数来添加行到一…
阅读更多...
【Git教程】（三）提交详解 —— add、commit、status、stach命令的说明，提交散列值与历史，多次提交及忽略 ~

【Git教程】（三）提交详解 —— add、commit、status、stach命令的说明，提交散列值与历史，多次提交及忽略 ~

Git教程 提交详解 1️⃣ 访问权限与时间戳2️⃣ add命令与 commit 命令3️⃣ 提交散列值4️⃣ 提交历史5️⃣ 一种特别的提交查看方法6️⃣ 同一项目的多部不同历史6.1 部分输出&#xff1a;-n6.2 格式化输出&#xff1a;--format、--oneline6.3 统计修改信息&#xff1a;--st…
阅读更多...
异常的处理

异常的处理

文章目录 1. 异常概述1.1 异常总结&#xff1a;1.2 什么是程序的异常1.3 异常的抛出机制1.4 如何对待异常 2. Java异常体系2.1 Error和Exception2.2 Throwable2.3 编译时异常和运行时异常 3. 常见的错误和异常3.1 Error3.2 运行时异常3.3 编译时异常 4. 异常的处理4.1 异常处理…
阅读更多...
大好河山集团带医生的旅游团 守护旅客安康多年

大好河山集团带医生的旅游团 守护旅客安康多年

回首大好河山集团成立之初&#xff0c;大好河山就秉持着对旅客安康的关切&#xff0c;怎么能让较高年龄的老人也能畅游祖国的大好河山&#xff0c;是大好河山集团迫切需要解决的问题&#xff0c;因此大好河山集团旗下部分旅游团设有带医生的旅游团为此类游客服务&#xff0c;他…
阅读更多...
docker容器技术（2）

docker容器技术（2）

docker容器数据卷 什么是数据卷&#xff1f; 在Docker中&#xff0c;数据卷&#xff08;Data Volumes&#xff09;是一种特殊的目录&#xff0c;可以在容器和主机之间共享数据。它允许容器内的文件持久存在&#xff0c;并且可以被多个容器共享和访问。 数据卷的主要作用如下&am…
阅读更多...
Pycharm 配置Django 框架

Pycharm 配置Django 框架

Pycharm 配置Django 框架 一、创建第一个django项目 先在自己所在盘创建一个文件夹”projectDjango“ 二、打开pycharm专业版&#xff0c;打开刚刚新建的“projectDjango”项目。 三、打开菜单栏“File"->“Settings” 选择自己安装的python版本 四、安装Django库 1.点…
阅读更多...
浅浅的画一个STDP的图像吧

浅浅的画一个STDP的图像吧

stdp最重要的是两个窗口函数 根据这个方程我们刻画出他的轨迹&#xff0c;代码如下 import numpy as np import matplotlib.pyplot as plt# 定义STDP参数 tau_pos 30 # 正向突触权重变化的时间常数 tau_neg 30 # 负向突触权重变化的时间常数 A_pos 0.1 # 正向突触权重变…
阅读更多...
解决谷歌浏览器，每次重启都重置所有设置的问题

解决谷歌浏览器，每次重启都重置所有设置的问题

一、问题&#xff1a; 修改谷歌浏览器的设置 关闭浏览器再打开设置页面后&#xff0c;会显示&#xff08;部分设置已重置Chrome检测到您的部分设置被其他程序篡改了&#xff0c;因此已将这些设置重置为原始默认设置。了解详情&#xff09; 之前的设置被重置了 二、解决 创建—…
阅读更多...
Python入门必学：print函数--从基础语法到高级用法

Python入门必学：print函数--从基础语法到高级用法

Python入门必学&#xff1a;print函数–从基础语法到高级用法 &#x1f308; 个人主页&#xff1a;高斯小哥 &#x1f525; 高质量专栏&#xff1a;Matplotlib之旅&#xff1a;零基础精通数据可视化、Python基础【高质量合集】、PyTorch零基础入门教程 &#x1f448; 希望得到您…
阅读更多...
1.0 RK3399项目开发实录-Ubuntu环境搭建（物联技术666）

1.0 RK3399项目开发实录-Ubuntu环境搭建（物联技术666）

1.下载Ubuntu所需的版本&#xff1a;Index of /releases 2.安装vmplayer:Download VMware Workstation Player | VMware 3.安装Ubuntu时&#xff0c;磁盘空间尽量大些&#xff0c;开发板系统包都比较大&#xff0c;避免存不下&#xff0c;建议空间100G。 关闭Ubuntu自动更新…
阅读更多...
MYSQL--(1.存储引擎 *2.事务*)

MYSQL--(1.存储引擎 *2.事务*)

一 存储引擎: 1.介绍 1>在数据库管理系统当中通过使用数据引擎来实现数据的增删改,查询 2>不同的存储引擎提供的有不同的存储机制,索引技巧等功能 MYSQL的核心,就是存储引擎 3>同样的,用户也可以根据自己的需要进行选择,更改自己需要…
阅读更多...
机器学习YOLO操作全流程​​编

机器学习YOLO操作全流程​​编

YOLO介绍 Ultralytics YOLOv8，是最新的著名实时目标检测和图像分割模型。它基于深度学习和计算机视觉的最新进展，提供了无与伦比的速度和精度性能。由于其精简的设计，适用于各种应用，并且可以轻松适配不同的硬件平台，从边缘设备到云端API。 探索 YOLOv8 文档，这是一个全…
阅读更多...
Unity类银河恶魔城学习记录7-9 P75 Saw spin sword源代码

Unity类银河恶魔城学习记录7-9 P75 Saw spin sword源代码

Alex教程每一P的教程原代码加上我自己的理解初步理解写的注释&#xff0c;可供学习Alex教程的人参考 此代码仅为较上一P有所改变的代码 【Unity教程】从0编程制作类银河恶魔城游戏_哔哩哔哩_bilibili Sword_Skill_Controller.cs using System.Collections; using System.Col…
阅读更多...
数据可视化--了解数据可视化和Excel数据可视化

数据可视化--了解数据可视化和Excel数据可视化

目录 1.1科学可视化&#xff1a; 可视化是模式、关系、异常 1.2三基色原理&#xff1a; 三基色:红色、绿色和蓝色 1.3Excel数据可视化 1.3.1 excel数据分析-13个图表可视化技巧 1.3.2 excel数据分析-28个常用可视化图表&#xff08;video&#xff09; 1.3.3Excel可视化…
阅读更多...
DM数据库学习之路(十六）DEM部署DM8DPC集群

DM数据库学习之路(十六）DEM部署DM8DPC集群

DEM部署DPC集群 DPC准备工作 在所有安装DPC服务器上部署dmagent&#xff0c;dmagent的运行环境需要依赖JAVA环境&#xff0c;JAVA版本必须为JAVA1.8。 创建用户 所有安装DPC服务器&#xff0c;手工建dmdba用户 # groupadd dinstall # useradd -g dinstall -d /home/dmdba…
阅读更多...
PHP中的飞碟运算符、取反运算符、对比非ASCII字符串、对比浮点数操作

PHP中的飞碟运算符、取反运算符、对比非ASCII字符串、对比浮点数操作

对比浮点数 在电脑里存储的浮点数可能会和输入的值有些许差异&#xff0c;比如输入的是10.0&#xff0c;但存储的是10.00001. 在比较两个浮点数是否相等时可以计算下两个数的差值&#xff0c;然后查看下两数之差是否小于可以接受的阈值&#xff0c;如果要求精度在小数点后5位的…
阅读更多...
【Spring Boot 源码学习】深入 BootstrapContext 及其默认实现

【Spring Boot 源码学习】深入 BootstrapContext 及其默认实现

《Spring Boot 源码学习系列》 深入 BootstrapContext 及其默认实现 一、引言二、往期内容三、主要内容3.1 BootstrapContext3.1.1 源码初识3.1.2 get 方法3.1.3 getOrElse 方法3.1.4 getOrElseSupply 方法3.1.5 getOrElseThrow 方法3.1.6 isRegistered 方法 3.2 ConfigurableB…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023