---

一、Q learning

value-based的方法，评论家不会直接决定行动。给定一个演员π，它评价这个演员有多优秀。状态值函数Vπ(s)：当使用行动者π时，累积奖励期望在访问状态s后获得（预测）。

critic是绑定了某个actor预测这个actor的分数。

评估状态值函数Vπ(s)

MC

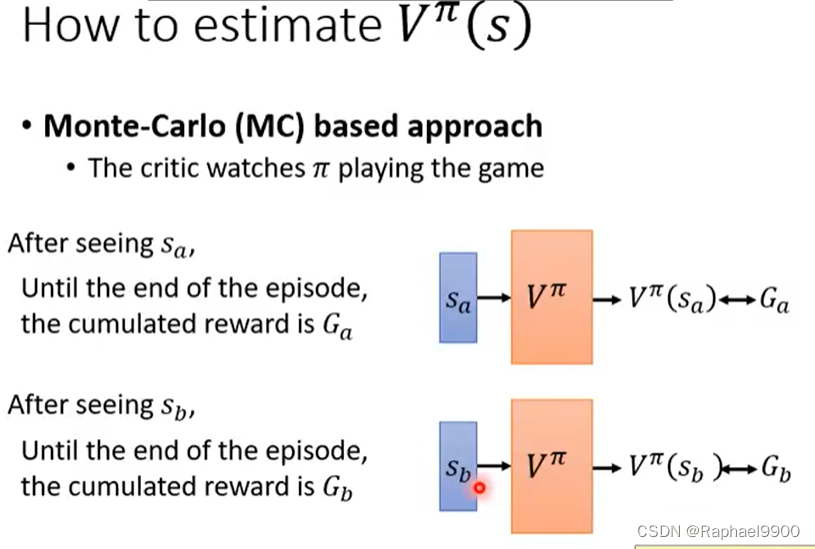
要把游戏玩到结束，才能更新网络参数，得出分数。

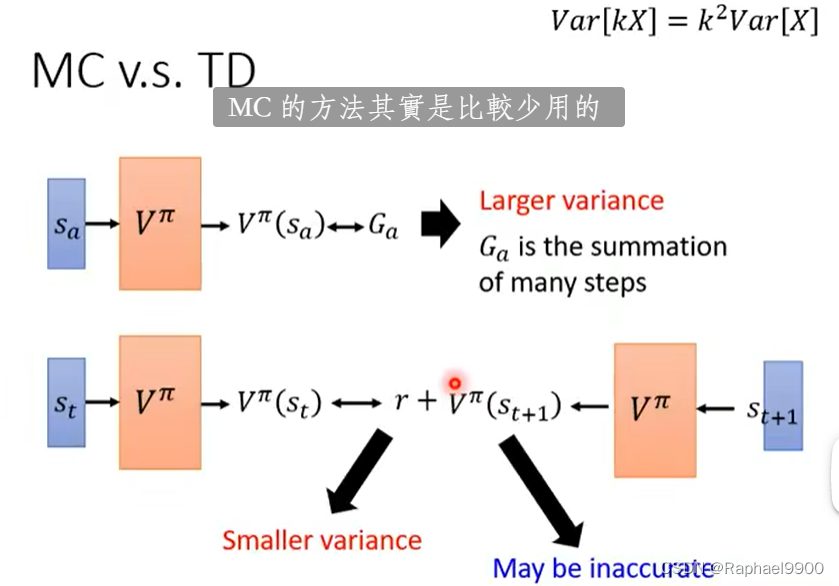
TD

MC的随机性大，所以有很大的方差；而TD方法不一定是准确的。


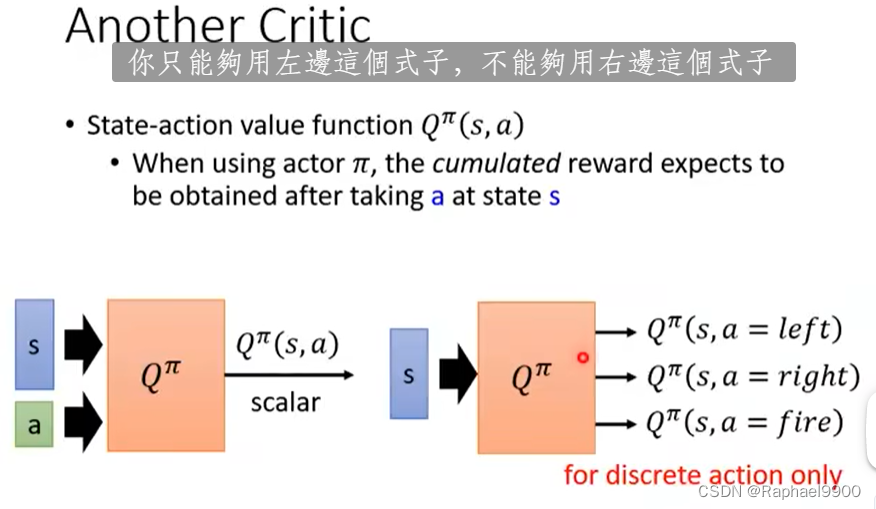
状态-动作值函数Qπ(s，a)，当使用行动者π时，期望在状态s采取a后获得累积奖励。
action是无法穷举的就要左边的，右边的式子仅用于离散动作



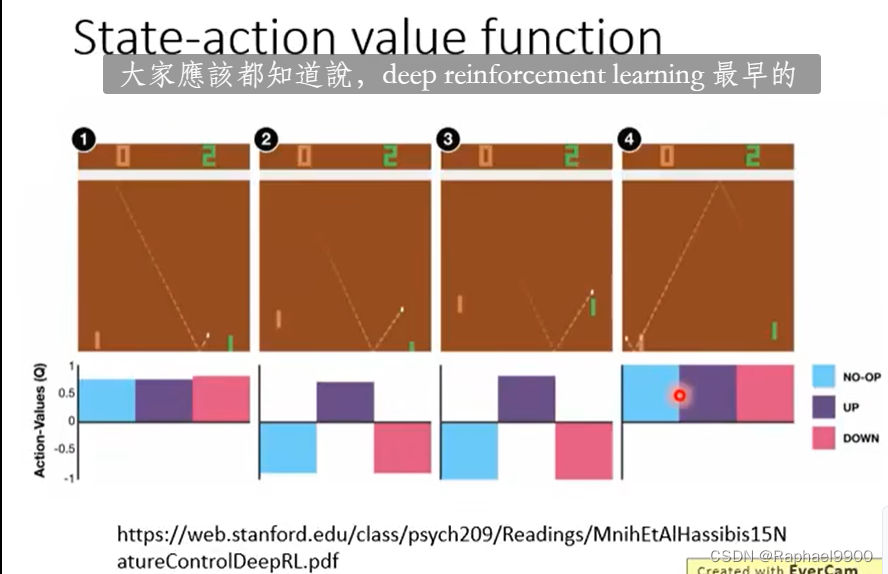
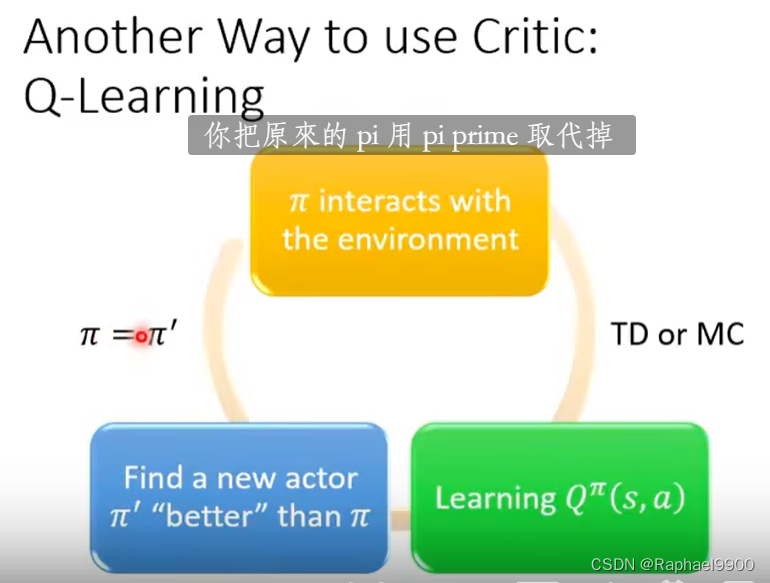
一直循环之后就会得到好的方程。
给出所有action，找到会让Q最大的动作，就是π’。但是这个不适合a是连续的情况（a是离散的适合）


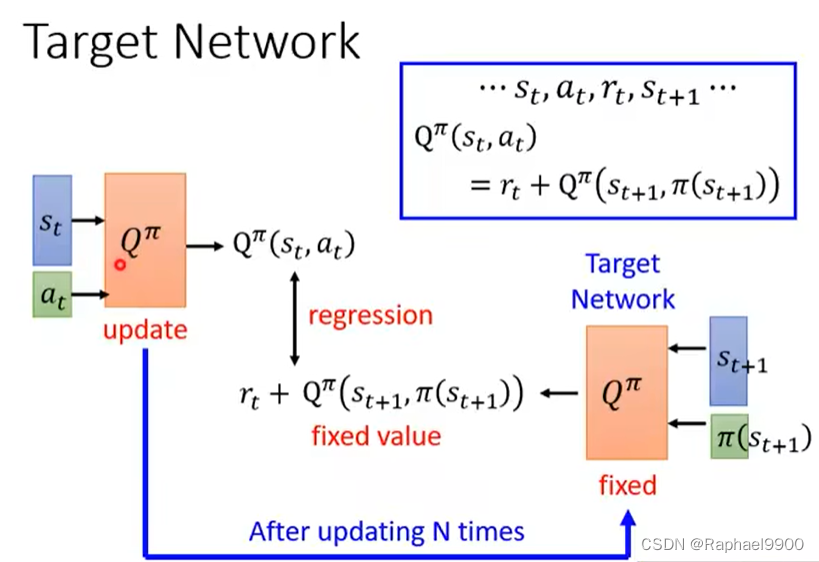
实际上Q’是会变的，那我们的目标就会一直在变（让Q接近Q’），所以我们要固定住一个Q’，更新另一个Q。更新了很多次Q，我们就更新一次Q‘。

如果是没有看过的动作，那可能都会是初始化的估值，而只要看过一个，那就是1的Q，其他都是0，就不会试试其他的动作。

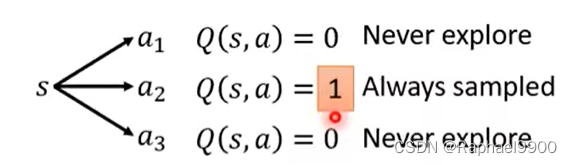
epsilon greedy：E在刚开始训练的时候值比较大，后面就会变小。E一般是很小的值，有很大概率用来估测Q，而小概率是用随机性。在action 空间里面加noisy。
Boltzmann Exploration：对Q取对数然后做常规化（除Q的对数的和）。在刚开始Q的输出分布可能是很一致的。

把所有收集的资料都放到replay buffer里面（可能有以前训练的不同的policy计算的数据，满了才会丢掉），存的是s，a，r，s。

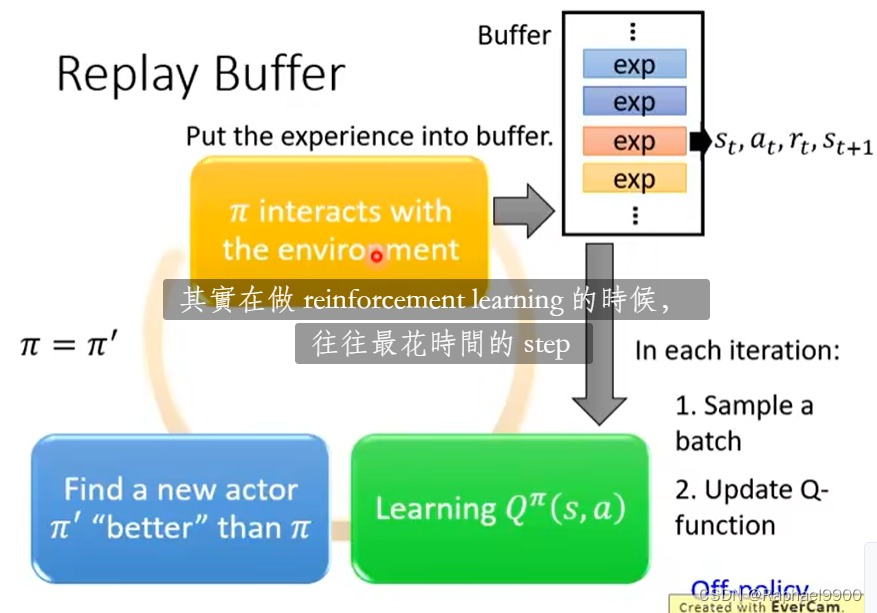
好处：同一个batch有多种多样的资料，这样会避免让网络坏掉。虽然有过去的资料，但是这样是没问题的。这样类似于off-policy的做法，不会那么花时间去收集资料。

上面的错误：是从buffer里面取batch。

double DQN

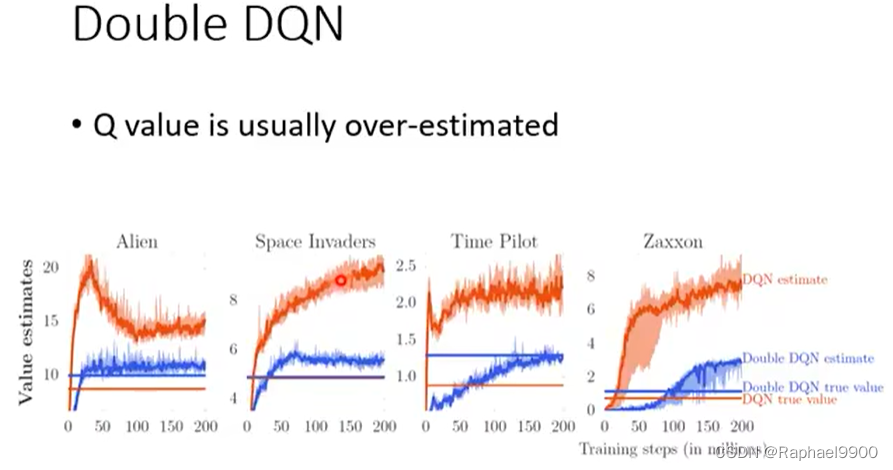
DQN总是高估（穷举所有的a让Q最大的那个a）

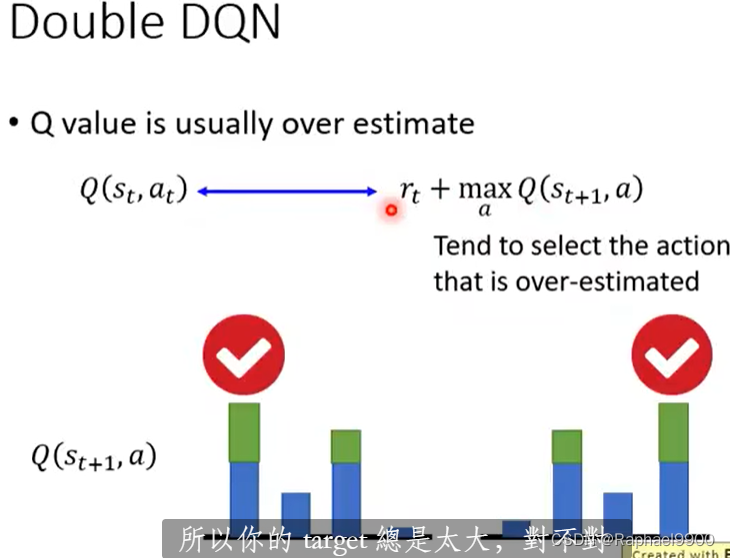
double DQN选择a的那个Q和计算Q不一样。如果Q高估了a，那么它被选中。Q’会给它适当的值。
Q '高估怎么样？Q不会选择该动作。

用能更新参数的Q去选择a，用固定参数的Q’去计算value。

dueling DQN

唯一的改变：改变网络的结构。

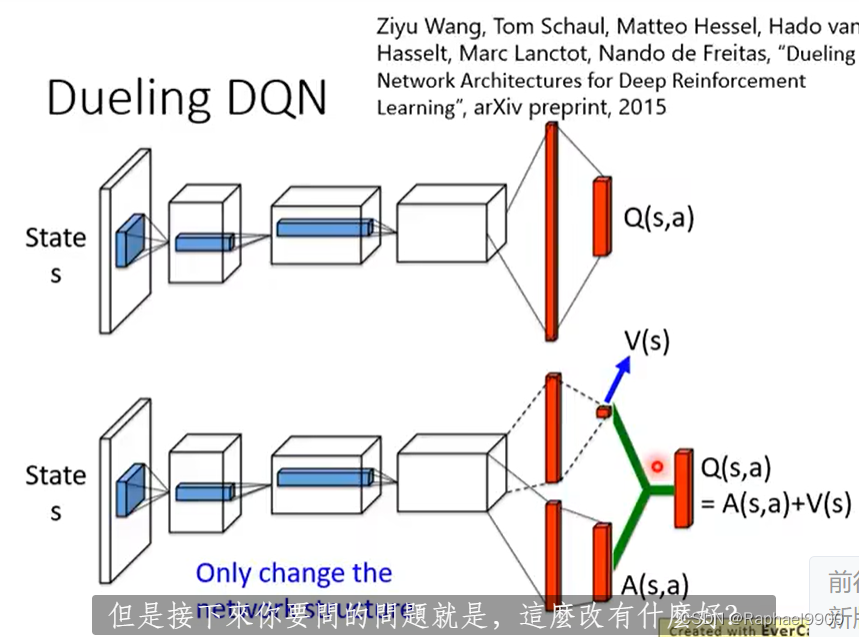
更新V之后，就会更新Q，这样就会有效率

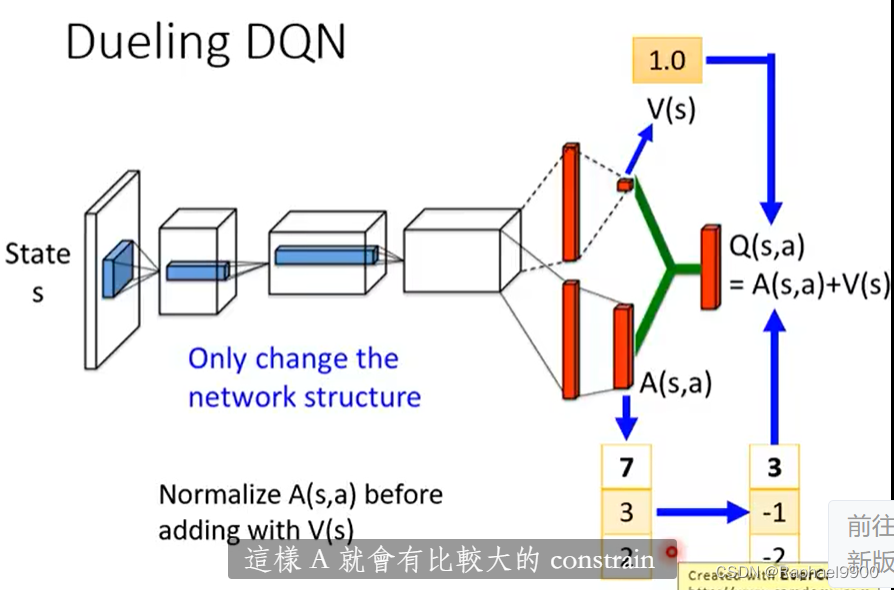
prioritized reply

对于buffer里面的数据，如果有些数据是比较重要的，而有些数据是训练不好的，那就不能一致取样。先前训练中TD误差较大的数据被采样的概率较高。

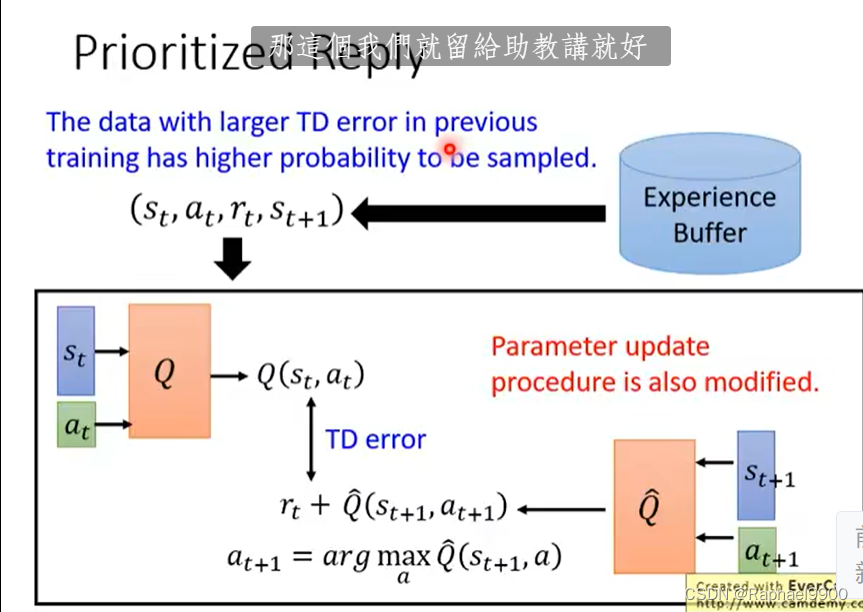
不止改变取样数据的分布，也改变训练的过程。

multi-step

MC和TD之间的平衡

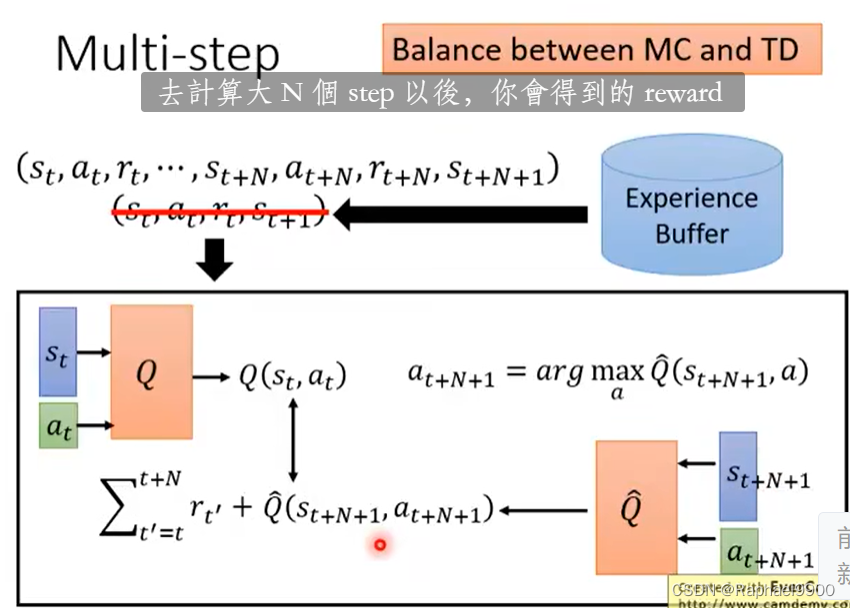
结合两个方法，取样了多个step之后才估测value，估测的部分的影响就会比较轻微。因为加入了N项r，所以variance就会比较大，可以调整N，让它平衡。

noisy net

在参数的空间上加noisy。在Q网络的 参数上面加噪声得到Q~。
把每个参数都加上噪声。在每集开始之前将噪声注入Q函数的参数中（得到action之前），得到的这个就是Q~就是固定住参数的，用来训练的。
在同一个episode里面，Q~的参数是固定的，只有下一个episode才更新参数，重新取样噪声。

动作噪音noise on action：给定相同的状态，代理agent可能采取不同的动作（epsilon greedy，因为是在action里面加上噪声，随机性大）。没有真正的策略是这样运作的（希望同样的状态得到一样的动作）。
参数噪声noise on parameters：给定相同(相似)的状态，代理采取相同的动作。→依赖于状态的探索exploration，以一致的方式探索。在一个episode里面，网络的参数是一致的，所以同一个状态会输出一样的东西。

distributional

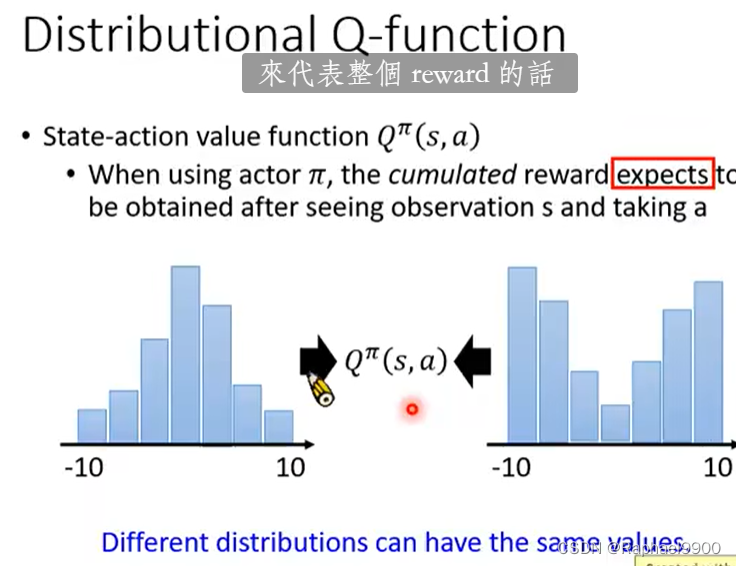
状态-动作值函数Qπ(s，a)：当使用行动者π时，期望在看到观察值s并采取a后获得累积奖励。
不同的分布可以有同样的期望expectation。这时候就会有些loss，有些信息是没有用到的。

每个动作有5个框,可以选择同样期望，但是风险更小的动作。（这种方法可以输出概率分布，同一个动作的分布总和是1）

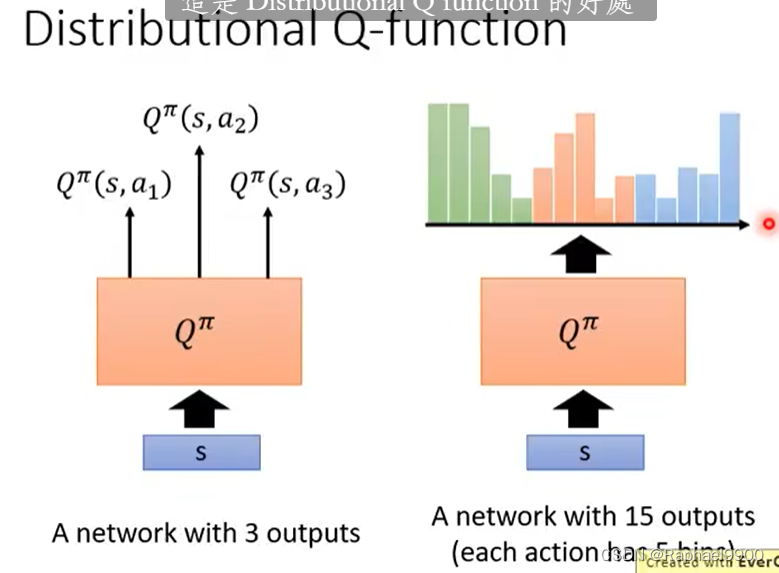
这里可能会有低估reward的情况，会把极端的值丢掉。

rainbow

混合所有的方法

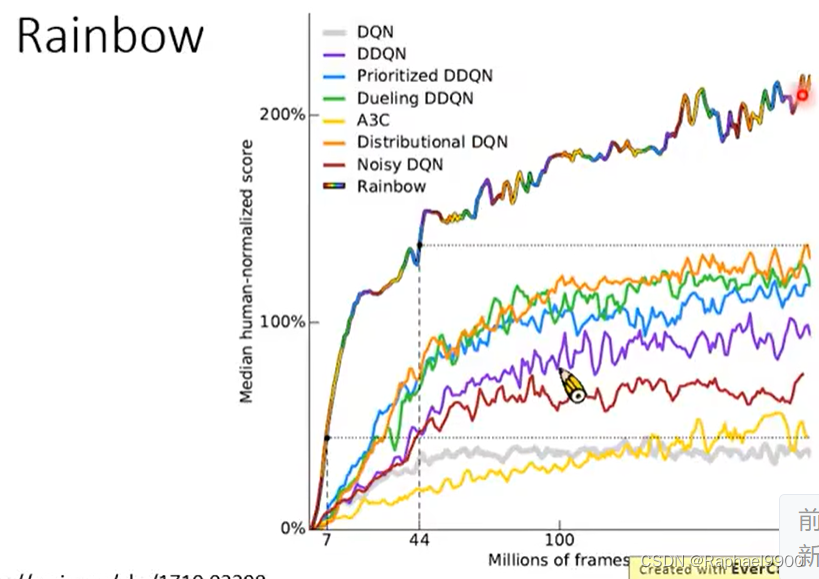
去掉某一种方法之后：

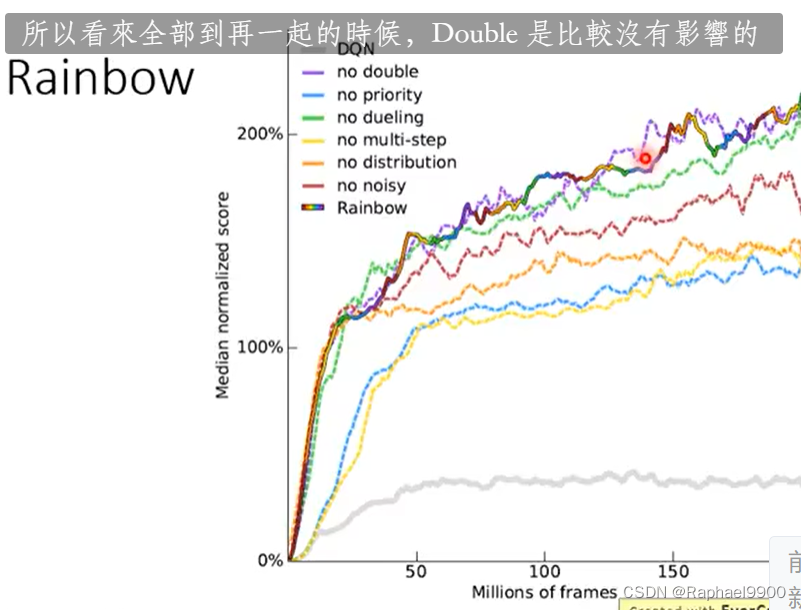
避免高估奖励才加了双DQN

二、Q-learning for continuous actions

estimate Q方程比较容易，只要得到Q方程，就能得到好的策略。问题：不容易处理连续的动作。
在之前，动作是离散的，就能穷举所有的a，算出最好的a。
方法1：取样得到N个a，找到最大的a。但是不能取样所有的a，所以可能不准确。
方法2：使用梯度上升的方法解决最优化问题。问题：全局最大问题，运算量也很大，还要循环更新参数。
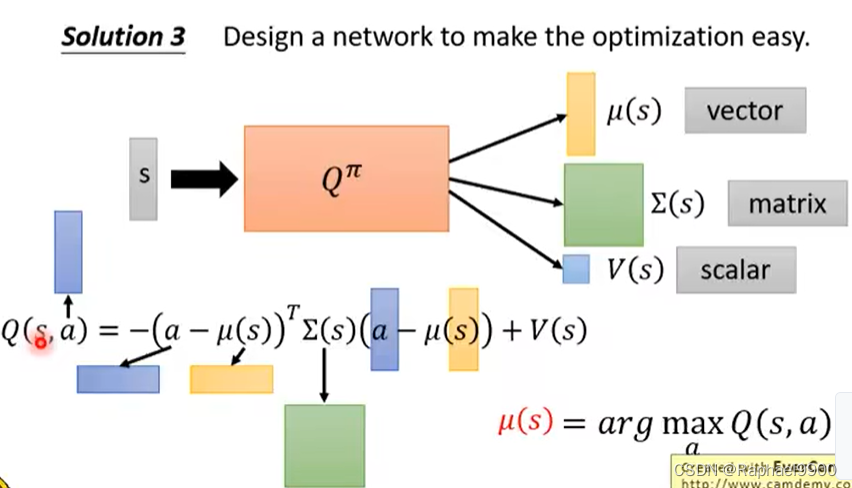
方法3：特别设计Q网络去让最优化容易。Q方程是输入s和a，输出V。先输入s，得到三东西（向量，矩阵，数值），然后输入a，让a和μ相减，a此时是连续的向量，然后做其他的运算。这里我们需要让Q最大，也就是第一项最小，那就能让最大的a=μ（s）.在这里μ是高斯均值，Σ（s）是正定的variance（在Qπ里面不是直接输出这个矩阵，而是跟一个矩阵做transpose相乘，保证是正定的）。

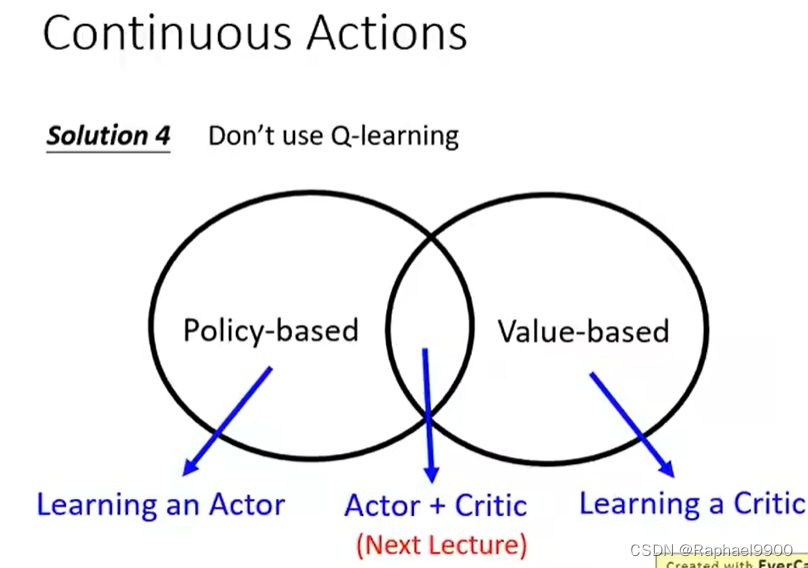
三、关于深度学习的猜想

几乎所有的局部最小值都具有与全局最优值非常相似的损失，因此找到一个局部最小值就足够了。
当我们遇到一个临界点时，它可能是鞍点或局部最小值。

有个正和一个负的就是saddle point

当E比较小的时候，特征值很可能是正的，那就可能遇到局部最小值。saddle point比较容易出现在loss高的地方，局部最小值容易出现在loss低的地方。



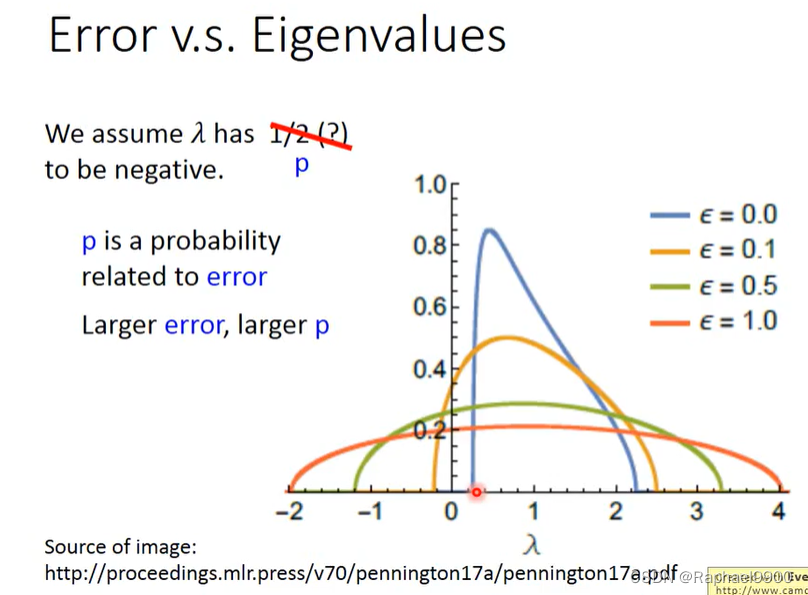
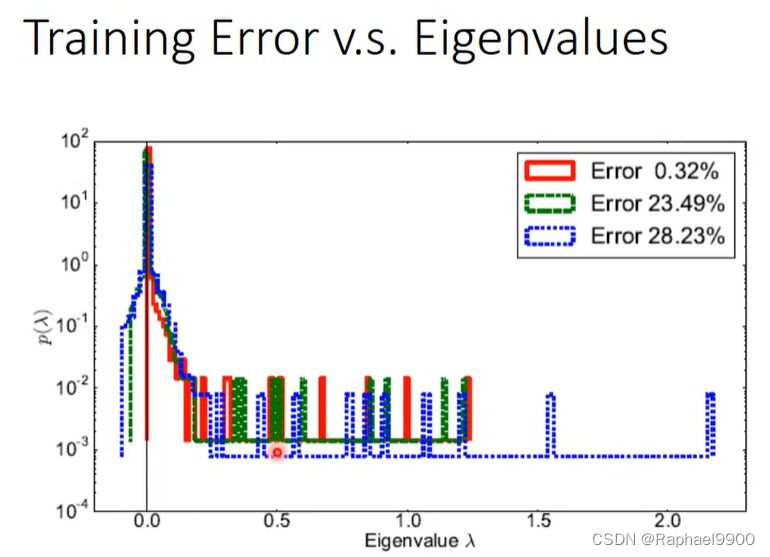
当critical point越像局部最小值，training error就越接近0.


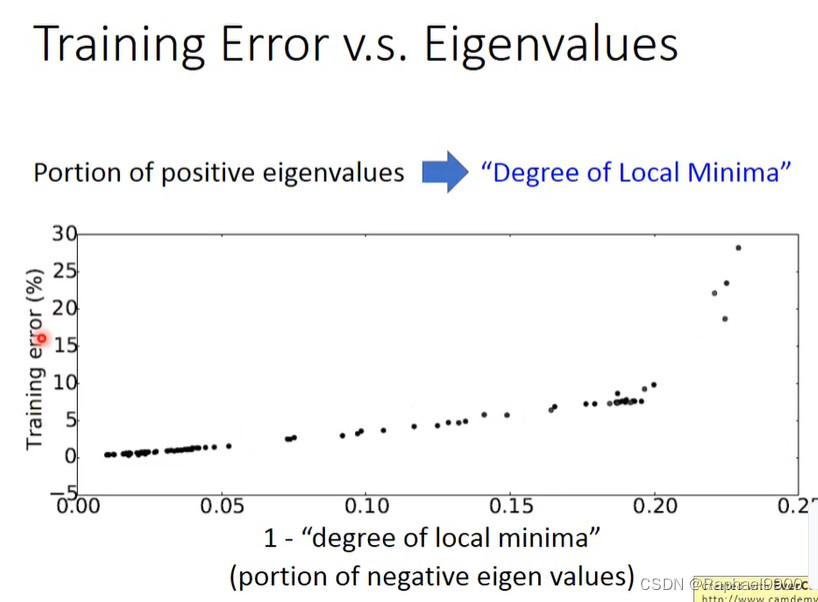
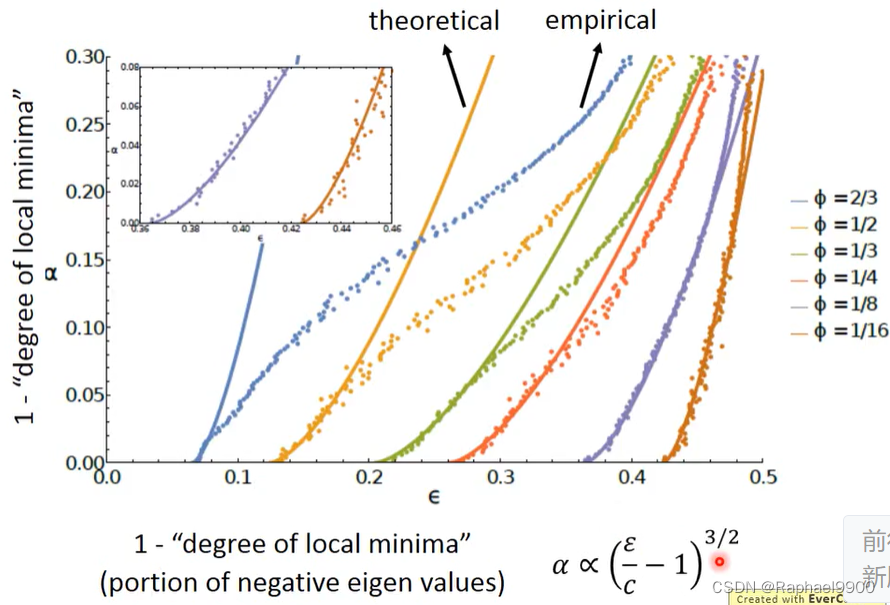
深度学习与具有7个假设的spin glass模型相同。

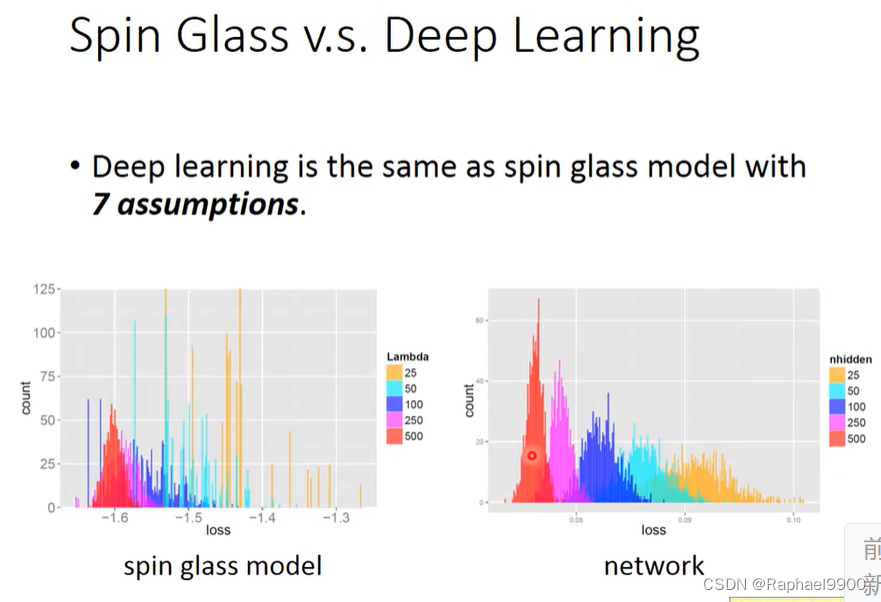
模型越大，loss越接近一个较低的值。
如果网络的规模足够大，我们可以通过梯度下降找到全局最优解，独立于初始化。