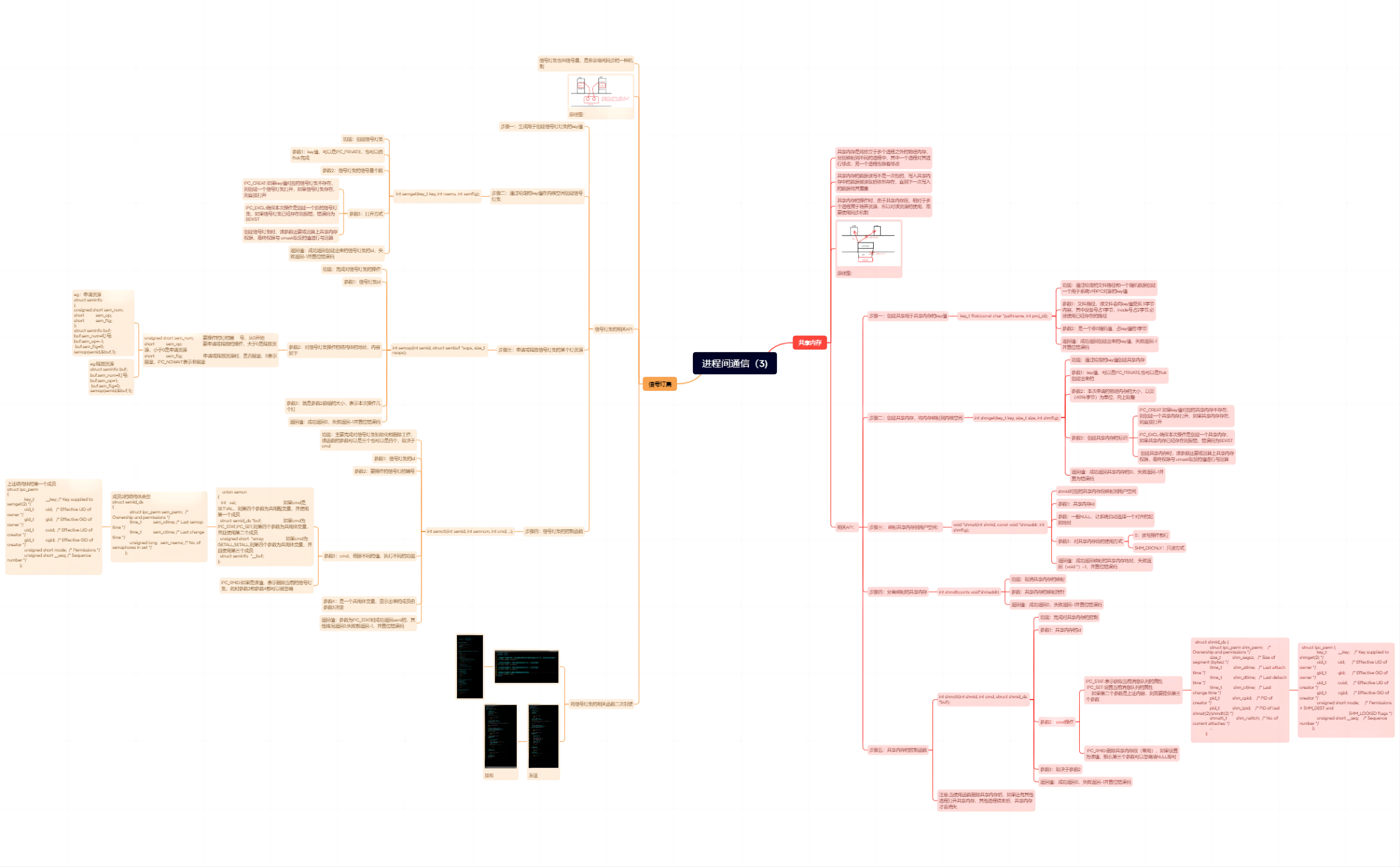
Title: GTSAM 中的鲁棒噪声模型与 M-估计 (GTSAM Robust Noise Model and M-Estimator)

---

---

前言

查看 GTSAM 文档^[1] (/gtsam/doc/robust.pdf) 过程中做了一些推导, 记录一下.

主要围绕对因子图优化计算中对离群点的抑制而展开.

---

I. 噪声模型

借用 gtsam4.2 中文档 /doc/html/a04892.html 对噪声模型因子的描述.

gtsam::NoiseModelFactor Class Reference

A nonlinear sum-of-squares factor with a zero-mean noise model implementing the density
$$P(z|x)\propto \exp (-0.5|z-h(x){|}_C^2)$$
Templated on the parameter type X and the values structure Values.

There is no return type specified for h(x). Instead, we require the derived class implements
$$error\_vector(x)=h(x)-z\approx A\delta x-b$$
This allows a graph to have factors with measurements of mixed type.

The noise model is typically Gaussian, but robust and constrained error models are also supported.

由之前的博文 “因子图、边缘化与消元算法的抽丝剥茧” 中的定义, 构建因子图
$$\Phi (\Theta )=\prod _i{\varphi }_i({\Theta }_i)\text{\hspace{1em}(I-1)}$$
其中 $\Theta \triangleq (X,L)$, ${\Theta }_i\triangleq \mathcal{N}({\varphi }_i)$, ${\Theta }_i$ 即为与因子 ${\varphi }_i$ 有关的变量 (包括机器人状态变量与路标变量).

如果每个因子都具有高斯噪声/高斯分布,
$${\varphi }_i({\Theta }_i)\propto \exp \left(-\frac{1}{2}\Vert h_i({\Theta }_i)-z_i{\Vert }_{{\Sigma }_i}^2\right)\text{\hspace{1em}(I-2)}$$
其中 $h_i(\cdot )$ 和 $z_i$ 分别为测量函数和测量值, ${\sum }_i$ 为测量值 $z_i$ 的误差协方差矩阵.

那么, 可以对因子图求最大后验估计 (MAP, Maximum a Posteriori),
$${\Theta }^{\ast }=\underset{\Theta }{\mathrm{argmax}}\Phi (\Theta )=\underset{\Theta }{\mathrm{argmax}}\left(\prod _i{\varphi }_i({\Theta }_i)\right)\text{\hspace{1em}(I-3)}$$
如果对式 (I-1) 两边先求 $-\log$ 运算再求极小值可得^{[2], [3]}
$${\Theta }^{\ast }=\underset{\Theta }{\mathrm{argmin}}\left[-\log \Phi (\Theta )\right]=\underset{\Theta }{\mathrm{argmin}}\frac{1}{2}\sum _i\Vert h_i({\Theta }_i)-z_i{\Vert }_{{\Sigma }_i}^2\text{\hspace{1em}(I-4)}$$
这样就将高斯噪声模型描述下的因子图的最大后验推理等价转换为非线性最小二乘问题.

噪声模型在整个因子图中的作用可由式 (I-2) 体现. 由 gtsam::NoiseModelFactor Class Reference 可知, 除了上述我们最熟悉的高斯噪声模型以外, 也支持鲁棒噪声模型 —— 本文的主角.

---

II. 鲁棒回归 —— M 估计

因为我们所谓的 “二乘” 是误差的平方, 一旦出现一个误差值远远偏离于正常误差, 在经过平方后, 该粗差对目标函数的影响巨大. 即存在离群值 (Outlier) 时,

最小二乘估计获得的结果可能远离真值, 则估计结果不可靠/不可信, 是离群值污染了正常的数据.

针对最小二乘法的这个问题, 逐渐发展出鲁棒回归 (Robust Regression), 其中最通用的方法是 M 估计 (M-Estimation)^[4]. M 估计是基于最小二乘估计发展起来的一种抗差估计 (Robust Estimation) 方法.

本章节对 M 估计进行介绍^[4]并简单推导, 再在下一章节中应用于因子图.

---

1. 线性回归

假设对如下线性模型进行 $n$ 观测:
$$y_i={\beta }_0+{\beta }_1{x}_{i1}+{\beta }_2{x}_{i2}+\cdots +{\beta }_k{x}_{ik}+{\epsilon }_i(i=1,2,\cdots ,n)\text{\hspace{1em}(II-1-1)}$$
定义 $\mathbf{b}\triangleq {\left[\begin{array}{ccccc}{\beta }_0& {\beta }_1& {\beta }_2& \cdots & {\beta }_k\end{array}\right]}^{\mathrm{T}}$ 为待估计参数 (或待估计变量), ${\mathbf{x}}_i^{{}^{\prime }}\triangleq \left[\begin{array}{ccccc}1& x_{i1}& x_{i2}& \cdots & x_{ik}\end{array}\right]$ 为扩展的数据向量. 则上式可以简写为
$$y_i={\mathbf{x}}_i^{{}^{\prime }}\mathbf{b}+{\epsilon }_i\text{\hspace{1em}(II-1-2)}$$
对应的预测值为
$${\hat{y}}_i={\mathbf{x}}_i^{{}^{\prime }}\mathbf{b}\text{\hspace{1em}(II-1-3)}$$
残差/误差为
$$e_i=y_i-{\hat{y}}_i=y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b}\text{\hspace{1em}(II-1-4)}$$

---

2. 损失函数

在回归模型式 (II-1-1)下, 用来量化估计模型的预测值与真实值的不一致程度 (量化回归效率) 的工具称为损失函数, 记为 $\rho (e_i)$.

最常用的损失函数是均方误差 (Mean Square Error, MSE), 也称为 L2 损失, 即
$${\rho }_{L_2}(e_i)=e_i^2\text{\hspace{1em}(II-2-1)}$$
L2 损失就是最小二乘法对应的损失函数. 根据本节前部的分析, L2 损失对离群值不鲁棒. 同时, 其最优特性依赖于高斯假设, 当遇见非高斯噪声时, 估计结果也变得不可靠^[5].

第二种常用的损失函数为平局绝对误差 (Mean Absolute Error, MAE), 也称为 L1 损失, 即
$${\rho }_{L_1}(e_i)=|e_i|\text{\hspace{1em}(II-2-2)}$$
因为 L1 面对离群点时误差不再是平方放大, 鲁棒性有了提高.

但 L1 在中心点不可导, 是缺陷之一.

另外, 在梯度下降算法中, MSE 能够快速准确地收敛, 而 MAE 收敛速度较慢.

也就是 MSE 和 MAE 各有优缺点, 那么自然希望能够构建取长补短的损失函数.

第三种常用的损失函数是 Huber 损失函数 (Huber Loss), 也称为平滑 L1 损失. 表达式为
$${\rho }_H(e)=\{\begin{array}{clc}\frac{1}{2}{e}^2,& & \text{for}|e|\le k\\ k|e|-\frac{1}{2}{k}^2,& & \text{for}|e|>k\end{array}\text{\hspace{1em}(II-2-3)}$$
其中 $k$ 是一个非负参数, 用来控制损失函数的二次区域与线性区域的范围. 当残差大于 $k$ 时采用 L1 损失, 残差小于等于 $k$ 时采用 L2 损失.

Huber 损失函数结合了 L1 损失和 L2 损失的优点, 比起 L2 损失来它对离群值更鲁棒, 同时在中心点处可导^[5].

当采用梯度下降类算法时, 迭代值进入 $k$ 范围内后算法能够快速地收敛.

以上三类损失函数的图形如下所示.

Fig. 1 三类损失函数与对应的权重函数

---

3. 加权最小二乘

我们先不区别具体的损失函数, 回到线性回归问题 (II-1-1).

一般情况下, 测量数据的组数 $n$ 大于估计变量的维度 $k+1$, 否则就成了欠定问题了.

要使这个回归估计获得最佳的参数估计 ${\mathbf{b}}^{\ast }$, 需要将其转换为如下优化问题
$${\mathbf{b}}^{\ast }=\underset{\mathbf{b}}{\mathrm{argmin}}\sum _{i=1}^n\rho (e_i)=\underset{\mathbf{b}}{\mathrm{argmin}}\sum _{i=1}^n\rho (y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b})\text{\hspace{1em}(II-3-1)}$$
进一步, 求极小值转换为求函数驻点
$$\begin{array}{rl}0& =\frac{\partial \left[{\sum }_{i=1}^n\rho (y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b})\right]}{\partial \mathbf{b}}\\ & =\sum _{i=1}^n\frac{\partial \rho (e_i)}{\partial e_i}\frac{\partial (y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b})}{\partial \mathbf{b}}\\ & =\sum _{i=1}^n\frac{\partial \rho (e_i)}{\partial e_i}{\mathbf{x}}_i^{{}^{\prime }}\end{array}\text{\hspace{1em}(II-3-2)}$$
定义影响曲线 (Influence Curve) 为 $\psi =\rho {}^{\prime }\triangleq \frac{\partial \rho (e_i)}{\partial e_i}$.

定义权重函数 (Weight Function) 为 $w(e_i)\triangleq \frac{\psi (e_i)}{e_i}$. 三类损失函数对应的权重函数如 Fig. 1 所示.

式 (II-3-2) 可改写为
$$\sum _{i=1}^n\underline{w(e_i)}\underline{(y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b})}{\mathbf{x}}_i^{{}^{\prime }}=0\text{\hspace{1em}(II-3-3)}$$

在数值计算中, 将权重函数 $w(e_i)$ 看做是由上一迭代点 $e_i^{[k-1]}$ 计算得到的标量权重值, 而不再视作参数 $\mathbf{b}$ 的函数, 记为 ${\tilde{w}}_i\triangleq w(e_i^{[k]})$.

在上述数值假设下, 式 (II-3-3) 可以进一步写成
$$\sum _{i=1}^n{\tilde{w}}_i(y_i-{\mathbf{x}}_i^{\prime }\mathbf{b}){\mathbf{x}}_i^{\prime }=0\text{\hspace{1em}(II-3-4)}$$
同时, 构造如下加权最小二乘问题
$$\min \frac{1}{2}\sum _{i=1}^n{\tilde{w}}_i{e}_i^2=\min \frac{1}{2}\sum _{i=1}^n{\tilde{w}}_i(y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b}{)}^2\text{\hspace{1em}(II-3-5)}$$
同样求函数极值转变为求驻点
$$\sum _{i=1}^n{\tilde{w}}_i(y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b})\frac{\partial (y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b})}{\partial \mathbf{b}}=\sum _{i=1}^n\underline{{\tilde{w}}_i}\underline{(y_i-{\mathbf{x}}_i^{{}^{\prime }}\mathbf{b})}{\mathbf{x}}_i^{{}^{\prime }}=0\text{\hspace{1em}(II-3-6)}$$
式 (II-3-4) 与式 (II-3-6) 的驻点完全一致, 那么回归问题式 (II-3-1) 与加权最小二乘问题 (II-3-5) 在局部点上等价.

那么由迭代计算式 (II-3-5) 极小值就能获得 (II-3-1) 的极小值. 而应用最小二乘法数值方法迭代求解加权最小二乘问题式 (II-3-5) 的计算方法称为迭代重加权最小二乘法 (Iteratively Reweighted Least Squares, IRLS).

---

III. 鲁棒噪声模型

1. 鲁棒目标函数

对鲁棒回归 (M 估计) 有了基本认识后, 我们再回到噪声模型, 这次需要结合鲁棒回归.

为了减少离群点对因子图最优化目标的影响, 引入鲁棒损失函数 (Robust Loss Function), 比如上文介绍的 Huber Loss.

那么因子图的最小二乘目标就不再适用了, 而变为
$${\Theta }^{\ast }=\underset{\Theta }{\mathrm{argmin}}\sum _i\rho (m_i)\text{\hspace{1em}(III-1-1)}$$
其中 $m_i$ 为马氏距离 (Mahalanobis Distance)
$$m_i\triangleq \sqrt{{\left[h_i({\Theta }_i)-z_i\right]}^{\mathrm{T}}{\Sigma }_i^{-1}\left[h_i({\Theta }_i)-z_i\right]}=\Vert h_i({\Theta }_i)-z_i{\Vert }_{{\Sigma }_i}\text{\hspace{1em}(III-1-2)}$$
对应于式 (II-1-4) 中的残差/误差. 式 (III-1-1) 也可以写成
$${\Theta }^{\ast }=\underset{\Theta }{\mathrm{argmin}}\sum _i\rho (\Vert h_i({\Theta }_i)-z_i{\Vert }_{{\Sigma }_i})\text{\hspace{1em}(III-1-3)}$$

---

2. 非线性加权最小二乘

先对非线性测量误差进行线性化处理
$$\begin{array}{rl}{h}_i({\Theta }_i)-z_i& =h_i({\Theta }_i^{[k-1]}+{\Delta }_i)-z_i\\ & \approx h_i({\Theta }_i^{[k-1]})+H_i{\Delta }_i-z_i\\ & =H_i{\Delta }_i-d_i\end{array}\text{\hspace{1em}(III-2-1)}$$
其中$H_i\triangleq {\frac{\partial h_i({\Theta }_i)}{\partial {\Theta }_i}|}_{{\Theta }_i^{[k-1]}}$, $d_i=z_i-h_i({\Theta }_i^{[k-1]})$. 代入式 (III-1-2) 得到线性化后的马氏距离
$$m_i\approx \Vert H_i{\Delta }_i-d_i{\Vert }_{{\Sigma }_i}=\sqrt{(H_i{\Delta }_i-d_i{)}^{\mathrm{T}}{\Sigma }^{-1}(H_i{\Delta }_i-d_i)}\text{\hspace{1em}(III-2-2)}$$
则
$$m_i^2\approx \Vert H_i{\Delta }_i-d_i{\Vert }_{{\Sigma }_i}^2=(H_i{\Delta }_i-d_i{)}^{\mathrm{T}}{\Sigma }^{-1}(H_i{\Delta }_i-d_i)\text{\hspace{1em}(III-2-3)}$$
线性化后的新变量为 ${\Delta }_i$. 线性化后的优化目标式 (III-1-1) 就变为
$${\Delta }^{\ast }=\underset{\Delta }{\mathrm{argmin}}\sum _i\rho (m_i)\text{\hspace{1em}(III-2-4)}$$
参照上一章节线性回归的推导, 下面简单推导因子图目标函数对应的加权最小二乘目标函数式.

式 (III-2-4) 求极小值就是求对应目标函数的驻点
$$\begin{array}{rl}0& =\frac{\partial \left[{\sum }_i\rho (m_i)\right]}{\partial {\Delta }_i}=\sum _i\frac{\partial \rho (m_i)}{\partial {\Delta }_i}\\ & =\sum _i\frac{\partial \rho (m_i)}{\partial m_i}\frac{\partial m_i}{\partial m_i^2}\frac{\partial m_i^2}{\partial (H_i{\Delta }_i-d_i)}\frac{\partial (H_i{\Delta }_i-d_i)}{\partial {\Delta }_i}\\ & =\sum _i\frac{\partial \rho (m_i)}{\partial m_i}\frac{1}{2m_i}(H_i{\Delta }_i-d_i{)}^{\mathrm{T}}(2{\Sigma }_i^{-1})H_i\\ & =\sum _i\frac{{\rho }^{\prime }(m_i)}{m_i}(H_i{\Delta }_i-d_i{)}^{\mathrm{T}}{\Sigma }_i^{-1}{H}_i\end{array}\text{\hspace{1em}(III-2-5)}$$
其中 ${\rho }^{\prime }(m_i)=\frac{\partial \rho (m_i)}{\partial m_i}$, 另外计算中用到 [Identity 8-b] Partial Derivative of a Quadratic Form (Numerator-Layout Notation).

构造等价的加权最小二乘问题
$$\underset{\Delta }{\mathrm{argmin}}\frac{1}{2}\sum _i\frac{{\rho }^{\prime }(m_i^{[k-1]})}{m_i^{[k-1]}}\Vert H_i{\Delta }_i-d_i{\Vert }_{{\Sigma }_i}^2\text{\hspace{1em}(III-2-6)}$$
其中 $m_i^{[k-1]}$ 是迭代计算中上一迭代步中已确定了 $m_i$ 标量值.

求式 (III-2-6) 中目标函数的驻点
$$\begin{array}{rl}0& =\frac{1}{2}\sum _i\frac{{\rho }^{\prime }(m_i^{[k-1]})}{m_i^{[k-1]}}\frac{\partial \Vert H_i{\Delta }_i-d_i{\Vert }_{{\Sigma }_i}^2}{\partial {\Delta }_i}\\ & =\sum _i\frac{{\rho }^{\prime }(m_i^{[k-1]})}{m_i^{[k-1]}}(H_i{\Delta }_i-d_i{)}^{\mathrm{T}}{\Sigma }_i^{-1}{H}_i\end{array}\text{\hspace{1em}(III-2-7)}$$
比较式 (III-2-5) 和式 (III-2-7), 可知在 $m_i^{[k-1]}$ 时两者驻点一致, 就是式 (III-2-4) 和式 (III-2-6) 的最优目标在 $m_i^{[k-1]}$ 时等价 (一致).

我们每一步迭代计算式 (III-2-6) 的优化值, 就是在求线性化后的因子图目标函数的优化值, 作为原始非线性因子图目标函数 (III-1-1) 的优化值的增量更新.

也就是说, 我们为了防止离群点污染优化目标而引入鲁棒损失函数后, 一样有办法计算因子图的优化值.

---

3. 迭代重加权最小二乘法

基于上面的鲁棒噪声模型、加权最小二乘问题等推导, 我们就可以理解的针对因子图的迭代重加权最小二乘法.

算法: 针对非线性鲁棒噪声问题的非线性信赖域方法^[1]

设置变量初始值 $\Theta$

while (迭代未收敛) do

  计算每一个因子误差的马氏距离 $m_i^{[k-1]}=\Vert h_i(x_i^{[k-1]})-z_i{\Vert }_{{\Sigma }_i}$

  计算每一个因子的权重 ${\tilde{w}}_i={\rho }^{\prime }(m_i^{[k-1]})/m_i^{[k-1]}$

  构造加权最小二乘问题 $\frac{1}{2}{\sum }_i{\tilde{w}}_i\Vert h_i({\Theta }_i)-z_i{\Vert }_{{\Sigma }_i}^2$

  线性化最小二乘问题得到 $\frac{1}{2}{\sum }_i{\tilde{w}}_i\Vert H_i{\Delta }_i-d_i{\Vert }_{{\Sigma }_i}^2$

  解线性化最小二乘问题

  维持信赖域

  基于列文伯格-马夸尔特法或狗腿法更新 $\Theta$

end

---

V. 总结

本文介绍了因子图计算中的鲁棒噪声模型、鲁棒参数估计、M-估计、非线性加权最小二乘问题、迭代重加权最小二乘法等.

主要围绕因子图计算中的离群点抑制以获得不受污染的优化估计——这一关键目标进行叙述和推导.

(如有问题请指出, 谢谢！)

---

参考文献

[1] Fan Jiang, Yetong Zhang, “GTSAM Robust Noise Model”, https://github.com/borglab/gtsam/blob/develop/doc/robust.pdf, 2020.02

[2] Frank Dellaert, Michael Kaess, “Factor Graphs for Robot Perception”, Foundations and Trends in Robotics, Vol. 6, No. 1-2 (2017) 1–139

[3] Jing Dong, “GTSAM 4.0 Tutorial —— Theory, Programming, and Applications”, https://dongjing3309.github.io/files/gtsam-tutorial.pdf, 2016.11.19

[4] John Fox, Sanford Weisberg, “Robust Regression”, http://users.stat.umn.edu/~sandy/courses/8053/handouts/robust.pdf, 2013.10.08

[5] 俞搏天, “p-Huber 损失函数及其鲁棒性研究”, 应用数学进展, 9(12): 2283-2291, 2020