为什么要重装,是想在mac电脑 创建data目录…同事误操作,导致电脑重启不了.然后重装系统后,.就连不上数据库了.mysql和pgsql两个都连不上.网上也查了很多资料.实在不行,.就重装了…
重装mysql.
1.官网下载
https://www.mysql.com/downloads/
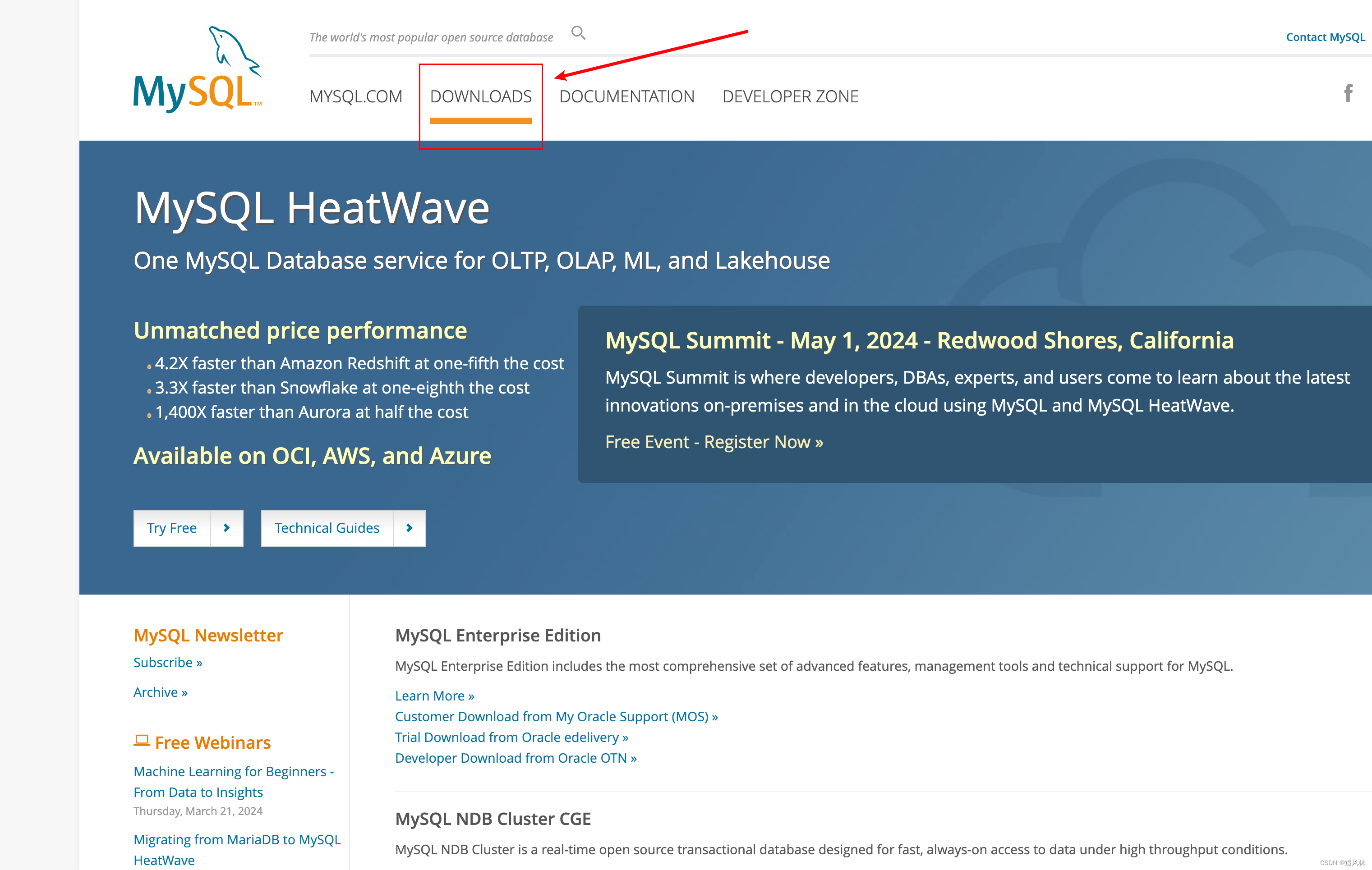
滑到最下面 选择
选择对应的芯片版本
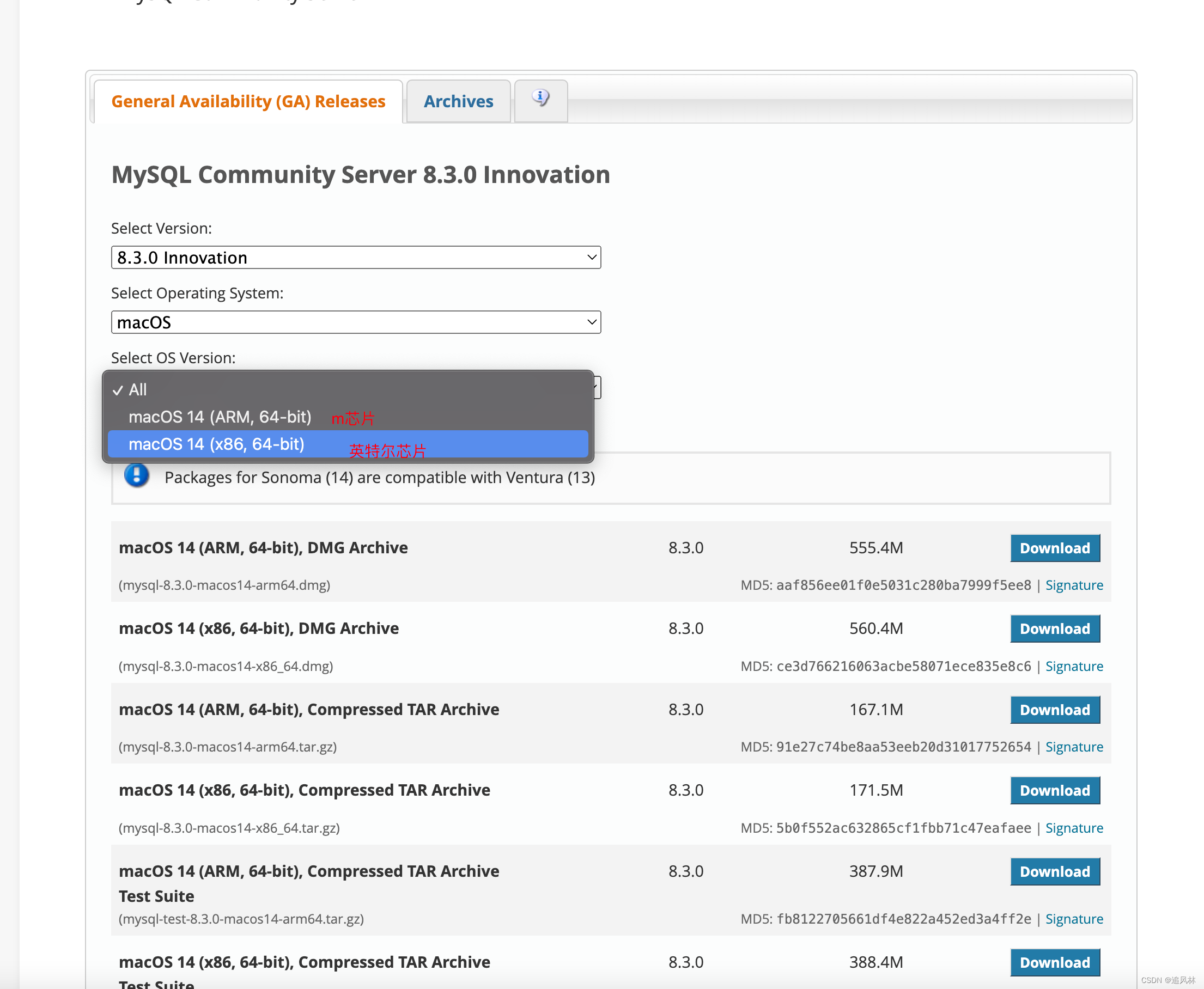
然后下载下来点击安装.一直安装就好
安装完过后,.设置里面一直没有图标出俩. 折腾了半天…重启就好了…
重装pgsql///
官网下载,安装包. https://www.postgresql.org/
傻瓜式下一步…就可以; 记住账号密码.
坑点:我之前安装的15的.我这次也是下载的15版本的.下载下来,一直连接不上.解决不了.折腾了一下午.换了个低版本.一遍流程就连接上了…坑了我一天…难受
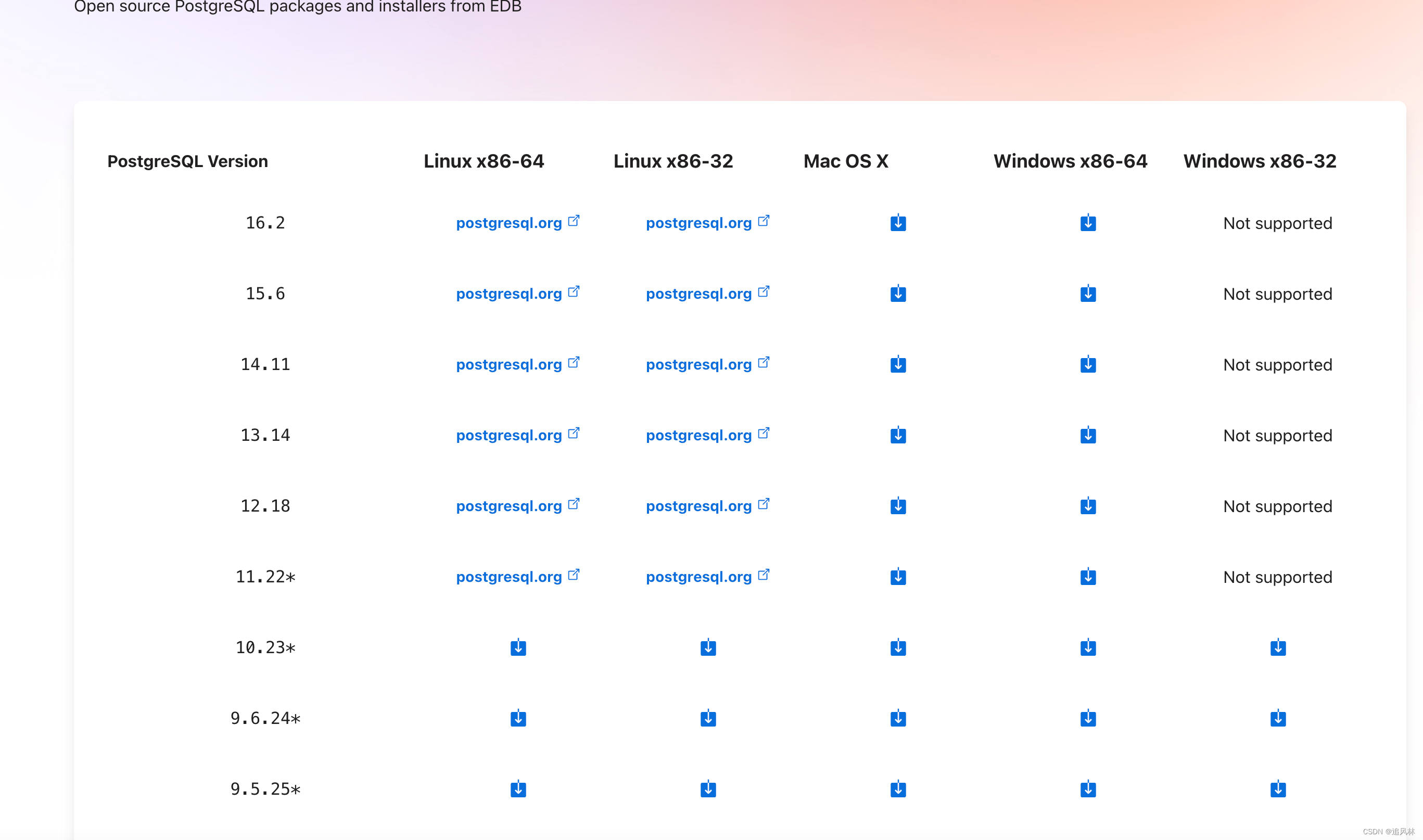
傻瓜安装…要你设置账号和密码,端口就设置.然后自己记住就好了