L1 loss

均绝对误差（Mean Absolute Error，MAE），公式如下

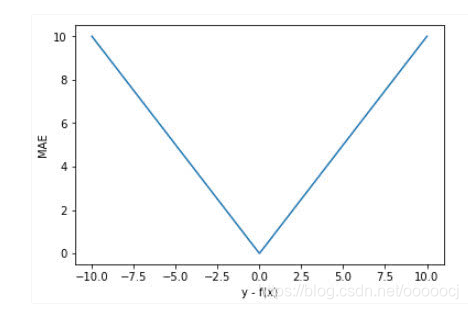
优点：因为梯度不变，对离群点不敏感

缺点：因为梯度不变，不管是误差小还是大，梯度都一样，不利于模型收敛。

L2 loss

均方误差（Mean Square Error，MSE），公式如下

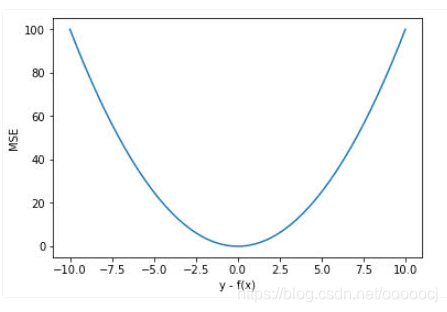
优点：训练初期误差大，梯度也大，有利于快速收敛。后期误差小，梯度也小，有利于模型的稳定。

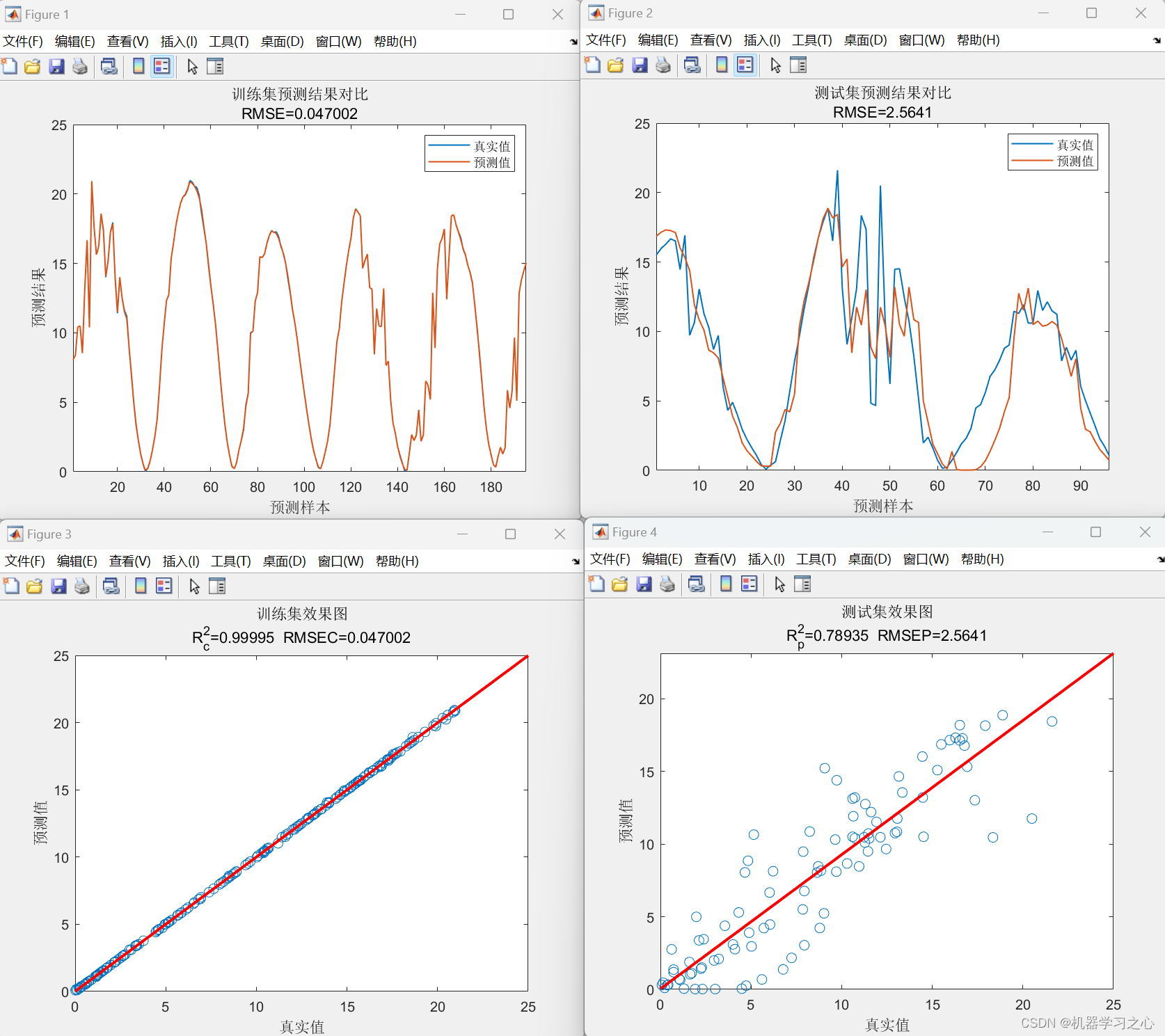
缺点：梯度是误差的2倍，对于离群点，误差极大梯度也大，模型对离群点敏感，受其影响较大，模型给离群点较大的权重，可能会往离群点方向偏移，导致牺牲正常点的预测效果，最终降低模型的整体性能。如下图

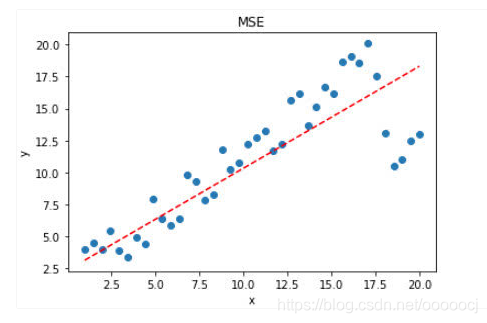
作为对比，L1的预测效果如下，可以看出，L1 loss对离群点的抗干扰能力更强

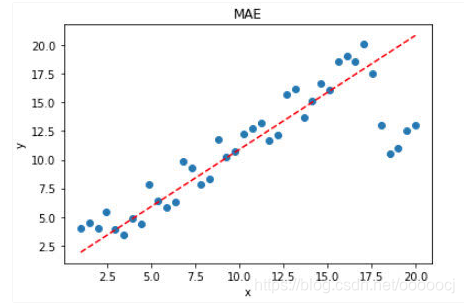
Smooth L1 loss

在Faster-RCNN和SSD中对边框的回归使用的都是Smooth L1损失，公式如下

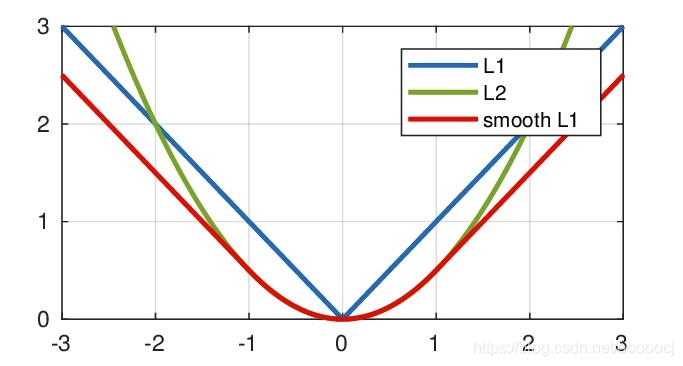
结合了L1不易受离群点干扰的优点以及L2在误差较小时梯度也小，学习率不变时可以继续收敛到更高精度的有点，而不像L1在误差小时梯度也为1，从而在稳定值附近波动，难以继续收敛。

参考

https://www.cnblogs.com/wangguchangqing/p/12021638.html

请问 faster RCNN 和 SSD 中为什么用smooth L1 loss，和L2有什么区别？ - 知乎