实验三
(实验报告中附上每题的主要程序和结果)
1、在命令行窗口中分别输入下列命令,对应输出结果是
A.命令x=[-2:2]
B.命令x=zeros(1,2);x>=0
C.命令y=diag(eye(3),1)
D.命令[-2:2]+30*eye(size([-2:2]))
>> x=[-2:2]
x =
-2 -1 0 1 2
>> x=zeros(1,2);x>=0
ans =
1 1
>> y=diag(eye(3),1)
y =
0
0
>> [-2:2]+30*eye(size([-2:2]))
ans =
28 -1 0 1 2
% D = diag(v,k) 将向量 v 的元素放置在第 k 条对角线上。k=0 表示主对角线,k>0 位于主对角线上方,k<0 位于主对角线下方。
>> a=eye(3)
a =
Diagonal Matrix
1 0 0
0 1 0
0 0 1
>> diag(a)
ans =
1
1
1
>> diag(a,1)
ans =
0
0
>> diag(a,2)
ans = 0
>> diag(a,-1)
ans =
0
0
>> diag(a,-2)
ans = 0
2、
1)产生一个全0的10阶矩阵a,置a的3行4列元素为4,语句是 ______ 。
2)产生一个-1~1之间均匀分布的3阶随机矩阵a,并求它的逆矩阵b。语句是 _____ 。
% 产生一个全0的10阶矩阵a,置a的3行4列元素为4
>> a=zeros(10)
a =
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
>> a(3,4)=4
a =
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 4 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0 0
% 产生一个-1~1之间均匀分布的3阶随机矩阵a,并求它的逆矩阵b
>> a=(rand(3,3)-rand(3,3))
a =
-0.746305 0.090700 0.346483
-0.873974 0.516029 0.240872
-0.087227 0.495974 -0.083827
>> b=inv(a)
b =
7.4979 -8.2686 7.2318
4.3439 -4.2752 5.6700
17.8991 -16.6909 14.0926
3、按要求编写fun函数
函数输入参数:一个向量
函数输出参数:该向量中所有大于0的奇数元素的和
功能:求该向量中所有大于0的奇数元素的和
函数调用示例:s=fun([-1, 0, 2, 3, -5, 4])
% 方法一
function y=fun(a)
y=sum(a(rem(a,2)==1));
end
>> s=fun([-1,0,2,3,-5,4])
s = 3
%方法二
function x=fun(X)
x=0;
for i=1:length(X)
if mod(X(i),2)!=0 && X(i)>0
x=x+X(i);
endif
endfor
end
>> s=fun([-1,0,2,3,-5,4])
s = 3
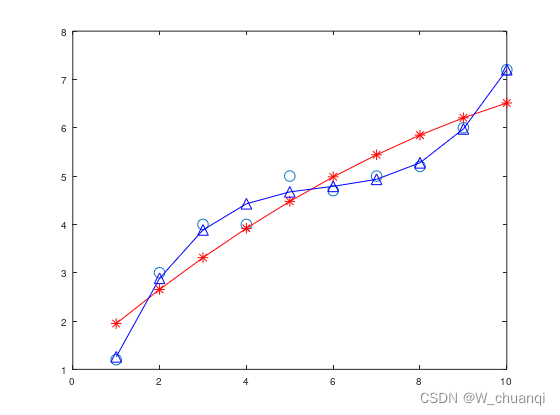
4、考虑如下一组实验数据:
X=[1, 2, 3, 4, 5, 6, 7, 8, 9, 10]
Y=[1.2, 3, 4, 4 ,5, 4.7, 5, 5.2, 6, 7.2]
请用最小二乘法对该数据分别拟合一个二次和三次多项式函数曲线
在同一窗口绘出拟合曲线,并计算拟合误差。(请给出解题步骤)
x=[1,2,3,4,5,6,7,8,9,10];
y=[1.2, 3, 4, 4 ,5, 4.7, 5, 5.2, 6, 7.2];
plot(x,y,'o')
hold on
%二次函数拟合
p1=polyfit(x,y,2);
y1=p1(1)*x.*x+p1(2)*x+p1(3);
plot(x,y1,'r-*')
hold on
%二次函数拟合误差
%SSE(和方差)计算拟合数据和原始数据对应点的误差的平方和,SSE越趋近于0,
%说明模型选择和拟合更好,数据预测也越成功
SSE1=sum((y-y1).^2)/length(x)
%三次函数拟合
p2=polyfit(x,y,3);
y2=p2(1)*x.^3+p2(2)*x.*x+p2(3)*x+p2(4);
plot(x,y2,'b-^')
%三次函数拟合误差
SSE2=sum((y-y2).^2)/length(x)
运行结果:
>> polyfit1
SSE1 = 0.2642
SSE2 = 0.033763
5、
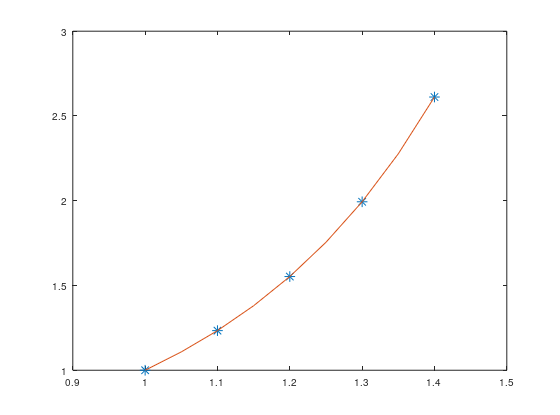
5.1、有如下数据:
x 1 1.1 1.2 1.3 1.4
y 1.00000 1.23368 1.55271 1.99372 2.61170
利用spline插值方法对其进行插值,得到每隔0.05的结果。
x=[1,1.1,1.2,1.3,1.4];
y=[1.00000,1.23368,1.55271,1.99372,2.61170];
plot(x,y,'*')
hold on;
x_spline=[1:0.05:1.4];
y_spline=interp1(x,y,x_spline,'spline');
plot(x_spline,y_spline,'-')
运行结果:
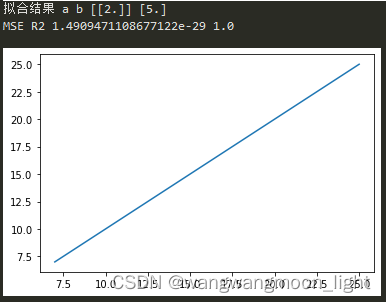
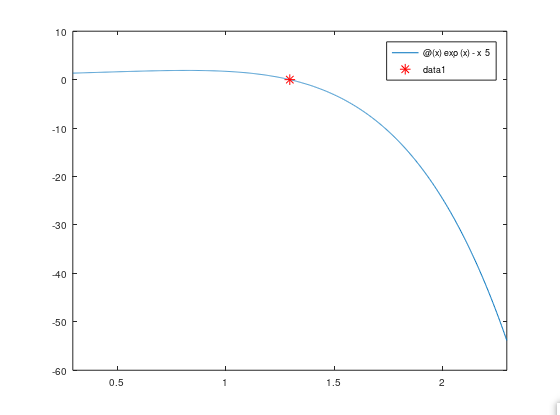
5.2、求函数 y=ex-x5,初始点为x=8的解,并绘制图形。
y=@(x)exp(x)-x^5;
x = fzero(y,8);
fplot(y,[x-1,x+1]);
hold on
plot(x,y(x),'r*');
输出结果为:
5.3、求下列函数的极值。
(1)z=x2-(y-1)2
z = @(x)x(1)^2-(x(2)-1)^2;
[x,fvalue,flag,output]=fminsearch(z,[0,0])
输出结果为:

(2)z=(x-y+1)2
>> z = @(x)(x(1)-x(2)+1)^2;
>> [x,fvalue,flag,output]=fminsearch(z,[0,0])
输出结果为: