1.1 回归分析

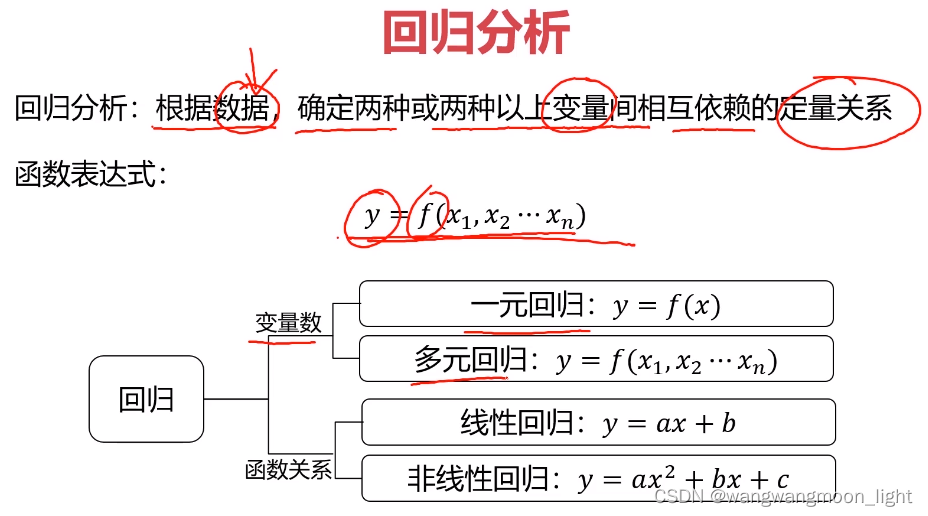
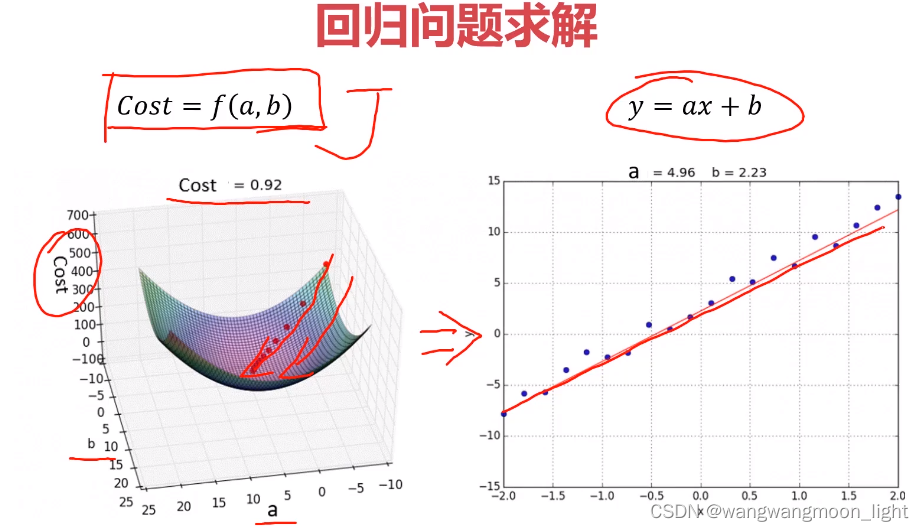
在这里插入图片描述

1.2 线性回归问题求解

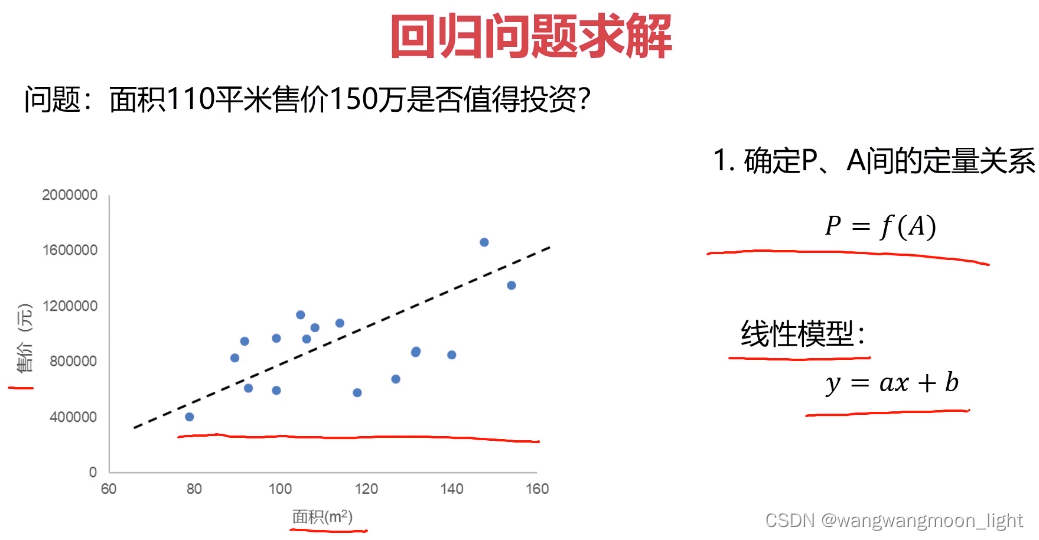
在这里插入图片描述

1.3 寻找最合适的 a、b，引入损失函数的概念

尽可能使损失函数最小即找到了最合适的 a、b
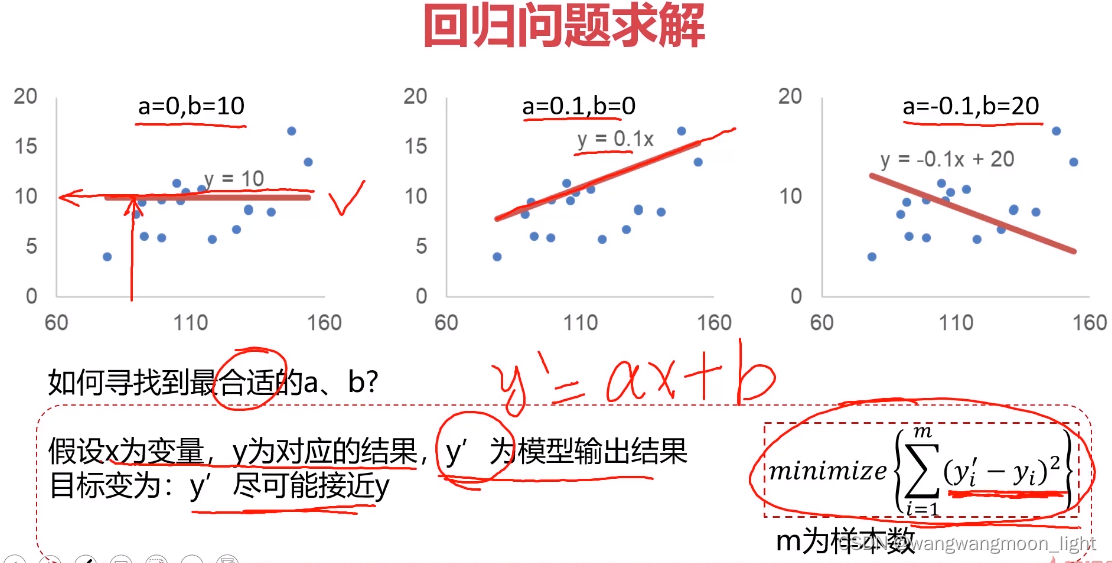
![](https://img-blog.csdnimg.cn/a251f3cf46bf4721bd906a31c2e8993f.png)

1.4 损失函数的计算

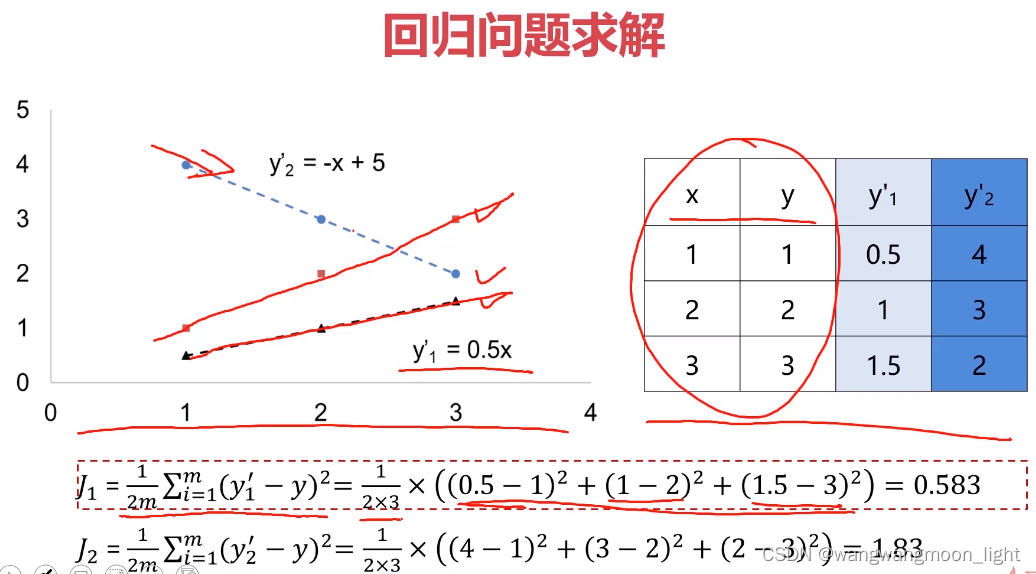
在这里插入图片描述

1.5 怎么找a b 值呢，使用梯度下降法

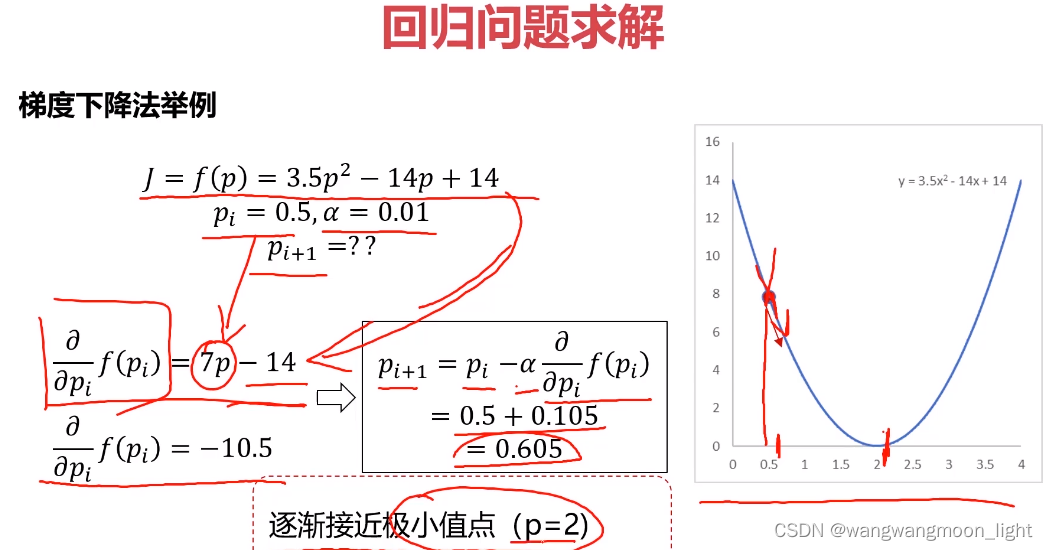
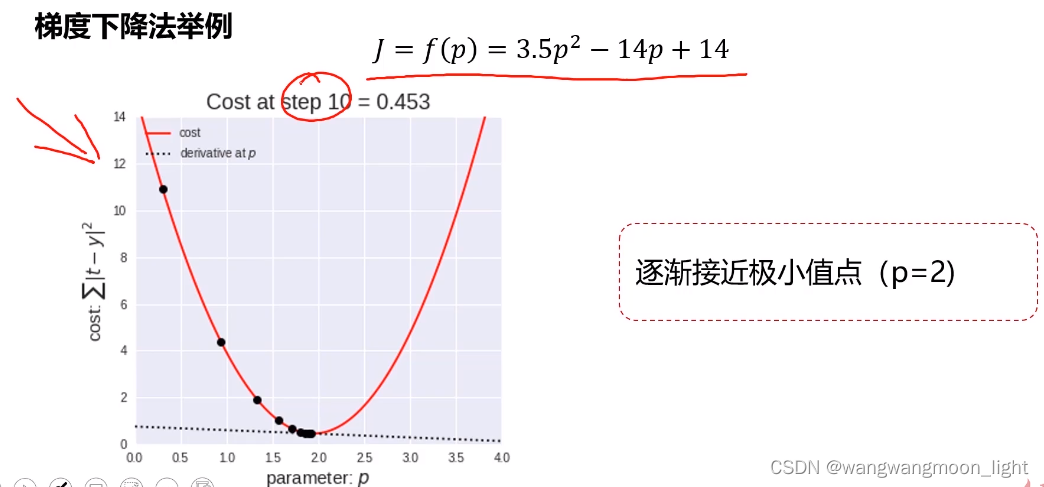
在这里插入图片描述

1.6 怎么利用梯度下降法找 a 、b值呢

在这里插入图片描述

--------------------------------------------------------分割线------------------------------------------------

2. 任务:

步骤：
1）使用模型预测合理房价，根据预测结果做出判断
2）生成损失函数
3）选择回归模型
4）使用梯度下降或者其他方法求解最小化损失函数的模型参数

2.1 Sklearn包介绍

42.png)

2.2 使用Sklearn求解a、b值

基于generated_data.csv数据，建立线性回归模型，预测x=3.5对应的y值，评估模型表现

generated_data.csv数据如下：
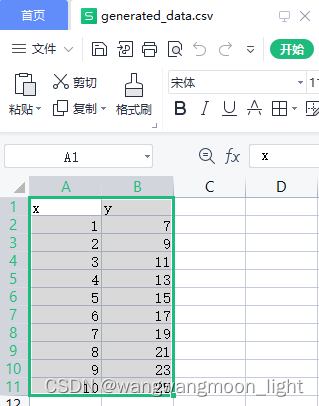
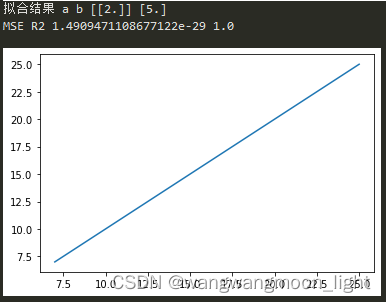
在这里插入图片描述
拟合结果： y = 2x + 5

## 回归分析 -- 房价 = F(面积)
import pandas as pd
import numpy as np
from matplotlib import pyplot as plt
from sklearn.linear_model import LinearRegression
from sklearn.metrics import mean_squared_error,r2_score

data = pd.read_csv('generated_data.csv')
data.head()
x = data.loc[:,'x']
y = data.loc[:,'y']
#print("原始输入 x, y", x, y)
plt.figure(figsize=(20,20))
plt.scatter(x,y)
plt.show()
lr_model = LinearRegression()
x = np.array(x)
x = x.reshape(-1,1)
y = np.array(y)
y = y.reshape(-1,1)
# print(type(x),x.shape,type(y),y.shape)
# print(type(x),x.shape)
lr_model.fit(x,y)
a = lr_model.coef_
b = lr_model.intercept_
print("拟合结果 a b", a, b)
# 对新数据3.5进行预测
y_3 = lr_model.predict([[3.5]])
#print(y_3)
#print(y)
# 模型均方误差评估
y_predict = lr_model.predict(x)
#print("y_predict", y_predict)
# MSE越小越好，R2越接近1越好
MSE = mean_squared_error(y,y_predict)
R2 = r2_score(y,y_predict)
print("MSE R2", MSE, R2)
plt.figure()
plt.plot(y, y_predict)
plt.show()