自己动手写编译器:从NFA到DFA

news2024/10/6 8:21:57

上一节我们完成了使用NFA来识别字符串的功能。NFA有个问题就是其状态节点太多，使用起来效率不够好。本节我们介绍一种叫“子集构造”的算法，将拥有多个节点的NFA转化为DFA。在上一节我们描述的epsilon闭包操作可以看到，实际上所有由epsilon边连接在一起的节点其实都能看作是一个状态节点，由此我们就能通过epsilon操作将多个节点转化为一个DFA节点，同时epsilon闭包操作所得的节点集合中，每一个节点发出的边都可以看作是新DFA节点发出的边。

我们用上一节完成的NFA状态机来看看具体过程：
​​​​在这里插入图片描述
从节点0开始做epsilon操作所得结果为：
epsilon-closure(0) = {0, 27, 11, 19, 9, 12, 13}, 由此我们把这些节点合成一个新节点，我们标记为DFA state 0。

接着我们对集合{0, 27, 11, 19, 9, 12}做move操作有：
move({0, 27, 11, 19, 9, 12, 14}, D} = {10, 20}, 于是可以把节点10，20合成新节点，记做"DFA state 1", 因为有:
move({0, 27, 11, 19, 9, 12}, .} = {14}, 于是我们把节点14看做新节点，记做"DFA state 2"，这么一来我们就得到如下DFA状态机：
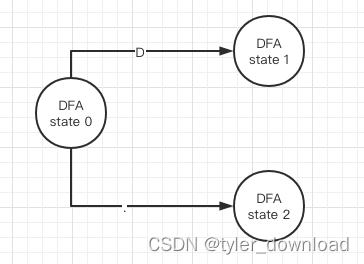
请添加图片描述
接下来我们继续对{10, 20}进行epsilon闭包操作，epsilon-closure({10, 20})={10, 20, 9,12,13,21}，然后再对这个结果做move操作有:
move({10, 20, 9,12,13,21}, D) = {10} , 于是我们再产生一个新DFA节点记作DFA state 3, move({10, 20, 9,12,13,21}, . } = {14, 22} 于是我们再产生新的DFA节点记作DFA state 4,于是就有:
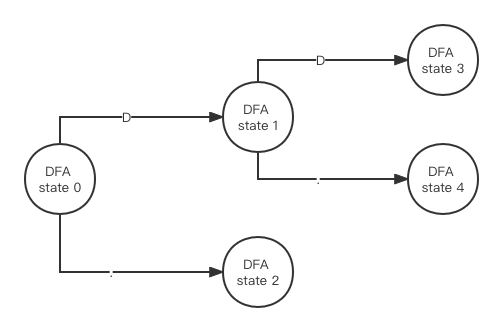
请添加图片描述
这个过程以此类推，这里需要注意的是如果epsilon闭包操作后所得的节点集合中有NFA状态机的终结节点，那么其对应的DFA节点就是一个终结节点。接下来看看代码如何实现，我们添加一个名为nfa_to_dfa.go的文件，然后添加代码如下：

import "fmt"

const (
	DFA_MAX   = 254 //DFA 最多节点数
	F         = -1  //用于初始化跳转表
	MAX_CHARS = 128 //128个ascii字符
)

type ACCEPT struct {
	acceptString string //接收节点对应的执行代码字符串
	anchor       Anchor
}

type DFA struct {
	group        int  //后面执行最小化算法时有用
	mark         bool //当前节点是否已经设置好接收字符对应的边
	anchor       Anchor
	set          []*NFA //dfa节点对应的nfa节点集合
	state        int    //dfa 节点号码
	acceptString string
}

这里我们先定义基本的数据结构，在转换的DFA状态机中，它最多包含254个节点，同时状态机只接收来自ascii表中数值从0到128的字符，这次我们构造的DFA状态机将不像上次构造的NFA状态机那样使用链表结构，这次我们使用跳转表结构，我们将构造一个二维数组dtrans，假设状态节点1接收字符“.“后，跳转到状态节点2，由于字符”."对应的ascii数值为46，那么就有dtrans[1][46] = 2.

在上面代码中我们定义了DFA节点，由于一个DFA节点由一组NFA节点转换而来，因此在它的定义中有一个NFA节点的指针数组。接下来我们设计用于将NFA转换成DFA的类，其代码为：

type NfaDfaConverter struct {
	nstates    int     //当前dfa 节点计数
	lastMarked int     //下一个需要处理的dfa节点
	dtrans     [][]int //dfa状态机的跳转表
	accepts    []*ACCEPT
	dstates    []DFA //所有dfa节点的集合
}

func NewNfaDfaConverter() *NfaDfaConverter {
	n := &NfaDfaConverter{
		nstates:    0,
		lastMarked: 0,
		dtrans:     make([][]int, DFA_MAX),
		dstates:    make([]DFA, DFA_MAX),
	}

	for i := range n.dtrans {
		n.dtrans[i] = make([]int, MAX_CHARS)
	}

	return n
}

在定义中有几个变量需要注意，其中dtrans是用于构造DFA跳转表的二维数组， nstates用于记录当前已经生成的DFA节点数量，lastMarked用于指向下一个要创建其跳转逻辑的DFA节点编号，dstates用于存储当前已经创建了的DFA节点。下面我们看看转换逻辑的实现:

func (n *NfaDfaConverter) getUnMarked() *DFA {
	for ; n.lastMarked < n.nstates; n.lastMarked++ {
		debug := 0
		if n.dstates[n.lastMarked].state == 5 {
			debug = 1
			fmt.Printf("debug: %d", debug)
		}
		if n.dstates[n.lastMarked].mark == false {
			return &n.dstates[n.lastMarked]
		}
	}

	return nil
}

func (n *NfaDfaConverter) compareNfaSlice(setOne []*NFA, setTwo []*NFA) bool {
	//比较两个集合的元素是否相同
	if len(setOne) != len(setTwo) {
		return false
	}

	equal := false
	for _, nfaOne := range setOne {
		for _, nfaTwo := range setTwo {
			if nfaTwo == nfaOne {
				equal = true
				break
			}
		}

		if equal != true {
			return false
		}
	}

	return true
}

func (n *NfaDfaConverter) hasDfaContainsNfa(nfaSet []*NFA) (bool, int) {
	//查看是否存在dfa节点它对应的nfa节点集合与输入的集合相同
	for _, dfa := range n.dstates {
		if n.compareNfaSlice(dfa.set, nfaSet) == true {
			return true, dfa.state
		}
	}

	return false, -1
}

func (n *NfaDfaConverter) addDfaState(epsilonResult *EpsilonResult) int {
	//根据当前nfa节点集合构造一个新的dfa节点
	nextState := F
	if n.nstates >= DFA_MAX {
		panic("Too many DFA states")
	}

	nextState = n.nstates
	n.nstates += 1
	n.dstates[nextState].set = epsilonResult.results
	n.dstates[nextState].mark = false
	n.dstates[nextState].acceptString = epsilonResult.acceptStr
	n.dstates[nextState].anchor = epsilonResult.anchor
	n.dstates[nextState].state = nextState //记录当前dfa节点的编号s

	n.printDFAState(&n.dstates[nextState])
	fmt.Print("\n")

	return nextState
}

func (n *NfaDfaConverter) printDFAState(dfa *DFA) {
	fmt.Printf("DFA state : %d, it is nfa are: {", dfa.state)
	for _, nfa := range dfa.set {
		fmt.Printf("%d,", nfa.state)
	}

	fmt.Printf("}")
}

func (n *NfaDfaConverter) MakeDTran(start *NFA) {
	//根据输入的nfa状态机起始节点构造dfa状态机的跳转表
	startStates := make([]*NFA, 0)
	startStates = append(startStates, start)
	statesCopied := make([]*NFA, len(startStates))
	copy(statesCopied, startStates)

	//先根据起始状态的求Epsilon闭包操作的结果，由此获得第一个dfa节点
	epsilonResult := EpsilonClosure(statesCopied)
	n.dstates[0].set = epsilonResult.results
	n.dstates[0].anchor = epsilonResult.anchor
	n.dstates[0].acceptString = epsilonResult.acceptStr
	n.dstates[0].mark = false

	//debug purpose
	n.printDFAState(&n.dstates[0])
	fmt.Print("\n")
	nextState := 0
	n.nstates = 1 //当前已经有一个dfa节点
	//先获得第一个没有设置其跳转边的dfa节点
	current := n.getUnMarked()
	for current != nil {
		current.mark = true
		for c := 0; c < MAX_CHARS; c++ {
			nfaSet := move(current.set, c)
			if len(nfaSet) > 0 {
				statesCopied = make([]*NFA, len(nfaSet))
				copy(statesCopied, nfaSet)
				epsilonResult = EpsilonClosure(statesCopied)
				nfaSet = epsilonResult.results
			}

			if len(nfaSet) == 0 {
				nextState = F
			} else {
				//如果当前没有那个dfa节点对应的nfa节点集合和当前nfaSet相同，那么就增加一个新的dfa节点
				isExist, state := n.hasDfaContainsNfa(nfaSet)
				if isExist == false {
					nextState = n.addDfaState(epsilonResult)
				} else {
					nextState = state
				}
			}

			//设置dfa跳转表
			n.dtrans[current.state][c] = nextState
		}

		current = n.getUnMarked()
	}
}

func (n *NfaDfaConverter) PrintDfaTransition() {
	for i := 0; i < DFA_MAX; i++ {
		if n.dstates[i].mark == false {
			break
		}

		for j := 0; j < MAX_CHARS; j++ {
			if n.dtrans[i][j] != F {
				n.printDFAState(&n.dstates[i])
				fmt.Print(" jump to : ")
				n.printDFAState(&n.dstates[n.dtrans[i][j]])
				fmt.Printf("by character %s\n", string(j))
			}
		}
	}
}

前面我们看到，一个DFA节点本质上对应一组NFA节点，因此当我们使用move 和epsilon闭包操作得到一组NFA节点后，我们需要看看是不是已经有DFA节点对应到了生成的NFA节点集合，如果有了，说明对应的DFA节点已经生成，这个操作由函数compareNfaSlice和hasDfaContainsNfa完成，如果当前得到的NFA节点集合没有对应的DFA节点，那么就使用addDfaState函数去创建一个新的DFA节点，然后将其加入到dstates数组中。

每新建一个DFA节点时，它的mark标志位会设置成false,这表明我们还没有为它设置跳转边，函数getUnMarked用于将当前所有mark设置为false的DFA节点中找出创建时间最早的那个。上面代码的算法核心在函数MakeDTran,它执行了我们上面提到的算法，首先获得NFA状态机的起始节点，然后通过epsilon闭包操作获得一组NFA节点，用这组节点创建一个对应的DFA节点。接着使用move操作得到第二组NFA节点，然后再次使用epsilon闭包操作获得新一组NFA节点，然后创建第二个DFA节点，最后根据这两个节点对应的编号在二维表dtrans中设置跳转逻辑。

接下来我们在主函数中调用上面实现代码看看结果，在mai.go中输入代码如下：

package main

import (
	"nfa"
)

func main() {
	lexReader, _ := nfa.NewLexReader("input.lex", "output.py")
	lexReader.Head()
	parser, _ := nfa.NewRegParser(lexReader)
	start := parser.Parse()
	parser.PrintNFA(start)
	//str := "3.14"
	//if nfa.NfaMatchString(start, str) {
	//	fmt.Printf("string %s is accepted by given regular expression\n", str)
	//}
	nfaConverter := nfa.NewNfaDfaConverter()
	nfaConverter.MakeDTran(start)
	nfaConverter.PrintDfaTransition()
}

上面代码运行后输出结果如下:

DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,}
DFA state : 1, it is nfa are: {14,15,}
DFA state : 2, it is nfa are: {10,9,12,13,20,21,}
DFA state : 3, it is nfa are: {16,28,}
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,}
DFA state : 5, it is nfa are: {10,9,12,13,}
DFA state : 6, it is nfa are: {16,28,24,23,26,28,}
DFA state : 7, it is nfa are: {24,23,26,28,}
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 1, it is nfa are: {14,15,}by character .
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 0
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 1
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 2
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 3
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 4
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 5
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 6
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 7
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 8
DFA state : 0, it is nfa are: {0,27,19,11,12,13,9,} jump to : DFA state : 2, it is nfa are: {10,9,12,13,20,21,}by character 9
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 0
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 1
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 2
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 3
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 4
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 5
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 6
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 7
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 8
DFA state : 1, it is nfa are: {14,15,} jump to : DFA state : 3, it is nfa are: {16,28,}by character 9
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,}by character .
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 0
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 1
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 2
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 3
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 4
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 5
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 6
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 7
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 8
DFA state : 2, it is nfa are: {10,9,12,13,20,21,} jump to : DFA state : 5, it is nfa are: {10,9,12,13,}by character 9
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 0
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 1
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 2
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 3
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 4
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 5
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 6
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 7
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 8
DFA state : 4, it is nfa are: {22,25,26,28,23,14,15,} jump to : DFA state : 6, it is nfa are: {16,28,24,23,26,28,}by character 9
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 0
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 1
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 2
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 3
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 4
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 5
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 6
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 7
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 8
DFA state : 6, it is nfa are: {16,28,24,23,26,28,} jump to : DFA state : 7, it is nfa are: {24,23,26,28,}by character 9

我们将上面输出绘制成图形如下：
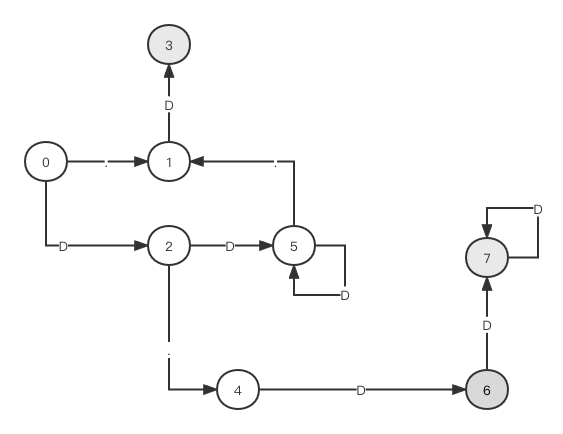
请添加图片描述

对比上面的NFA状态图，DFA状态图就要简单很多，此外生成的DFA状态机还可以继续精简，下一节我们再看看相关算法。代码下载地址为：链接: https://pan.baidu.com/s/1kStrJMznrexQkGGBs8vN3w 提取码: dqss

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/146975.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

「ARM32」MMU和页表的映射过程详解

「ARM32」MMU和页表的映射过程详解

在ARM32中&#xff0c;MMU主要完成虚拟地址到物理地址的映射&#xff0c;并且能够控制内存的访问权限&#xff0c;而页表是实现上述功能的主要手段。页表又分为一级页表、二级页表&#xff0c;在ARM64中甚至还有三级页表。为了便于理解&#xff0c;本章主要讲述一级页表完成段映…
阅读更多...
centos7 安装Mysql详细教程

centos7 安装Mysql详细教程

centos7 弃用了Mysql&#xff0c;默认安装了MariaDB&#xff0c;MariaDB是Mysql一个分支&#xff0c;所以要想在centos上安装Mysql&#xff0c;需要先进行卸载MariaDB&#xff0c;避免冲突 本次教程所用环境&#xff1a; 腾讯云服务器&#xff1a;centos7Mysql5.7 1. 卸载Ma…
阅读更多...
dubbo源码实践-protocol层-invoker理解

dubbo源码实践-protocol层-invoker理解

1概述Invoker官方解释&#xff1a;Invoker 是实体域&#xff0c;它是 Dubbo 的核心模型&#xff0c;其它模型都向它靠扰&#xff0c;或转换成它&#xff0c;它代表一个可执行体&#xff0c;可向它发起 invoke 调用&#xff0c;它有可能是一个本地的实现&#xff0c;也可能是一个…
阅读更多...
Python 机器学习最常打交道的 27 款工具包

Python 机器学习最常打交道的 27 款工具包

为了大家能够对人工智能常用的 Python 库有一个初步的了解&#xff0c;以选择能够满足自己需求的库进行学习&#xff0c;对目前较为常见的人工智能库进行简要全面的介绍。 1、Numpy NumPy(Numerical Python)是 Python的一个扩展程序库&#xff0c;支持大量的维度数组与矩阵运算…
阅读更多...
Maix Bit（K210）保姆级入门上手教程

Maix Bit（K210）保姆级入门上手教程

Maix Bit&#xff08;K210&#xff09;快速上手 这是K210快速上手系列文章&#xff0c;主要内容是&#xff0c;设备连接&#xff0c;环境准备&#xff0c;运行第一个程序 阅读文章前提&#xff1a;python基础,K210是使用Micropython脚本语法的&#xff0c;因此需要一些python…
阅读更多...
RocketMQ5.0.0部署与实例

RocketMQ5.0.0部署与实例

一、Idea调试1.相关配置文件在E:\rocketmq创建conf、logs、store三个文件夹。从RocketMQ distribution部署目录中将broker.conf、logback_namesrv.xml、logback_broker.xml文件复制到conf目录。如下图所示。其中logback_namesrv.xml、logback_broker.xml分别是NameServer、Brok…
阅读更多...
纯C语言实现动态爱心（详解，初学者也能看懂）

纯C语言实现动态爱心（详解，初学者也能看懂）

文章目录✍动态爱心实现&#x1f496;一段小故事&#xff1a;爱心函数的由来&#x1f388; 创建动态爱心的准备&#xff08;非小白可以跳过&#xff09;1.爱心字符2.对easyx库里面的基础函数的认识①initgraph函数②settextcolor、settextstyle、setbkmode、outtextxy四种函数③…
阅读更多...
PostgresSQL数据库的使用

PostgresSQL数据库的使用

PostgresSQL数据库的使用 下载安装 数据类型 使用指导 数据库操作 连接控制台 psql -h <实例连接地址> -U <用户名> -p <端口号>参数描述实例连接地址RDS PostgreSQL实例的连接地址&#xff0c;本机可用localhost或者127.0.0.1用户名创建的RDS Postgre…
阅读更多...
ES语法扩展

ES语法扩展

剩余参数 剩余参数本质 // 剩余参数的本质const add(x,y,...args)>{console.log(x,y,args);}add();add(1);add(1,2);add(1,2,3,4,5); 剩余参数的注意事项 箭头函数的参数部分即使只有一个剩余参数&#xff0c;也不能省略圆括号使用剩余参数替代arguments获取实际参数剩余…
阅读更多...
4.Isaac Jetson Nano 入门

4.Isaac Jetson Nano 入门

Isaac Jetson Nano 入门 本节介绍如何在 Jetson Nano 设备上运行 Isaac SDK 示例应用程序。 有关如何开始使用 Nano 的一般说明&#xff0c;请参阅 Jetson Nano 开发工具包入门。 文章目录Isaac Jetson Nano 入门获取 IP 地址在 Jetson Nano 上运行示例应用程序PingOpenCV 边缘…
阅读更多...
Pytorch CIFAR10图像分类 EfficientNet v1篇

Pytorch CIFAR10图像分类 EfficientNet v1篇

Pytorch CIFAR10图像分类 EfficientNet v1篇 文章目录Pytorch CIFAR10图像分类 EfficientNet v1篇4. 定义网络&#xff08;EfficientNet&#xff09;EfficientNet介绍EfficientNet性能比较EfficientNet的baselineEfficientNet模型混合缩放方法其他版本的EfficientNet(B1-B7)判断…
阅读更多...
错题 3jxn （8253复杂）

错题 3jxn （8253复杂）

A 指示型指令 C 比如 ,跟C语言的return 一样&#xff0c;可以由多条&#xff0c;但是返回的位置都是一个地方 JN NEXT RET NEXT: RET A 可以重复 EQU不可以重复 C 中断向量&#xff1a;中断服务程序的入口地址 向量中断&#xff1a;识别中断你的方法 接口 编程题&#xff…
阅读更多...
Redis关键知识点总结

Redis关键知识点总结

Reference: http://redis.cn用处缓存数据库分布式锁&#xff08;Redission的redlock&#xff0c;自定义的lock等&#xff09;过滤器&#xff08;布隆过滤器/增强的带计数的布隆过滤器/布谷鸟过滤器等&#xff09;大规模的计算辅助&#xff08;bitmap&#xff09;消息订阅/监听 …
阅读更多...
PyQt5入门学习（一）【小白入门系列】

PyQt5入门学习（一）【小白入门系列】

PyQt5入门学习 介绍&#xff1a;PyQt5是Python较好的图形库&#xff0c;与C的Qt不同的是PyQt5封装得较为简单&#xff0c;上手也更加的方便。下面话不多说&#xff0c;开始学习PyQt5吧&#xff01; 安装过程 安装方法有两种&#xff0c;一种是下载PyQt5最新源码进行编译安装…
阅读更多...
初识Kafka

初识Kafka

1.1 定义 Kafka传统定义: Kafka是一个分布式的基于发布/订阅模式的消息队列(MessageQueue&#xff09;&#xff0c;主要应用于大数据实时处理领域。 发布/订阅: 消息的发布者不会将消息直接发送给特定的订阅者&#xff0c;而是将发布的消息分为不同的类别&#xff0c;订阅者只…
阅读更多...
[数据结构基础]二叉树——堆的概念、结构、接口函数及经典的Topk问题和堆排序问题

[数据结构基础]二叉树——堆的概念、结构、接口函数及经典的Topk问题和堆排序问题

目录 一. 堆的概念及结构 1.1 堆的概念 1.2 堆的结构及在内存中的存储 二. 堆的主要接口函数 2.1 堆初始化函数HeapInit 2.2 堆销毁函数HeapDestroy 2.3 向堆中插入数据函数HeapPush&#xff08;以小堆为例&#xff09; 2.4 删除堆根节点数据函数HeapPop&#xff08;小…
阅读更多...
C++ 夺冠！成为 TIOBE 2022 年度编程语言

C++ 夺冠！成为 TIOBE 2022 年度编程语言

目录&#xff1a;C夺冠—成为TIOBE2022年度编程语言一、前言二、C 摘得桂冠三、Top 10 编程语言 TIOBE 指数走势&#xff08;2002-2023&#xff09;四、历史排名&#xff08;1987-2023&#xff09;五、编程语言“名人榜”&#xff08;2003-2022&#xff09;六、说明一、前言 2…
阅读更多...
vitepress（三）：自动生成目录

vitepress（三）：自动生成目录

上一节我们将自己的网站发布到了git pages上&#xff0c;但是现在我们需要每次更新一篇文章就重写一次目录&#xff0c;操作上十分的繁琐和不方便&#xff0c;所以我们需要一个方法去自动生成我们的侧边栏结构&#xff0c;方便我们每次只需要更新我们的项目即可。这里我们要知道…
阅读更多...
【每日一题】【LeetCode】【第六天】【Python实现】加一

【每日一题】【LeetCode】【第六天】【Python实现】加一

加一的解决之路 题目描述 测试案例&#xff08;部分&#xff09; 第一次 1这个很好理解&#xff0c;唯一的难点就是个位1导致的进位的问题&#xff0c;可能会只会导致十位1&#xff0c;也有像8999这样产生多次进位的情况。 为了解决进位问题&#xff0c;自己想到了第三天学…
阅读更多...
mysql三表查询15个例子带你搞懂它

mysql三表查询15个例子带你搞懂它

mysql三表查询30个经典案例创建三个表a、b、c表a中的数据表b中的数据表c中的数据1.查询出学习成绩70分以上的学生姓名与成绩与学科&#xff1b;2.查询姓名以mi结尾的学生姓名及其任课老师姓名&#xff1b;3.选修课名为math的学生学号与姓名;4.选修课号为C4的学生学号&#xff1…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023