几何图形组成了世界万物，在数学史具有重要地位，将几何图形迁移到地理空间信息的处理上，我们我们得到就是研究区域的边界范围，因此，在学习矢量数据和栅格数据之前，我们有必要了解几何图形在GEE上的编辑。
1.直接绘制图形
在GEE内置的地图上，提供了地图绘制的工具，界面如下：
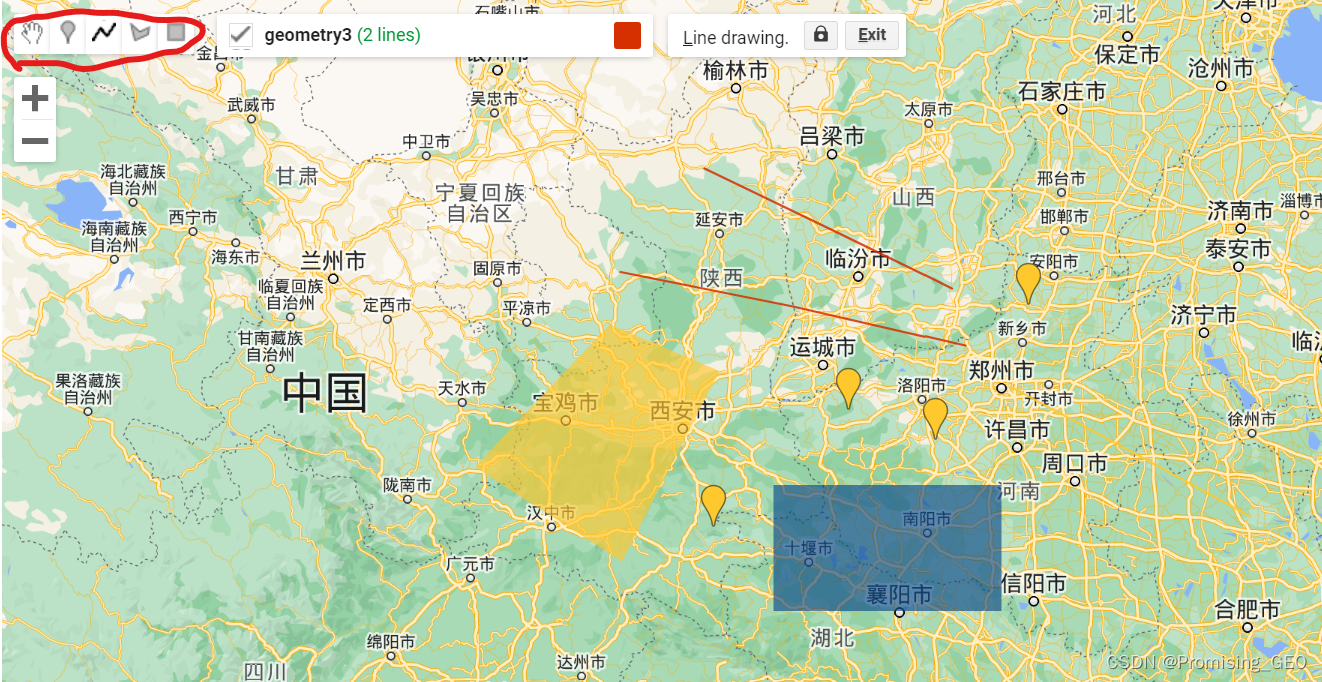
在地图编辑窗口中有点、线、任意形状、矩形形状的绘制工具，用户可以根据自己想绘制的图形类型，选中相应的工具进行图形的绘制即可。此处小编随意绘制点、线、面等图形，大家可以动动小手自己尝试一下。
2.代码定义几何图形
如果你拥有点位坐标，想要精确绘制某个地方的几何图形，可以采用代码编辑栏，进行如下的代码编辑：
（1）定义点
//定义一个点
var point1 = ee.Geometry.Point([114.9054831122441,25.85194534606585]);
var point2 = ee.Geometry.Point([115.07989107122847,26.00509220886221]);
var point3 = ee.Geometry.Point([114.79836641302535,25.95571174574036]);
//定义多个点
var point = ee.Geometry.MultiPoint([point1,point2,point3]);如果用户获取点的坐标，定义点采用:
ee.Geometry.Point([lontitude,latitude])/ee.Geometry.MultiPoint([point1,point2,pont3])
通过符号可视化后，将得到点在地图上的显示。
（2）定义线
线状地物如公路、铁路、河流等是地理数据的一大类型，GEE上可以采用如下代码进行线的定义：
//定义一条直线
var line1 = ee.Geometry.LineString([[113.15432442325019,24.673815145943788],
[110.84719551700019,26.339541619386722]]);
var line2 = ee.Geometry.LineString([[114.31887520450019,27.04624966596319],
[114.42873848575019,24.57394257050962]]);
print("line1",line1,"line2",line2);
//定义多条直线
var line = ee.Geometry.MultiLineString([line1,line2]);
print("line",line);使用：
ee.Geometry.LineString([point1,point2,point3])/ee.Geometry.MultiLineString([line1,line2])
实现对一条线或多条线的定义。
（3）定义面
面状地物的定义与点和线的定义类似，具体如下：
//定义一个几何面
var polygon1 = ee.Geometry.Polygon([[[109.41897286075019,27.534421917013297],
[107.46340645450019,26.319848479663218],
[110.42971504825019,26.673810932870065],
[109.41897286075019,27.534421917013297]]]);
var polygon2 = ee.Geometry.Polygon([[[107.26565254825019,24.77360781003692],
[106.29885567325019,24.97295245118669],
[106.89211739200019,23.61114760624955],
[108.58401192325019,24.81350244702575],
[108.18850411075019,25.74729788986625],
[106.69436348575019,25.72750505868025],
[107.26565254825019,24.77360781003692]]]);
print("polygon1",polygon1,"polygon2",polygon2);
//定义多个几何面
var polygon = ee.Geometry.MultiPolygon([polygon1,polygon2]);
print("polygon",polygon);使用：
ee.Geometry.Polygon([[[.........]]])/ee.Geometry.MultiPolygon([polygon1,polygon2])
完成对面或者是多个面的定义。
（4）定义矩形
如果想要规则定义研究区域范围，GEE也提供了定义矩形的代码方法：
// 定义矩形的左上角和右下角坐标
var topLeft = ee.Geometry.Point(-74.05, 40.7);
var bottomRight = ee.Geometry.Point(-73.95, 40.6);
// 使用左上角和右下角坐标创建矩形
var rectangle = ee.Geometry.Rectangle(topLeft, bottomRight);使用如下格式定义一个矩形范围：
ee.Geometry.Rectangle(左上角坐标，右上角坐标)
3.形状的操作方法
（1）定义案例研究区域
//定义不同的几何图形
var polygon1 = ee.Geometry.Polygon([[[116.0466463153445,28.8833257353102],
[116.8156892840945,29.859865982108825],
[115.2336580340945,30.069258158106802],
[116.0466463153445,28.8833257353102]]]);
var polygon2 = ee.Geometry.Polygon([[[114.8930818622195,28.439880647311266],
[117.2551424090945,28.439880647311266],
[117.2551424090945,29.61183506255461],
[114.8930818622195,29.61183506255461],
[114.8930818622195,28.439880647311266]]]);
Map.centerObject(polygon1,6);
Map.addLayer(polygon1,{"color":"red"},"polygon1");
Map.addLayer(polygon2,{"color":"blue"},"polygon2");（2）求面积，外接矩形，形状中心点，打印坐标
//求几何图形的面积
print("Area:",polygon1.area());
//求几何图形的边界矩形
print("Bounds:",polygon1.bounds());
//求几何图形的中心点
print("centroid:",polygon1.centroid());
//求几何中心的坐标
print("Coordinate:",polygon1.coordinates());得到的结果如下：
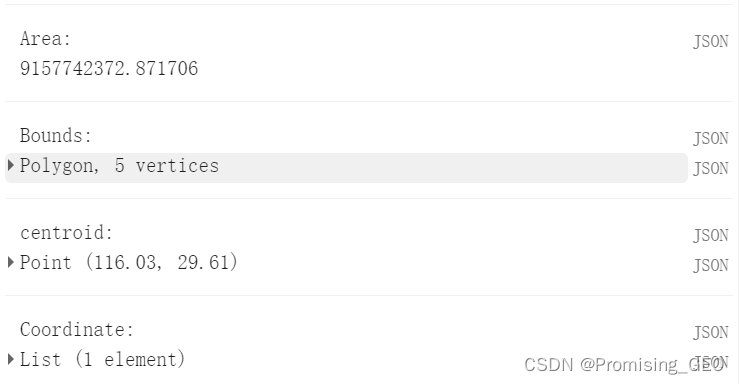
（3）判断形状相交与求交集形状
//求几何图形的交集
print("Is intersect?",polygon1.intersects(polygon2));
var intersection = polygon1.intersection(polygon2);
Map.addLayer(intersection,{},"intersection");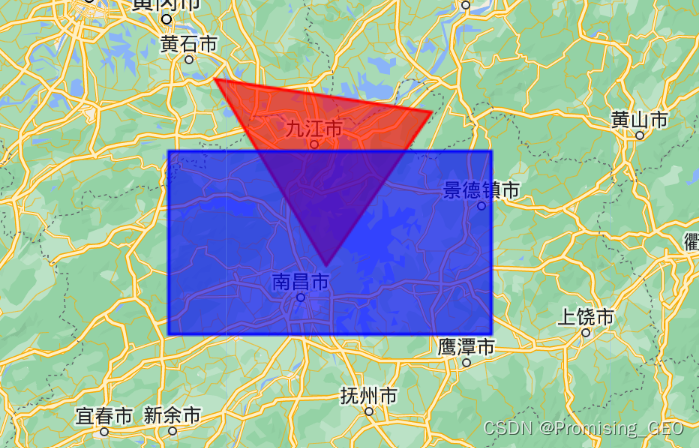
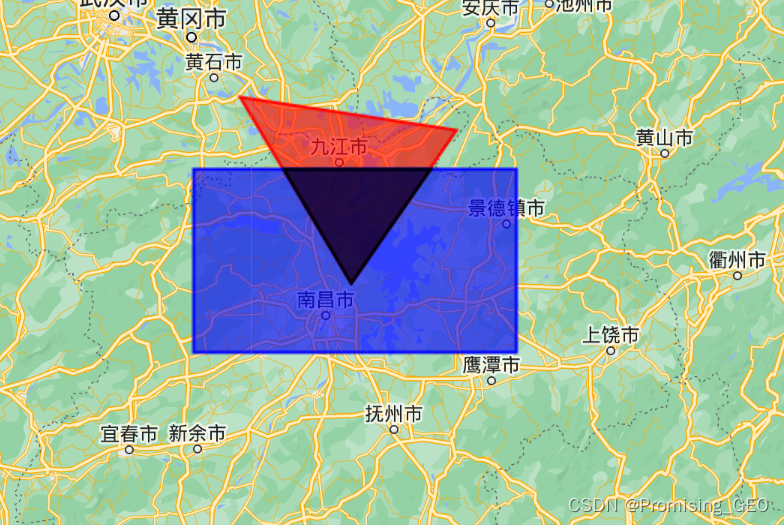
注意intersects和intersection的区别，前者返回逻辑运算符，后者返回形状结果。
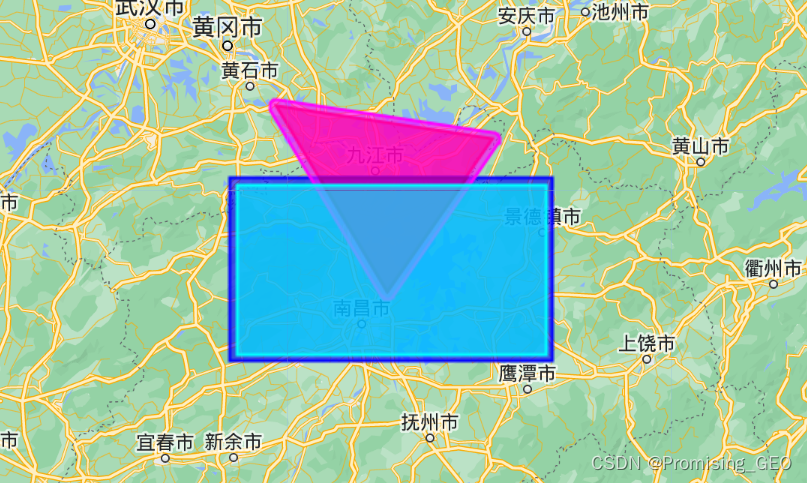
（4）缓冲区的生成
//生成2000m外缓冲区
var bufferpolygon1 = polygon1.buffer(2000);
Map.addLayer(bufferpolygon1,{"color":"ff00ff"},"buffePolygon1");
//生成2000m内缓冲区
var bufferpolygon2 = polygon2.buffer(-2000);
Map.addLayer(bufferpolygon2,{"color":"00ffff"},"bufferPolygon2");
//缓冲区裁剪
var differ = bufferpolygon1.difference(bufferpolygon2);
Map.addLayer(differ,{"color":"green"},"differ");缓冲区包括外缓冲区（正号）和内缓冲区（负号），以及缓冲区的相交部分，运行结果如下：
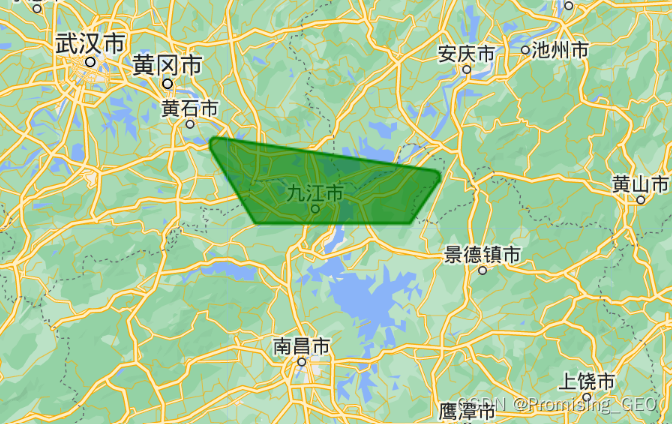
关于GEE的几何图形的相关操作分享到这里，希望对大家学习GEE有帮助。如果对你的学习有帮助，别忘记了给小编点赞哦！
案例代码链接：
https://code.earthengine.google.com/2a23cd62643bd8ad86d31f100313d240
https://code.earthengine.google.com/2a23cd62643bd8ad86d31f100313d240GEE学习之路不易，祝大家新学期更上一层楼！
