0 FQA:

Q1，什么是Mean Teacher？ MT的训练方式是怎样的？
A1: Mean Teacher是一种基于一致性正则化的半监督学习框架，从Π-model与时序集成演化而来。该模型由一个教师模型和一个学生模型组成，两者使用相同的网络结构。在训练过程中，该方法对学生和教师模型添加不同的扰动，并通过最小化二者的输出差异训练模型，使模型在不同扰动下的输出结果仍具有一致性，从而有效提升模型的泛化能力。

Q2:为什么叫平均教师?
A2： 因为在MT模型的训练过程中，Mean Teacher 首先对学生模型进行训练，并利用梯度下降法更新其模型参数，其次计算学生模型参数的指数移动平均值，并将计算结果更新为教师模型的参数。由于教师模型是连续若干训练step产生的学生模型的平均值，我们称之为平均教师方法。

Q3: MT与时序集成的不同点在哪？
A3: 与 Temporal Ensembling 方法的不同之处在于，Mean Teacher 并未对模型的输出结果进行操作，而是关注于对模型参数的处理。

Q4：后续的引用MT的文章中，都有那些创新思路？ 比如说对着Mean Teacher结构上是如何创新点等等？
A4：感觉mean teacher 的变化形式特别的多，我先对着mean teacher为主题进行调研，再来回答这个问题。

1 Mean Teacher

Mean Teacher 论文名 Mean teachers are better role models: Weight-averaged consistency targets improve semi-supervised deep learning results
论文地址链接：https://arxiv.org/pdf/1703.01780.pdf

1.1 Mean Teacher简介

Mean Teacher 是一种半监督学习方法，是在方法 Π-Model 和 Temporal Ensembling 之上做了一些改进。 Π
-Model 和 Temporal Ensembling 方法都是用了单个模型，而 Mean Teacher 是用了两个模型。 Teacher 的学习方法是参数进行动量更新。Student 则是普通的学习方式。

1.2 回顾Π-Model 和 Temporal Ensembling

• Π-Model 对一个 Batch 的数据做两次不同数据增强（例如两次不同的噪声），然后把两次不同数据增强后结果分别输入到同一个模型中，最终的损失函数对于有类标的样本是一个数据增强和类标的交叉熵，另一个是两个数据增强输出的最小二乘损失，对于无类标样本是两个数据增强输出的最小二乘损失。
• Temporal Ensembling 和 Π-Model 基本上是一样的，区别在于一个样本在一个epoch中只需要进行一次数据增强即可。原始的模型计算两个损失项以充分利用无标签数据，第一项是带标签数据输入模型后的预测值与标签的交叉熵损失，第二项是对无标签数据施加两种不同的干扰（数据增强），理论上施加数据扰动后的属性值应该不变，这时候就使用均方差损失函数计算两个预测值之间的“距离”。这种思想其实是自监督学习的思想，然后被移植到半监督学习领域了。但是，每一次的计算都需要进行多次的前向传播，显然这会很耗费时间，而且随着数据的变动，模型参数更新的方向也会增加不确定性。为此，引入了集成模型的思想，而且是时序集成，即将Π模型的zi 视为过去若干step预测值的集成，而非单一模型的预测值。这样能够充分利用模型学习的过往经验，使得整个预测过程更具有鲁棒性。集成模型的思想很常见，如Adaboost, dropout等。很显然，这是一个以空间换时间的策略，因为要开辟一定的内存空间存放历史的预测值，但是对缩短训练时间的贡献是卓越的。

Q： Because the targets change only once per epoch, Temporal Ensembling becomes unwieldy when learning large datasets. 怎么理解？
_A：_应该是代表zi 要等一个epoch遍历后才能得到更新，实际上无标签数据的预测属性值是和很久远的平均状态进行对比，而不是跟当前步最新的平均状态进行对比。在面对大型数据集时会显得“迟钝”。

1.3 Mean Teacher

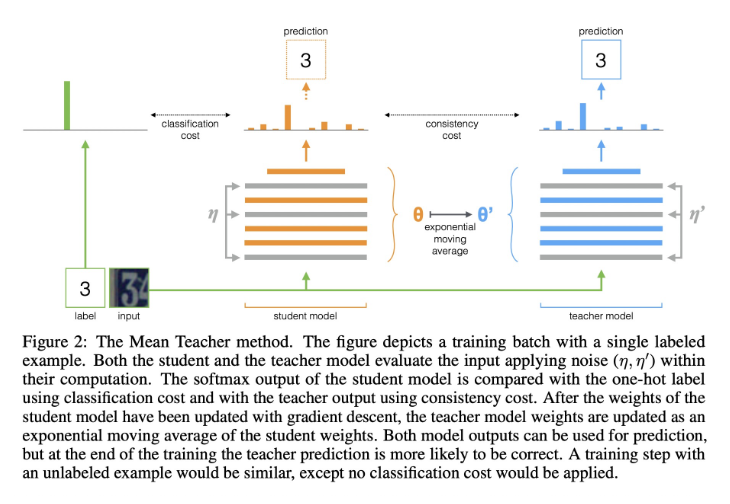
在 Mean Teacher 这篇论文中，加入了知识蒸馏中 Teacher 和 Student 的概念来解释其方法。这里面的 Student 表示直接和正确类标计算交叉熵的一组数据增强输入，另外一组只计算最小二乘损失的数据增强输入为 Teacher（因为 Teacher 不再从原始输入中学习了嘛）。

为了克服时序集成（Temporal Ensembling）的局限性，我们采用平均模型权重而不是平均模型预测的方法。
由于教师模型是连续若干训练step产生的学生模型的平均值，我们称之为平均教师方法。平均模型权重往往会产生一个比直接使用最终权重更精确的模型。教师模型使用学生模型的EMA权重，而不是与学生模型共享权重。
现在它可以在每一个step完成后即刻聚合之前学习到的所有信息，而不仅仅在每一个epoch。此外，由于EMA提高了所有层的输出质量，而不仅仅是最后一层的输出，因此模型能够更好地表征中层乃至高层语义信息。这些方面早就了该模型相对于Temporal ensemble的两个优势。
首先，更准确的标签使学生和教师模型之间发生更快的反馈循环，从而产生更好的精度。其次，这种方法适用于大型数据集和在线学习。

形式化描述，Student 和 Teacher 的损失函数为：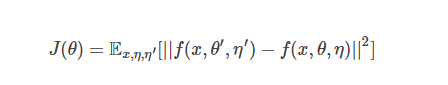

其中 θ和θ’分别是 Student 和 Teacher 的模型参数，η和η’分别是 Student 和 Teacher 的噪声扰动，Teacher 模型参数的更新方法是: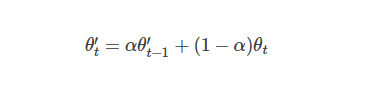

参考：
【论文阅读笔记：Mean teachers are better role models】
https://zhuanlan.zhihu.com/p/467917019
【Mean teacher 论文阅读】
https://zhuanlan.zhihu.com/p/526985640