pythonJax小记（五）：python: 使用Jax深度图像（正交投影和透视投影之间的转换）（持续更新，评论区可以补充）

python: 使用Jax深度图像（正交投影和透视投影之间的转换）

前言
问题描述
- 1. 透视投影
- 2. 正交投影
直接上代码
解释
- 1. `compute_projection_parameters` 函数
- - a. 参数解释
  - b. 函数计算
- 2. `ortho_to_persp` 函数
- - a. 计算投影参数：
  - b. 生成像素坐标网格：
  - c. 计算透视深度值：
- 3. `persp_to_ortho` 函数
- - a. 计算投影参数：
  - b. 生成像素坐标网格：
  - c. 计算正交深度值：

前言

自用，刚开始接触可能顺序会比较乱。

问题描述

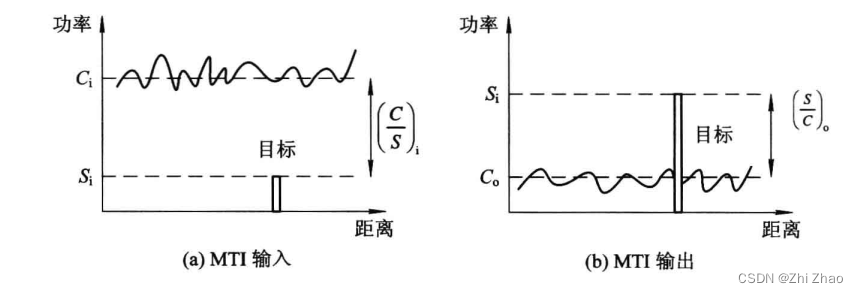
目前我知道的（欢迎评论区补充）照相机生成的深度图像有两种方法（如下图）：
在这里插入图片描述

在透视投影中，物体的大小和形状会根据其距离观察者的远近而发生变化，这是因为透视投影模拟了人眼或相机镜头观察世界的方式，远处的物体看起来更小，近处的物体看起来更大。而在正交投影中，物体的大小和形状与其距离无关，提供了一种更抽象但尺寸精确的视图。

现在假设照相机正在观察一个又大平面又平整的物体:

1. 透视投影

在透视投影中，物体的大小会随着距离相机的远近而变化，即距离相机越远，物体在图像上看起来越小。这种投影方式能够模拟人眼观察世界的方式，因此在大多数三维图形应用中，透视投影是用来创建更加真实感的视觉效果。

在这里插入图片描述
虚线部分是照相机到照射物体的距离，从左到右依次叫做depth1p，depth2p，depth3p，depth4p，depth5p；它们之间的关系应该是:

depth1p = depth5p > depth2p = depth4p > depth3p

2. 正交投影

在正交投影中，所有的投影线都是平行的。这意味着无论物体距离相机有多远，它的大小在投影图上都保持不变。正交投影常用于工程图纸和某些类型的艺术作品，因为它不会因为透视而扭曲物体的比例。

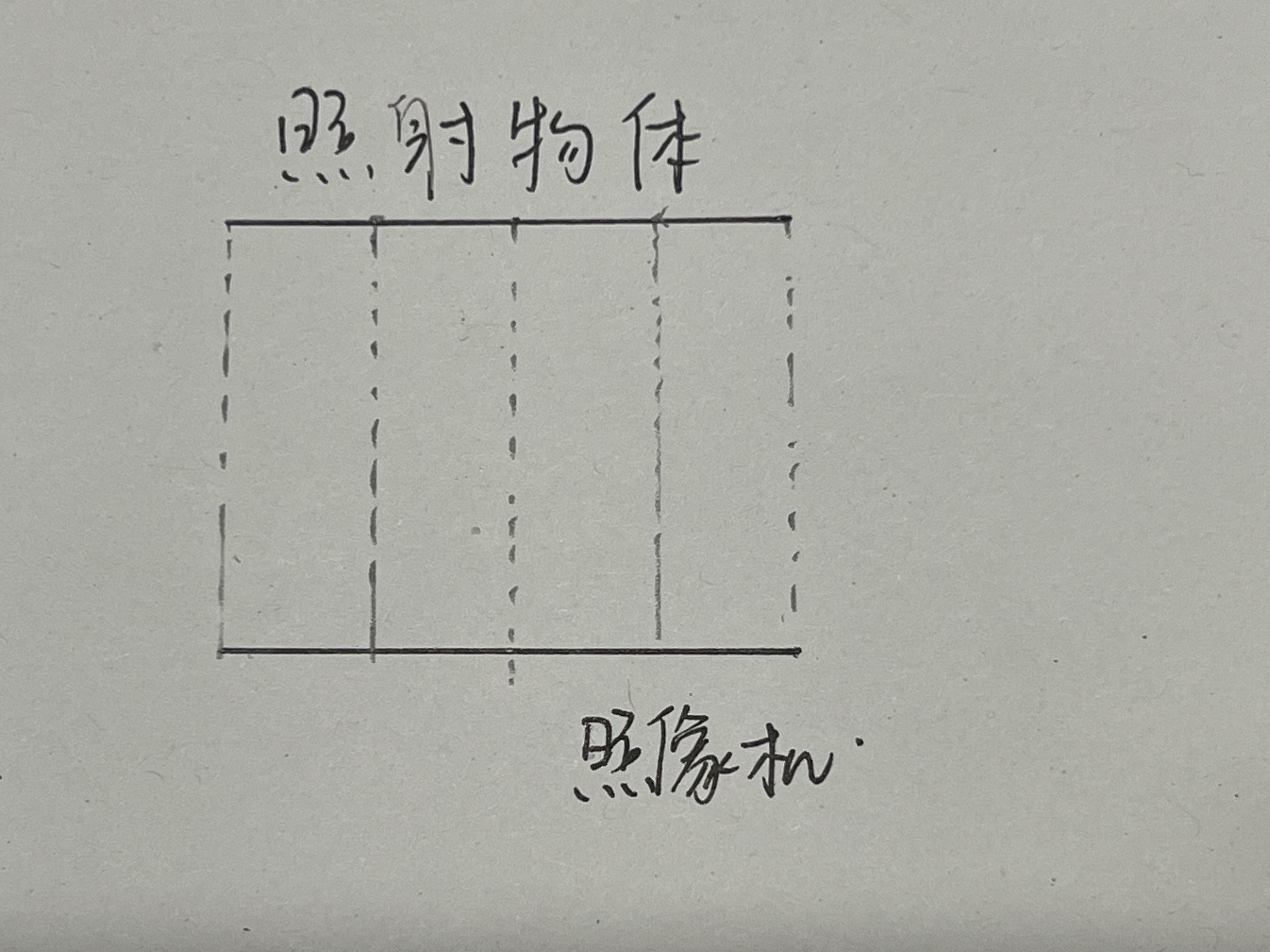
在这里插入图片描述

虚线部分是照相机到照射物体的距离，从左到右依次叫做depth1o，depth2o，depth3o，depth4o，depth5o；它们之间的关系应该是:

depth1o = depth2o = depth3o = depth4o = depth5o = depth3p(透视投影中最中心点的距离)

我想做的是depth1p <——>depth1o，depth2p <——>depth2o，depth3p <——>depth3o(数值相等不变)，depth4p <——>depth4o，depth5p <——>depth5o之间的互相转化。

直接上代码

from jax import random
import jax.numpy as jnp
from jax import jit
 
def compute_projection_parameters(fov, resolution):
    """计算透视投影所需的参数"""
    h, w = resolution
    f = 0.5 * w / jnp.tan(fov * 0.5)  # 假设fov是水平的
    # f = 0.5 * h / jnp.tan(fov * 0.5)  # 假设fov是竖直的
    cx, cy = w * 0.5, h * 0.5
    return f, cx, cy
 
@jit
def ortho_to_persp(depth_ortho, fov, resolution):
    """正交投影深度图转换为透视投影深度图"""
    f, cx, cy = compute_projection_parameters(fov, resolution)
    y, x = jnp.indices(depth_ortho.shape)
    z = depth_ortho
    x_persp = (x - cx) * z / f
    y_persp = (y - cy) * z / f
    depth_persp = jnp.sqrt(x_persp**2 + y_persp**2 + z**2)
    return depth_persp
 
@jit
def persp_to_ortho(depth_persp, fov, resolution):     
    """透视投影深度图转换为正交投影深度图"""    
    f, cx, cy = compute_projection_parameters(fov, resolution)     
    y, x = jnp.indices(depth_persp.shape)     
    # 逆向透视效果调整深度值    
    z = depth_persp     
    # 假设所有点在深度图中直接面向相机，计算透视图中的实际深度    
    depth_ortho = z / jnp.sqrt(((x - cx) / f)**2 + ((y - cy) / f)**2 + 1)     
    return depth_ortho
 
# 创建随机键
key = random.PRNGKey(0)
 
# 示例参数
fov = jnp.radians(58.0)  # 58度的视场
resolution = (555, 555)  # 深度图的分辨率
 
# 使用JAX的随机数生成函数来创建假设的深度图
depth_ortho = random.uniform(key, resolution)
depth_persp = random.uniform(key, resolution)
 
# 执行转换
depth_persp_converted = ortho_to_persp(depth_ortho, fov, resolution)
depth_ortho_converted = persp_to_ortho(depth_persp, fov, resolution)
 
print("depth_ortho[277][277]:")
print(depth_ortho[277][277])
print("depth_ortho:")
print(depth_ortho)
print("depth_persp_converted[277][277]:")
print(depth_persp_converted[277][277])
print("depth_persp_converted:")
print(depth_persp_converted)
 
print("depth_persp[277][277]:")
print(depth_persp[277][277])
print("depth_persp:")
print(depth_persp)
print("depth_ortho_converted[277][277]:")
print(depth_ortho_converted[277][277])
print("depth_ortho_converted:")
print(depth_ortho_converted)

输出：

depth_ortho[277][277]:
0.17295325
depth_ortho:
[[0.63084936 0.12969959 0.13633609 ... 0.5946181  0.59479845 0.4128834 ]
[0.29537833 0.3383578  0.5370909  ... 0.53237784 0.90082276 0.5761422 ]
[0.32716596 0.12419498 0.6801119  ... 0.55152595 0.48904026 0.8486302 ]
...
[0.30268252 0.2692206  0.73559785 ... 0.210132   0.06937218 0.61453307]
[0.30586207 0.18751395 0.5052029  ... 0.364128   0.3952657  0.09071398]
[0.64812434 0.6937938  0.5302503  ... 0.21545482 0.274127   0.7742363 ]]
depth_persp_converted[277][277]:
0.17295341
depth_persp_converted:
[[0.8015802  0.16468817 0.17299668 ... 0.7539958  0.75473905 0.5242654 ]
[0.37506145 0.4293407  0.68104595 ... 0.6746088  1.142268   0.73106426]
[0.41514048 0.15748264 0.8618096  ... 0.6983931  0.61969155 1.0760863 ]
...
[0.38381162 0.34114605 0.93148196 ... 0.26590642 0.08784546 0.7787128 ]
[0.388108   0.23777282 0.6401722  ... 0.46109253 0.5008643  0.11502781]
[0.82296646 0.88035184 0.6723719  ... 0.2730161  0.34760055 0.98242503]]
depth_persp[277][277]:
0.17295325
depth_persp:
[[0.63084936 0.12969959 0.13633609 ... 0.5946181  0.59479845 0.4128834 ]
[0.29537833 0.3383578  0.5370909  ... 0.53237784 0.90082276 0.5761422 ]
[0.32716596 0.12419498 0.6801119  ... 0.55152595 0.48904026 0.8486302 ]
...
[0.30268252 0.2692206  0.73559785 ... 0.210132   0.06937218 0.61453307]
[0.30586207 0.18751395 0.5052029  ... 0.364128   0.3952657  0.09071398]
[0.64812434 0.6937938  0.5302503  ... 0.21545482 0.274127   0.7742363 ]]
depth_ortho_converted[277][277]:
0.17295307
depth_ortho_converted:
[[0.49648297 0.10214445 0.10744441 ... 0.46892923 0.4687517  0.32516485]
[0.23262416 0.26665536 0.4235641  ... 0.42013407 0.7104127  0.45405012]
[0.25783455 0.09794345 0.53672194 ... 0.4355439  0.3859345  0.6692523 ]
...
[0.23870227 0.21245952 0.58090675 ... 0.1660564  0.05478369 0.4849681 ]
[0.24104528 0.14787847 0.39868954 ... 0.2875544  0.31193072 0.07153945]
[0.510428   0.5467698  0.41816944 ... 0.17002945 0.21618383 0.6101655 ]]

解释

1. `compute_projection_parameters` 函数

compute_projection_parameters函数的目的是根据给定的视场角（Field of View, FOV）和图像分辨率来计算透视投影所需的参数。这些参数主要是焦距（f）和图像的中心点坐标（cx,cy）。这些参数对于将三维空间中的点投影到二维图像平面上，以及进行透视投影与正交投影之间的转换非常重要。

a. 参数解释

fov：视场角，表示相机视角的宽度。在三维图形和计算机视觉中，FOV是一个关键参数，因为它定义了可见场景的范围。视场角越大，相机能够看到的场景就越宽广。
resolution：图像分辨率，通常以像素为单位表示图像的宽度和高度。在这个上下文中，分辨率告诉我们图像平面的尺寸，这对于计算图像中点的位置非常重要。

b. 函数计算

焦距（f） 的计算基于视场角（FOV）和图像宽度。焦距是一个表示相机与图像平面之间距离的参数，它影响着场景在图像平面上的投影方式。在这个函数中，焦距是通过下面的公式计算的：
$f = 0.5 \times w i d t h / t an (FO V /2)$
这个公式利用了简单的三角形几何关系，其中假设图像平面的宽度直接对应于视场角的跨度。通过这个公式，我们可以根据视场角和图像宽度计算出焦距。

图像中心点坐标（cx,cy） 的计算很直接：它们是图像宽度和高度的一半。图像中心点是图像平面上的一个关键参考点，因为它通常被用作投影和反投影过程中的原点。

2. `ortho_to_persp` 函数

ortho_to_persp函数的目的是将正交投影的深度图转换为透视投影的深度图。这个转换过程需要根据视场角（FOV）、图像分辨率以及焦距（f）和图像中心（cx, cy）这些计算出的投影参数来完成。

a. 计算投影参数：

首先，利用compute_projection_parameters函数根据FOV和图像分辨率计算出焦距（f）和图像中心（cx, cy）。

b. 生成像素坐标网格：

使用jnp.indices生成一个与输入深度图相同尺寸的像素坐标网格。这个网格包含了每个像素点的行（y）和列（x）坐标。

c. 计算透视深度值：

通过(x - cx)和(y - cy)计算每个像素点相对于图像中心的偏移。
使用偏移值和深度值（z）以及焦距（f）来调整每个像素的深度值。这里，深度值（z）乘以偏移量除以焦距，计算出在透视视图下像素的“新”位置。
最后，利用jnp.sqrt(x_persp**2 + y_persp**2 + z**2)计算每个像素点在透视投影中的实际深度值。这个步骤通过考虑像素在透视投影中的三维空间位置（考虑深度z）来调整深度图，使得远处的物体看起来更小，近处的物体看起来更大。

3. `persp_to_ortho` 函数

persp_to_ortho函数的目的是将透视投影的深度图转换为正交投影的深度图。这个过程需要逆转透视投影中深度与像素位置关系的影响，恢复到一个正交视图中，其中物体的大小不会因为它们距离相机的远近而改变。

a. 计算投影参数：

首先，利用compute_projection_parameters函数根据FOV和图像分辨率计算出焦距（f）和图像中心（cx, cy）。

b. 生成像素坐标网格：

使用jnp.indices生成一个与输入深度图相同尺寸的像素坐标网格。这个网格包含了每个像素点的行（y）和列（x）坐标。

c. 计算正交深度值：

在公式depth_ortho = z / jnp.sqrt(((x - cx) / f)**2 + ((y - cy) / f)**2 + 1)中：

(x - cx)和(y - cy)计算的是像素点相对于图像中心的位置差异。
/ f是根据焦距来缩放这些差异，使其与实际的视角对应起来。
((x - cx) / f)**2 + ((y - cy) / f)**2计算的是像素点从图像中心到该点的距离的平方，这个距离是在图像平面上的。
+1实际上是在计算直角三角形的斜边长度时必须添加的项。想象一个直角三角形，其中(x - cx) / f和(y - cy) / f代表两个直角边上的长度，而我们想要找的是斜边的长度，即从相机到像素点的实际距离。在这种情况下，+1代表了这个直角三角形斜边计算中的垂直边（即相机到图像平面的距离），它是一个常数，因为在透视投影中，所有的像素点都是从相同的焦点投影到图像平面上的。+1在这里同时确保了对于所有像素，即使在图像中心（x=cx,y=cy）也能正确处理深度值。
最后用已知的深度z比上这个比例得到正交投影下的深度值。