🚀点击这里跳转到本专栏，可查阅专栏顶置最新的指南宝典~

🎉🎊🎉 你的技术旅程将在这里启航！
从基础到实践，深入学习。无论你是初学者还是经验丰富的老手，对于本专栏案例和项目实践都有参考学习意义。
✨✨✨ 每一个案例都附带关键代码，详细讲解供大家学习，希望可以帮到大家。正在不断更新中~

一.基于卷积神经网络的艺术品瑕疵检测与修复

随着人工智能技术的不断发展，其在各个领域的应用也日益广泛。本文将重点关注人工智能在文化遗产保护领域中的应用，具体探讨基于卷积神经网络（CNN）的艺术品瑕疵检测与修复技术。通过深度学习的方法，我们可以在保护文化艺术品的过程中更加精准地检测和修复潜在的瑕疵，为后人留下更加完整和精致的文化遗产。

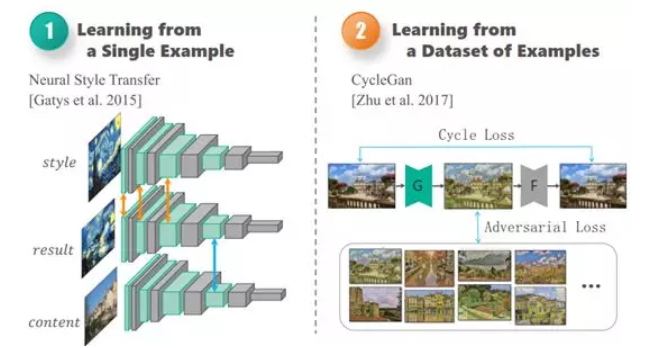
背景介绍：

文化艺术品在历史长河中扮演着重要的角色，它们不仅是人类文明的见证者，也是传承文化的载体。然而，由于时间的推移和外部环境的影响，这些艺术品常常面临着各种瑕疵和损伤。传统的修复方法往往费时费力，并且难以做到对瑕疵的精准检测与