2.1 数组运算
数组运算时MATLAB计算的基础。由于MATLAB面向对象的特性,这种数值数组称为MATLAN最重要的一种内建数据类型,而数组运算就是定义这种数据结果的方法。
2.1.1 数组的创建和操作
在MATLAB中一般使用方括号“[]”、逗号“,”、空格和分号“;”来创建数组,数组中同一行的元素使用逗号或空格进行分隔,不同行之间用分号进行分隔。
例:创建空数组、行向量、列向量示例
>> A=[]
A =
[]
>> B=[6 5 4 3 2 1]
B =
6 5 4 3 2 1
>> C=[6,5,4,3,2,1]
C =
6 5 4 3 2 1
>> D=[6;5;4;3;2;1]
D =
6
5
4
3
2
1
>> E=B'%转置
E =
6
5
4
3
2
1例:访问数组示例
>> A=[6 5 4 3 2 1]
A =
6 5 4 3 2 1
>> a1=A(1)%访问数组中的第一个元素
a1 =
6
>> a2=A(1:3)%访问数组中的第1、2、3隔元素
a2 =
6 5 4
>> a3=A(3:end)%访问数组中的第3隔到最后一个元素
a3 =
4 3 2 1
>> a4=A(end:-1:1)%数组元素反序输出
a4 =
1 2 3 4 5 6
>> a5=A([1 6])%访问数组中的第1个及第6个元素
a5 =
6 1例:子数组的赋值示例
>> A=[6 5 4 3 2 1]
A =
6 5 4 3 2 1
>> A(3)=0
A =
6 5 0 3 2 1
>> A([1 4])=[1 1]
A =
1 5 0 1 2 1在MATLAB中还可以通过其他各种方式创建数组,具体如下所示:
1.通过冒号创建一维数组
在MATLAB中,通过冒号创建一维数组的代码如下:
X=A:step:B
其中,A是创建一维数组的第一个变量,step是每次递增或递减的数值,直到最后一个元素和B的差小于或等于step的绝对值为止。
例:通过冒号创建一维数组示例
>> A=2:6
A =
2 3 4 5 6
>> B=2.1:1.5:6
B =
2.1000 3.6000 5.1000
>> C=2.1:-1:-6
C =
列 1 至 5
2.1000 1.1000 0.1000 -0.9000 -1.9000
列 6 至 9
-2.9000 -3.9000 -4.9000 -5.9000
>> D=2.1:-1.5:6
D =
空的 1×0 double 行向量2.通过logspace()函数创建一维数组
在MATLAB中常用logspace()函数创建一维数组,该函数的调用方式如下:
- y=logspace(a,b):该函数创建行向量y,第一个元素为10a,最后一个元素为10b,形成总数为50个元素的等比函数。
- y=logspace(a,b,n):该函数创建行向量y,第一个元素为10a,最后一个元素为10b,形成总是为n个元素的等比数列。
例:通过logspace()函数创建一维数组示例
>> format short
>> A=logspace(1,2,20)
A =
列 1 至 6
10.0000 11.2884 12.7427 14.3845 16.2378 18.3298
列 7 至 12
20.6914 23.3572 26.3665 29.7635 33.5982 37.9269
列 13 至 18
42.8133 48.3293 54.5559 61.5848 69.5193 78.4760
列 19 至 20
88.5867 100.0000
>> B=logspace(1,2,10)
B =
列 1 至 6
10.0000 12.9155 16.6810 21.5443 27.8256 35.9381
列 7 至 10
46.4159 59.9484 77.4264 100.00003.通过linspace()函数创建一维数组
在MATLAB中常用linspace()函数创建一维数组,该函数的调用方式:
- y=linspace(a,b):该函数创建行向量y,第一个元素为a,最后一个元素为b,形成总数为100个元素的线性间隔向量。
- y=linspace(a,b,n):该函数创建行向量y,第一个元素为a,最后一个元素为b,形成总数为n个元素的线性间隔向量。
例:通过linspace()函数创建一维数组示例
>> format short
>> A=linspace(1,100)
A =
列 1 至 11
1 2 3 4 5 6 7 8 9 10 11
列 12 至 22
12 13 14 15 16 17 18 19 20 21 22
列 23 至 33
23 24 25 26 27 28 29 30 31 32 33
列 34 至 44
34 35 36 37 38 39 40 41 42 43 44
列 45 至 55
45 46 47 48 49 50 51 52 53 54 55
列 56 至 66
56 57 58 59 60 61 62 63 64 65 66
列 67 至 77
67 68 69 70 71 72 73 74 75 76 77
列 78 至 88
78 79 80 81 82 83 84 85 86 87 88
列 89 至 99
89 90 91 92 93 94 95 96 97 98 99
列 100
100
>> B=linspace(1,36,12)
B =
列 1 至 6
1.0000 4.1818 7.3636 10.5455 13.7273 16.9091
列 7 至 12
20.0909 23.2727 26.4545 29.6364 32.8182 36.0000
>> C=linspace(1,36,1)
C =
362.1.2数组的常见运算
1.数组的算术运算
数组的运算是从数组的单个元素出发,针对每个元素进行的运算。在MATLAB中,一维数组的算术运算包括加、减、乘、左除、右除和乘方。
数组的加减运算:通过格式A+B或A-B可实现数组的加减运算。但是运算规则要求数组A和B的维数相同。
提示:如果两个数组的维数不相同,则将给出错误的信息。
例:数组的加减运算
>> clear all
>> A=[1 5 6 8 9 6]
A =
1 5 6 8 9 6
>> B=[9 85 6 2 4 0]
B =
9 85 6 2 4 0
>> C=[1 1 1 1 1]
C =
1 1 1 1 1
>> D=A+B%加法
D =
10 90 12 10 13 6
>> E=A-B%减法
E =
-8 -80 0 6 5 6
>> F=A*2
F =
2 10 12 16 18 12
>> G=A+3%数组与常数的加法
G =
4 8 9 11 12 9
>> H=A-C对于此运算,数组的大小不兼容。
数组的乘除运算:通过格式“.*“或”./”可实现数组的乘除运算。但是运算规则要求数组A和B的维数相同。
乘法:数组A和B的维数相同,运算为数组对应元素相乘,计算结果与A和B是相同维数的数组。
除法:数组A和B的维数相同,运算为数组对应元素相除,计算结果与A与B是相同维数的数组。
右除和左除的关系:A./B=B.\A,其中A是被除数,B是除数。
提示:如果两个数组的维数不相同,则将给出错误的信息。
例:数组的乘法运算示例
>> clear all
>> A=[1 5 6 8 9 6]
A =
1 5 6 8 9 6
>> B=[9 5 6 2 4 0]
B =
9 5 6 2 4 0
>> C=A.*B%数组的点乘
C =
9 25 36 16 36 0
>> D=A*3%数组与常数的乘法
D =
3 15 18 24 27 18例:数组的除法运算示例
>> A=[1 5 6 8 9 6]
A =
1 5 6 8 9 6
>> B=[9 5 6 2 4 0]
B =
9 5 6 2 4 0
>> C=A.\B%数组和数组的左除
C =
9.0000 1.0000 1.0000 0.2500 0.4444 0
>> D=A./B%数组和数组的右除
D =
0.1111 1.0000 1.0000 4.0000 2.2500 Inf
>> E=A./3%数组与常数的除法
E =
0.3333 1.6667 2.0000 2.6667 3.0000 2.0000
>> F=A/3
F =
0.3333 1.6667 2.0000 2.6667 3.0000 2.0000通过乘方格式“.^”实现数组的乘方运算。数组的乘方运算包括数组间的乘方运算、数组与某个具体数值的乘方运算,以及常数与数组的乘方运算。
例:数组的乘方运算示例
>> A=[1 5 6 8 9 6]
A =
1 5 6 8 9 6
>> B=[9 5 6 2 4 0]
B =
9 5 6 2 4 0
>> C=A.^B%数组的乘方
C =
列 1 至 5
1 3125 46656 64 6561
列 6
1
>> D=A.^3%数组与某个数值的乘方
D =
1 125 216 512 729 216
>> E=3.^A%常数与数组的乘方
E =
列 1 至 5
3 243 729 6561 19683
列 6
729通过使用函数dot()可实现数组的点积运算,但是运算要求数组A和B的维数相同,其调用格式如下:
- C=dot(A,B)。
- C=dot(A,B,dim)。
例:数组的点积运算示例
>> A=[1 5 6 8 9 6]
A =
1 5 6 8 9 6
>> B=[9 5 6 2 4 0]
B =
9 5 6 2 4 0
>> C=dot(A,B)%数组的点积
C =
122
>> D=sum(A.*B)%数组元素的乘积之和
D =
1222.数组的关系运算符
在MATLAB中提供了6中数组关系运算符,即<(小于)、<=(小于或等于)、>(大于)、>=(大于或等于)、==(恒等于)、~=(不等于)。
关系运算的运算法则如下:
- 当两个比较量是标量,直接比较两个数的大小。若关系成立,则返回的结果为1,否则为0。
- 当两个比较量是维数相等的数组时,逐一比较两个数组相同位置的元素,并给出比较结果。最终的关系运算结果是一个与参与比较的数组维数相同的数组,其组成元素为0或1。
例:数组的关系运算示例
>> A=[1 5 6 8 9 6]
A =
1 5 6 8 9 6
>> B=[9 5 6 2 4 0]
B =
9 5 6 2 4 0
>> C=A<6%数组与常数比较,小于
C =
1×6 logical 数组
1 1 0 0 0 0
>> D=A>=6%数组与常数比较,大于或等于
D =
1×6 logical 数组
0 0 1 1 1 1
>> E=A<B%数组与数组比较,小于
E =
1×6 logical 数组
1 0 0 0 0 0
>> F=A==B%数组与数组比较,恒等于
F =
1×6 logical 数组
0 1 1 0 0 03.数组的逻辑运算
在MATLAB中提供了3种数组逻辑运算符,即&(与)、|(或)和~(非)。逻辑运算的运算法则如下:
- 如果是非零元素则为真,用1表示;如果时令元素则为假,用0表示。
- 当两个比较量是维数相等的数组时,逐一比较两个数组相同位置的元素,并给出比较结果。最终的逻辑运算是一个与参与比较的数组维数相同的数组,其组成元素为0或1。
- 在进行与运算(a&b)时,a、b全为非零,则为真,运算结果为1。在进行或运算(a|b)时,只要a、b有一个为非零,则运算结果为1.在进行非运算(~a)时,若a为0,则运算结果为1;若a为非零,则元素结果为0.
例:数组的逻辑运算示例
>> A=[1 5 6 8 9 6]
A =
1 5 6 8 9 6
>> B=[9 5 6 2 4 0]
B =
9 5 6 2 4 0
>> C=A&B%与运算
C =
1×6 logical 数组
1 1 1 1 1 0
>> D=A|B%或运算
D =
1×6 logical 数组
1 1 1 1 1 1
>> E=~B%非运算
E =
1×6 logical 数组
0 0 0 0 0 12.2 矩阵操作
2.2.1创建矩阵
除了在前面提到的零矩阵、单位矩阵和全1矩阵等特殊矩阵,MATLAB中还有一些指令用于生成试验矩阵。

1.希尔伯特矩阵
希尔伯特矩阵,也称H阵,其元素为Hij=1/(i+j-1)。由于它是一个条件数差的矩阵,以将它用来作为试验矩阵。
关于希尔伯特矩阵的指令函数如下:
- bilb(n):用于生成一个n×n的希尔伯特矩阵。
- invhilb(n):用于生成一个n×n的希尔伯特矩阵的逆矩阵整数矩阵。
例:希尔伯特矩阵生成示例
>> A=hilb(3)
A =
1.0000 0.5000 0.3333
0.5000 0.3333 0.2500
0.3333 0.2500 0.2000
>> B=invhilb(3)
B =
9 -36 30
-36 192 -180
30 -180 180从结果中可以看出,希尔伯特矩阵和它的逆矩阵都是对称矩阵。
2.托普利兹矩阵
另外一个比较重要的矩阵为托普利兹矩阵,它由两个向量定义,即一个行向量和一个列向量。对称的托普利兹矩阵由单一向量来定义。
关于托普利兹矩阵的指令函数如下:
- toeplitz(k,r):用于生成非对称托普利兹矩阵,第一列为k,第一行为r,其余元素等于其左上角的元素。
- Toeplitz©:用于向量c生成一个对称托普利兹矩阵。
例:托普利兹矩阵函数示例
>> C=toeplitz(2:5,2:2:8)
C =
2 4 6 8
3 2 4 6
4 3 2 4
5 4 3 23.0~1间均匀分布的随机矩阵
在MATLAB中常用rand()函数产生0~1间均匀分布的随机矩阵,其调用格式如下:
- r=rand(n):产生维数为n×n的0~1间均匀分布的随机矩阵。
- r=rand(m,n):产生维数为n×m的0~1间均匀分布的随机矩阵。
- r=rand(m,n,p,..):产生维数为n×m×p的0~1间均匀分布的随机矩阵。
- r=rand(size(A)):产生维数为n×m×p与矩阵A相同的0~1间均匀分布的随机矩阵。
例:创建0~1间均匀分布的随机矩阵示例
>> B=rand(3)
B =
0.8147 0.9134 0.2785
0.9058 0.6324 0.5469
0.1270 0.0975 0.9575
>> C=rand([3,4])
C =
0.9649 0.9572 0.1419 0.7922
0.1576 0.4854 0.4218 0.9595
0.9706 0.8003 0.9157 0.6557
>> D=rand(size(C))
D =
0.0357 0.6787 0.3922 0.7060
0.8491 0.7577 0.6555 0.0318
0.9340 0.7431 0.1712 0.27694.标准正态分布随机矩阵
在MATLAB中常用randn()函数产生均值为0、方差为1的随机矩阵,其调用格式如下:
- r=randn(n)。
- randn(m,n)。
- r=rand(m,n,p,…)。
- r=randn([m,n,p,…])。
- r=randn(size(A))。
其格式可参考上述rand()函数。
例:创建标准正态分布随机矩阵示例
>> B=randn(3)
B =
-0.8095 0.3252 -1.7115
-2.9443 -0.7549 -0.1022
1.4384 1.3703 -0.2414
>> C=randn([3,4])
C =
0.3192 -0.0301 1.0933 0.0774
0.3129 -0.1649 1.1093 -1.2141
-0.8649 0.6277 -0.8637 -1.1135
>> D=randn(size(C))
D =
-0.0068 0.3714 -1.0891 1.1006
1.5326 -0.2256 0.0326 1.5442
-0.7697 1.1174 0.5525 0.08595.魔方矩阵
在MATLAB中常用magic()函数产生魔方矩阵。魔方矩阵中每行、每列和两条对角线上的元素和相等,其调用格式如下:
- M=magic(n)。
例:创建魔方矩阵示例
>> A=magic(3)
A =
8 1 6
3 5 7
4 9 2
>> B=magic(4)
B =
16 2 3 13
5 11 10 8
9 7 6 12
4 14 15 1
>> C=magic(5)
C =
17 24 1 8 15
23 5 7 14 16
4 6 13 20 22
10 12 19 21 3
11 18 25 2 9
>> E=sum(A)%计算每行的和
E =
15 15 15
>> F=sum(A')%计算每列的和
F =
15 15 156.帕斯卡矩阵
在MATLAB中常用pascal()函数产生帕斯卡矩阵,其调用格式如下:
- A=pascal(n):返回n阶的对称正定Pascal矩阵,其中的元素是由Pascal三角形成的。,其逆矩阵的元素都是整数。
- A=pascal(n,1):返回下三角的Cholesky因子组成的Pascal矩阵,它是对称的,所有它是自己的逆。
- A=pascal(n,2):返回pascal(n,1)的转置和交换形式。A是单位矩阵的立方和。
例:创建帕斯卡矩阵示例
>> A=pascal(4)%创建4阶帕斯卡矩阵
A =
1 1 1 1
1 2 3 4
1 3 6 10
1 4 10 20
>> B=pascal(3,2)
B =
1 1 1
-2 -1 0
1 0 07.范德蒙矩阵
在MATLAB中常用vander()函数产生范德蒙矩阵,其调用格式如下:
- A=vander(v):生成范德蒙矩阵,矩阵的列是向量v的幂,即A(I,j)=v(i)^(n-j),其中n=length(v)。
例:生成范德蒙矩阵示例
>> A=vander([1 2 3 4])
A =
1 1 1 1
8 4 2 1
27 9 3 1
64 16 4 1
>> B=vander([1;2;3;4])
B =
1 1 1 1
8 4 2 1
27 9 3 1
64 16 4 1
>> C=vander(1:.5:3)
C =
1.0000 1.0000 1.0000 1.0000 1.0000
5.0625 3.3750 2.2500 1.5000 1.0000
16.0000 8.0000 4.0000 2.0000 1.0000
39.0625 15.6250 6.2500 2.5000 1.0000
81.0000 27.0000 9.0000 3.0000 1.0000注意:使用vander()函数产生范德蒙矩阵,输入向量可以是行向量或列向量。
2.2.2改变矩阵大小
1.矩阵的合并
矩阵的合并就是把两个或者两个以上的矩阵数据连接起来得到一个新的矩阵。针对二维矩阵A、B;:
(1)[A,B]表示按列存储合并矩阵,即将B矩阵接在A矩阵的列后面;[A;B]表示按行存储合并矩阵,并将B矩阵接到A矩阵的行后面。
(2)cat(1,A,B)表示[A;B],即以行存储;cat(2,A,B)同[A,B];cat(3,A,B)表示以第3维组合A、B,组合后变成三维数组。
注意:前面姐扫的矩阵构造符[]不仅可用于构造矩阵,同时还可以作为一个矩阵合并操作符。表达式C=[A,B]在水平方向上合并矩阵A和B,而表达式C=[A;B]在竖直方向上合并矩阵A和B。
例:合并矩阵示例一
>> a=ones(3,4)
a =
1 1 1 1
1 1 1 1
1 1 1 1
>> b=zeros(3,4)
b =
0 0 0 0
0 0 0 0
0 0 0 0
>> c=[a;b]%当采用;时,上下合并拼接矩阵
c =
1 1 1 1
1 1 1 1
1 1 1 1
0 0 0 0
0 0 0 0
0 0 0 0例:合并矩阵示例二
>> a=ones(3,4);b=zeros(3,4);
>> c=[a,b]%当采用空格时,左右合并拼接矩阵
c =
1 1 1 1 0 0 0 0
1 1 1 1 0 0 0 0
1 1 1 1 0 0 0 0
>> d=[b,a]%当采用,时,左右合并拼接矩阵
d =
0 0 0 0 1 1 1 1
0 0 0 0 1 1 1 1
0 0 0 0 1 1 1 1例:合并矩阵示例三
>> a=ones(3,4);b=zeros(3,4);
>> c=cat(1,a,b)
c =
1 1 1 1
1 1 1 1
1 1 1 1
0 0 0 0
0 0 0 0
0 0 0 0
>> d=cat(2,a,b)
d =
1 1 1 1 0 0 0 0
1 1 1 1 0 0 0 0
1 1 1 1 0 0 0 0可能用矩阵合并符来构造任意大小的矩阵。不过需要注意的是,在矩阵合并的过程中一定要保证矩阵的形状是方形,否则矩阵合并将无法进行。
除了使用矩阵合并符“[]”来合并矩阵,还可以使用矩阵合并函数来合并矩阵。
2.矩阵行列的删除
要删除矩阵的某一行或某一列,只要将该行或该列赋予一个空矩阵“[]”即可。
>> A=rand(4,4)
A =
0.1386 0.2543 0.3500 0.4733
0.1493 0.8143 0.1966 0.3517
0.2575 0.2435 0.2511 0.8308
0.8407 0.9293 0.6160 0.5853
>> A(2,:)=[]
A =
0.1386 0.2543 0.3500 0.4733
0.2575 0.2435 0.2511 0.8308
0.8407 0.9293 0.6160 0.58532.2.3 重构矩阵
矩阵重构的两个比较重要的运算就是转置和共轭转置,在MATLAB中,用在函数后面加撇号”’”来表示。在线性代数的专业书籍中,这种运算经常用*和H表示。
如果A是一个实数矩阵,那么它被转置时,第一行变成第一列,第二行变成第二列……依次类推,一个m×n矩阵变成一个n×m矩阵。如果矩阵是方阵,那么这个矩阵在主队先上反映出来。如果矩阵A的元素aij是复数,那么所有元素也是共轭的。如果仅希望转置,则在撇号“’”之前输出一个点号,即成为“.’”,A.’表示转置,其结果和conj(A’)相同。如果A是实数矩阵,那么A’与A.’相同。
例:矩阵的重构示例
>> C=toeplitz(2:5,2:2:8);
>> C=C'
C =
2 3 4 5
4 2 3 4
6 4 2 3
8 6 4 22.3矩阵元素的运算
矩阵的加、减、乘、除、比较运算和逻辑运算等代数运算在MATLAB数值计算最基础的部分。
2.3.1矩阵的加减运算
进行矩阵加法、减法运算的前提时参与运算的两个矩阵或多个矩阵必须同时具有相同的行和列,即A,B,C等多个矩阵均为m×n矩阵;或者其中有一个或多个矩阵为标量。
在上述的前提下,对于同型的两个矩阵,其加法减法的定义如下:
C=A±B,矩阵C的各元素Cmn=Amn+Bmn
当其中含有标量x时:
C=A±x,矩阵C的各元素Cmn=Amn+x。
由于矩阵的加法运算归结为其元素的加法运算,容易验证,因此矩阵的加法运算满足下列的运算律:
- 交换律:A+B=B+A
- 结合律:A+(B+C)=(A+B)+C
- 存在零元:A+0=0+A=A
- 存在负元:A+(-A)+(-A)+A
例:矩阵加减法运算示例
已知矩阵A=[10 5 79 4 2;1 0 66 8 2;4 6 1 1 1],矩阵B=[9 5 3 4 2;1 0 4 -23 2;4 6 -1 1 0],行向量C=[2 1],标量x=20,试求A+B、A-B、A+B+x、A-x、A-C。
>> A=[10 5 79 4 2;1 0 66 8 2;4 6 1 1 1];B=[9 5 3 4 2;1 0 4 -23 2;4 6 -1 1 0];C=[2 1];x=20;
>> ApB=A+B
ApB =
19 10 82 8 4
2 0 70 -15 4
8 12 0 2 1
>> AmB=A-B
AmB =
1 0 76 0 0
0 0 62 31 0
0 0 2 0 1
>> ApBpX=A+B+x
ApBpX =
39 30 102 28 24
22 20 90 5 24
28 32 20 22 21
>> Amx=A-x
Amx =
-10 -15 59 -16 -18
-19 -20 46 -12 -18
-16 -14 -19 -19 -19
>> AmC=A-C对于此运算,数组的大小不兼容。
在A-C的运算中,MATLAB返回错误信息,并提示矩阵的维度必须一致。这也证明了矩阵进行加减法运算必须满足一定的前提条件。
2.3.2 矩阵的乘法运算
MATLAB中矩阵的乘法运算包括两种:数与矩阵的乘法;矩阵和矩阵的乘法。
1.数与矩阵的乘法
由于单个数在MATLAB中是以标量来存储的,因此数与矩阵的乘法也可以称为标量与矩阵的乘法。
设x为一个数,A为矩阵,则定义x与A的成绩C=Ax仍为一个矩阵,C的元素就是用数x乘矩阵A中对应的元素而得到的,即Cmnx=xAmn。数与矩阵的乘法满足下列运算律:
(1)1A=A;
(2)x(A+B)=xA+xB;
(3)(x+y)A=xA+xB;
(4)(xy)A=x(yA)=y(xA)。
例:矩阵数乘矩阵
已知矩阵A=[0 3 3;1 1 0;-1 2 3],E是三阶单位矩阵,E=[1 0 0;0 1 0;0 0 1],试求表达式2A+3E。
>> A=[0 3 3;1 1 0;-1 2 3];
>> E=eye(3);
>> R=2*A+3*E
R =
3 6 6
2 5 0
-2 4 92.矩阵和矩阵的乘法
两个矩阵的乘法必须满足被称矩阵的列数与乘矩阵的行数相等。设矩阵A为m×h矩阵,B为h×n矩阵,则两个矩阵的乘积C=A×B为一个矩阵,其Cmn=ΣHh=1=Amh×Bhn。
矩阵之间的乘法不遵循交换律,即A×B≠B×A。但矩阵乘法遵循下列运算律。
- 结合律:(A×B)×C=A×(B×C)
- 左分配律:A×(B+C)=(A×B)+(A×C)
- 右分配律:(B+C)×A=(B×A)+(C×A)
- 单位或矩阵的存在性:E×A=A,A×E=A
例:矩阵乘法示例
已知矩阵A=[2 1 4 0;1 -1 3 4],矩阵B=[1 3 1;0 -1 2;1 -3 1;4 0 -2],试求矩阵AB和BA。
>> A=[2 1 4 0;1 -1 3 4];
>> B=[1 3 1;0 -1 2;1 -3 1;4 0 -2];
>> R1=A*B
R1 =
6 -7 8
20 -5 -6
>> R2=B*A
错误使用 *用于矩阵乘法的维度不正确。请检查并确保第一个矩阵中的列数与第二个矩阵中的行数匹配。要
单独对矩阵的每个元素进行运算,请使用 TIMES (.*)执行按元素相乘。
2.3.3 矩阵的除法运算
矩阵的除法是乘法的逆运算,分为左除和右除两种,分别用运算符号“\”和“/”表示。A\B 表示矩阵A的逆乘以矩阵B,A/B表示矩阵A乘以矩阵B的逆。除非矩阵A和矩阵B相同,否则A/B和A\B是不等价的。对于一般的二维矩阵A和B,当进行A\B运算时,要求A的行数与B的行数相等;当进行A/B运算时,要求A的列数与B的列数相等。
例:矩阵的除法运算示例
设矩阵A=[1,2;1 3],矩阵B=[1 0;1 2],试求A\B和A/B。
>> A=[1,2;1 3],B=[1 0;1 2]
>> R1=A\B
R1 =
1 -4
0 2
>> R2=A/B
R2 =
0 1.0000
-0.5000 1.50002.3.4 矩阵的幂运算
当矩阵A为方阵时,可进行矩阵的幂运算,其定义为C=An=A×A×…×A(n个A),在MATLAB中,使用运算符号“^”表示幂运算。
例:方阵幂运算示例
对于给定方阵A=[2 3 8;3 1 -1;5 0 4],试求A2,A5。
>> A=[2 3 8;3 1 -1;5 0 4];
>> A2=A^3
A2 =
53 9 45
4 10 19
30 15 56
>> A5=A^5
A5 =
37496 13827 52622
10077 2887 11891
34295 11250 444642.3.5矩阵元素的查找
MATLAB中的函数find()的作用是进行矩阵元素的查找,它通常与关系函数与逻辑运算相结合,其调用格式如下:
- ind=find(X):该函数查找矩阵X中的非零元素,函数返回这些元素的单下标。
- [row,col]=find(X,…):该函数查找矩阵X中的非零元素,函数返回这些元素的双下标i,j。
例:利用函数find()查找矩阵中的元素示例
>> A=[1 3 0;3 1 0;9 2 4];
>> B=find(A);%矩阵中非零元素的下标
>> C=find(A>=1);%矩阵中大于或等于1的元素的下标
>> D=A(A>=1);%矩阵中大于或等于1的元素
>> BCD=[B,C,D]
BCD =
1 1 1
2 2 3
3 3 9
4 4 3
5 5 1
6 6 2
9 9 4
>> A(find(A==0))=10%将矩阵中等于0的元素为10
A =
1 3 10
3 1 10
9 2 42.3.6 矩阵元素的排序
MATLAB中的函数sort()的作用是按照升序排序,排序后的矩阵和原矩阵的维数相同。其调用格式如下:
- B=sort(A):该函数对矩阵A进行升序排序,A可为矩阵或向量。
- B=sort(A,dim):该函数对矩阵A进行升序排序,并将结果返回在给定的维数dim上按照升序排序。当dim=1时,按照列进行排序;当dim=2,按照行排序。
- B=sort(…,mode):该函数对矩阵A进行排序,mode可指定排序的方式。ascend指定按升序排序,为默认值,descend指定按降序排序。
例:矩阵元素的排序示例
>> A=[1 3 0;3 1 0;9 2 4];
>> B=sort(A);%矩阵中元素按照列进行排序
>> C=sort(A,2);%矩阵中元素按照行进行排序
>> D=sort(A,'descend');%矩阵中元素按照列进行降序排序
>> E=sort(A,2,'descend');%矩阵中元素按照行进行降序
>> BCDE=[B C;D E]
BCDE =
1 1 0 0 1 3
3 2 0 0 1 3
9 3 4 2 4 9
9 3 4 3 1 0
3 2 0 3 1 0
1 1 0 9 4 2例:对向量进行排序示例
>> A=[78,23,10,100,45,5,6];
>> sort(A)
ans =
5 6 10 23 45 78 1002.3.7 矩阵元素的求和
MATLAB中函数sum()和cumsum()的作用是对矩阵的元素求和。其调用格式如下:
- B=sum(A):该函数对矩阵A的元素求和,返回由矩阵A各列元素的和组成的向量。
- B=sum(A,dim):该函数返回在给定的维数dim上元素的和。当dim=1时,计算矩阵A各列元素的和;当dim=2时,计算矩阵A各行元素的和。
- B=cumsum(A)。
- B=cumsum(A,dim)。
函数cumsum()调用格式与sum()类似,不同的时其返回值为矩阵。
例:矩阵元素的求和示例
>> A=[1 3 0;3 1 0;9 2 4];
>> B=sum(A);%矩阵中元素按照列进行求和
B =
13 6 4
>> C=sum(A,2);%矩阵中元素按照行进行求和
C =
4
4
15
>> D=cumsum(A);%矩阵中各列元素的和
D =
1 3 0
4 4 0
13 6 4
>> E=cumsum(A,2);%矩阵中各行元素的和
E =
1 4 4
3 4 4
9 11 15
>> F=sum(sum(A))%矩阵中所有元素的和
F =
23提示:使用sun(sum())可求出矩阵所有元素的和。
2.3.8矩阵元素的求积
MATLAB中函数prod()和cumprod()的作用是对矩阵的元素求积。其调用格式如下:
- B=prod(A):该函数对函数A的元素求积,返回由矩阵A各列元素的积组成的向量。
- B=prod(A,dim):该函数返回在给定的维数dim上元素的积。当dim=1时,计算矩阵A各列元素的积;当dim=2,计算矩阵A各行元素的积。
- B=cumprod(A)。
- B=cumprod(A,dim)。
函数cumprod()调用个数与prod类似,不同的时其返回值为矩阵。
例:矩阵元素的求积
>> A=magic(3)
A =
8 1 6
3 5 7
4 9 2
>> B=prod(A)%矩阵各列元素的积
B =
96 45 84
>> C=prod(A,2)%矩阵各列元素的积
C =
48
105
72
>> D=cumprod(A)%矩阵各列元素的积
D =
8 1 6
24 5 42
96 45 84
>> E=cumprod(A,2)%矩阵各行元素的积
E =
8 8 48
3 15 105
4 36 722.3.9 矩阵元素的差分
MATLAB中函数diff()的作用是计算矩阵元素的差分。其调用格式如下:
- Y=diff(X):计算矩阵各列元素的差分。
- Y=diff(X,n):计算矩阵各列元素的n阶差分。
- Y=diff(X,n,dim):计算矩阵在给定的维数dim上元素的n阶差分。当dim=1时,计算矩阵各列元素的差分;当dim=2时,计算矩阵各行元素的差分。
例:计算矩阵元素的差分示例
>> A=magic(3)
A =
8 1 6
3 5 7
4 9 2
>> B=diff(A)%矩阵各列元素的差分
B =
-5 4 1
1 4 -5
>> C=diff(A,2)%矩阵各列元素的2阶差分
C =
6 0 -6
>> D=diff(A,1,1)%矩阵各列元素的差分
D =
-5 4 1
1 4 -5
>> E=diff(A,1,2)%矩阵各行元素的差分
E =
-7 5
2 2
5 -7提示:当参数n≥size(x,dim)时,函数的返回值是空矩阵。
2.4矩阵运算
矩阵运算是线性代数极其重要的部分。
2.4.1矩阵分析
MATLAB提供的矩阵分析矩阵函数如下图。

1.向量和矩阵的范数运算
对于线性空间中的一个向量x={x1,x2,…,xn},如果存在一个函数r(x)满足以下3个条件:
- r(x)>0,且r(x)=0的充要条件为x=0.
- r(ax)=|a|r(x),其中a为任意标量。
- 对向量x和y,有r(x+y)≤r(x)+r(y)
对称r(x)为向量x的范数,一般记为||x||。范数的形式多种多样,下面呢式子中定义的范数操作就满足以上3个条件:
![]() 且
且![]()
式中定义的||x||p阶范数,其中最有用的是1、2和∞阶范数。
矩阵的范数是基于向量的范数定义的,其定义式如下:
|
|
与向量的范数一样,矩阵的范数最常用的也是1、2和∞阶范数,它们的定义式如下:

在上式中,Smax{ATA}则为矩阵A的最大奇异值的平方。
在MATLAB中,求向量范数的函数的具体做法如下:
- N=norm(x,p):对任意大于1的p值,返回向量x的p阶范数。
- N=norm(x):返回向量的2阶范数,相当于N=norm(x,2)。
- N=norm(x,inf):返回向量的∞阶范数,相当于N=max(abs(x))。
- N=norm(x,-inf):返回向量的-∞阶范数,相当于N=min(abs(x))。
在MATLAB中,求矩阵范数的函数的具体用法如下:
- N=norm(A):计算矩阵的2阶范数,也就是最大奇异值。
- N=norm(A,p):根据参数p的值不同,求不同阶的范数值。当p=1时,计算矩阵A的1阶范数,相当于max(sum(abs(A)))。当p=2时,计算矩阵A的2阶范数,相当于norm(A)。当p=inf时,计算矩阵A的∞阶范数,相当于max(sum(abs(A’)))。当p=pro时,计算矩阵A的F范数,相当于sqrt(sum(diag(A’*A)))。
例:求向量x的2阶范数示例
>> norm(1:6,2)
ans =
9.5394注意:当矩阵维数比较大时,会导致计算矩阵范数的时间比较长,并且当一个近似的范数值满足要求时,可以考虑使用函数normest()来估计二阶范数值。函数normest()最初开发时是为了提供给稀疏矩阵使用的,同时它也能接收满矩阵的输入,一般在满矩阵维数比较大时使用。
函数normest()的用法如下:
- normest(S):估计矩阵S的2阶范数值。
- normest(S,tol):使用tol作为允许的相对误差。
例:求矩阵的范数示例
>> a=[1 2 3;3 4 5;7 8 9];
>> b=norm(a,1);%矩阵的1阶范数
>> c=norm(a);%矩阵的2阶矩阵
>> d=norm(a,inf);%矩阵的∞阶范数
>> e=norm(a,'fro');%矩阵的Frobenius范数
>> f=normest(a);%矩阵的2阶范数的估计值
>> bcdef=[b c d e f]
bcdef =
17.0000 16.0216 24.0000 16.0624 16.02162.矩阵的秩
矩阵A中线性无关的列向量个数称为列秩,线性无关的行向量个数称为行秩。在MATLAB中用函数rank()来计算矩阵的秩。函数rank()的用法如下:
- rank(A):用默认允许误差计算矩阵的秩。
- rank(A,tol):给定允许误差计算矩阵的秩,tol=max(size(A))·eps(norm(A))。
例:求矩阵的秩示例
>> A=[1 2 3;3 4 5;7 8 9];
>> B=magic(3);
>> r1=rank(A)%矩阵的秩
r1 =
23.3.
>> r2=rank(B)
r2 =
33.矩阵的行列式
矩阵A={aij}n×n的行列式定义如下:
![]()
其中,k1,k2,…,kn是将序列1,2,…,n交换k次所得的序列。在MATLAB中函数det()来计算矩阵的行列式。
例:计算矩阵的行列式示例
>> A=[1 2 3;3 4 5;7 8 9];
>> B=magic(5);
>> r1=det(A);%矩阵的行列式
>> r2=det(B);
>> disp(['a的行列式=',num2str(r1)]);
a的行列式=0
>> disp(['b的行列式值=',num2str(r2)]);
b的行列式值=50700004.矩阵的迹
矩阵的迹定义为矩阵对角元素之和。在MATLAB中用函数trace()来计算矩阵的迹。
例:计算矩阵的迹示例
>> A=[1 2 3;3 4 5;7 8 9];
>> B=magic(5);
>> r1=trace(A);%矩阵的迹
>> r2=trace(B);
>> disp(['A的迹=',num2str(r1)]);
A的迹=14
>> disp(['B的迹=',num2str(r2)]);
B的迹=655.矩阵的化零矩阵
MATLAB中提供了求化零矩阵的函数null(),其用法如下:
- Z=null(A):返回矩阵A的一个化零矩阵,如果化零矩阵不存在,则返回空矩阵。
- Z=null(A,’r’):返回有理数形式的化零矩阵。
例:求矩阵的化零矩阵示例
>> A=[1 2 3;3 4 5;7 8 9];
>> Z=null(A)%求矩阵A的化零矩阵
Z =
0.4082
-0.8165
0.4082
>> AZ=A*Z
AZ =
1.0e-14 *
0.0222
-0.0444
-0.1332
>> ZR=null(A,'r')%求矩阵A的有理数形式的化零矩阵
ZR =
1
-2
1
>> AZR=A*ZR
AZR =
0
0
06.矩阵的正交空间
矩阵A的矩阵空间Q具有Q’·Q=I的性质,并且Q的列矢量构成的线性空间与矩阵A的列向量构成的线性空间相同,且正交空间Q与矩阵A具有相同的秩。MATLAB中提供了函数orth()来求正交空间Q。
例:矩阵的正交空间求解示例
>> A=[1 2 3;3 4 5;7 8 9];
>> Q=orth(A)
Q =
-0.2262 -0.8143
-0.4404 -0.4040
-0.8688 0.41687.矩阵的约化行阶梯形式
矩阵的约化行阶梯形式是高斯-约旦消去法解线性方程组的结果.
MATLAB中提供了函数rref()来求矩阵的约化行阶梯形式,其用法如下:
- R=rref(A):返回矩阵A的约化行阶梯形式R。
- [R,jb]=rref(A):返回矩阵A的约化行阶梯形式R,并返回1×r的向量jb,r为矩阵A的秩;A(:,jb)是矩阵A的列矢量构成的线性空间;R=(1:r,jb)是r×r的单位矩阵。
- [R,jb]=rref(A,tol):以tol作为允许的相对误差计算矩阵A的秩。
例:求矩阵A的约化行阶梯形式示例
>> A=[1 2 3;4 5 6;7 8 9;10 11 12];%矩阵A
>> R=rref(A)%正交矩阵A的约化行阶梯形式
R =
1 0 -1
0 1 2
0 0 0
0 0 08.矩阵空间之间的夹角
矩阵空间之间的夹角代表两个矩阵线性相关的程度。如果夹角很小,它们之间的线性相关度就很高;反之,它们之间的线性相关度就很低。在MATLAB中用函数subspace(0来实现求矩阵空间之间的夹角,其调用格式如下:
- thera=subspace(A,B):返回矩阵A和矩阵B之间的夹角。
例:求矩阵A和矩阵B之间的夹角示例
>> A=[1 2 3;3 4 5;7 8 9;8 7 9;0 2 8];
>> B=magic(5);
>> subspace(A,B)
ans =
9.6980e-162.4.2矩阵分解
矩阵分解是把一个矩阵分解成几个“较简单”的矩阵连乘形式。无论是在理论上还是在工程应用上,矩阵分解都是十分重要的。

在MATLAB中,线性方程组的求解主要基于4种矩阵分解,即对称正定矩阵的Cholesky分解、一般方阵的高斯消去法分解、矩形矩阵的正交分解和舒尔分解。
1.对称正定矩阵的Cholesky分解
Cholesky分解在MATLAB种用函数chol()函数来实现,器常用的调用方式如下:
- R=chol(X):其中X为对称正定矩阵,R是上三角矩阵,使得X=R’·R。如果X是非正定的,则结果将返回出错信息。
- [R,p]=chol(X):返回两个参数,并且不会返回出错信息。当X是正定矩阵时,返回的上三角矩阵R满足X=R’·R,且p=0;当X是非正定矩阵时,返回值p是正整数,R是上三角矩阵,其阶数为p-1,且满足X(1:p-1,1:p-1)=R’·R。
考虑线性方程则Ax=b,其中A可以做Cholesky分解,使得A=R’·R,这样线性方程组就可以改写成R’·Rx=b。由于左除运算符“\”可以快速处理三角矩阵,因此得出:
x=R\(R’\b)
其中A是n×n的方阵,则chol(A)的计算复杂度是O(n3),而左除运算符“\”的计算复杂度只要O(n2)。
例:利用chol函数进行矩阵分解示例
>> A=pascal(5)%产生5阶帕斯卡矩阵
A =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70
>> eig(A)
ans =
0.0108
0.1812
1.0000
5.5175
92.2904
>> R=chol(A)
R =
1 1 1 1 1
0 1 2 3 4
0 0 1 3 6
0 0 0 1 4
0 0 0 0 1
>> R'*R
ans =
1 1 1 1 1
1 2 3 4 5
1 3 6 10 15
1 4 10 20 35
1 5 15 35 70例:计算稀疏矩阵的Cholesky因子,并使用置换输出创建具有较少非零元素的Cholesky因子
>> load west0479;%基于west0479矩阵创建一个系数正定矩阵
A=west0479;
S=A'*A;
%用两种不同的方法计算矩阵的Cholesky因子。首先指定两个输出,然后指定三个输出以支持行和列重写排序
>> [R,flag]=chol(S);
>> [RP,flagP,P]=chol(S);
>> if ~flag&&~flagP%对于每次计算,都检查flag=0以确认计算成功
disp('Factorization successful.')
else
disp('Factorizations failed.')
end
Factorization successful.
>> %比较chol(S)和经过重新排序的矩阵chol(P'*S*P)中非零元素的个数
>> subplot(1,2,1)
spy(R)
>> title('Nonzeors in chol(S)')
>> subplot(1,2,2)
>> spy(RP)
>> title('Nonzeros in chol(P''*S*P)')
2.一般方阵的高斯消去法分解
高斯消去法分解又称LU分解,它可以将任意一个方阵A分解为一个下三角矩阵L和一个上三角矩阵U的成绩,即A=LU。LU分解在MATLAB中用函数lu()函数来实现,其调用方式如下:
(1)[L,U]=lu(X):X为一个方阵,L为下三角矩阵,U为上三角矩阵,满足关系X=L·U。
(2)[L,U,P]=lu(X):X为一个方阵,L为下三角矩阵,U为上三角矩阵,P为置换矩阵,妈祖关系P·X=L·U。
(3)Y=lu(X):X为一个方阵,把上三角矩阵和下三角矩阵合并在矩阵Y中给出,矩阵Y的对角元素为上三角矩阵的对角元素,即Y=L+U-I。置换矩阵P的信息矩阵。
考虑线性方程组Ax=b,其中,对矩阵A可以做LU分解,使得A=LU,这样线性方程组就可以改写成LUx=b。由于左除运算符“\”可以快速处理三角矩阵,因此可以快速解出:
x=U\(L\b)
利用LU分解来计算行列式的值和矩阵的逆,其命令形式如下:
- det(A)=det(L)*det(U)
- inv(A)=inv(L)*inv(U)
例:进行LU分解示例
>> A=[2 4 5;8 9 6;1 3 5];
>> [L1,U1]=lu(A)%矩阵的LU分解
L1 =
0.2500 0.9333 1.0000
1.0000 0 0
0.1250 1.0000 0
U1 =
8.0000 9.0000 6.0000
0 1.8750 4.2500
0 0 -0.4667
>> [L2,U2,P]=lu(A)
L2 =
1.0000 0 0
0.1250 1.0000 0
0.2500 0.9333 1.0000
U2 =
8.0000 9.0000 6.0000
0 1.8750 4.2500
0 0 -0.4667
P =
0 1 0
0 0 1
1 0 0
>> Y1=lu(A)
Y1 =
8.0000 9.0000 6.0000
0.1250 1.8750 4.2500
0.2500 0.9333 -0.4667
>> L1*U1%验证
ans =
2 4 5
8 9 6
1 3 5
>> Y2=L2+U2-eye(size(A))%验证
Y2 =
8.0000 9.0000 6.0000
0.1250 1.8750 4.2500
0.2500 0.9333 -0.4667此外,对于稀疏矩阵,MATLAB提供了函数luinc()来做不完全LU分解,其调用格式如下:
(1)[L,U]=luinc(X,DROPTOL):其中X、L和U的含义与函数lu()中的变量相同,DROPTOL为不完全LU分解的丢失容限。当DROPTOL设为0时,退化为完全LU分解。
(2)[L,U]=luinc(X,OPTS):其中OPTS为结构体,它有四个属性,即DROPTOL、MICHOL、RDIAG和THRESH。DROPTOL为不完全LU分解的丢失容限;当MICHOL为1时,采用改进算法的不完全LU分解,否则不采用改进算法;当RDIAG为1时,R的对角元素中的零值替换成DROPTOL的平方根,当其为0时不做此替换;THRESH是绕对角线旋转因子,其取值范围是[0,1],当THRESH为0时强制绕对角线旋转,THRESH的默认值是1.
(3)[L,U,P]=luinc(X,’0’):0级不完全LU分解。
(4)[L,U]=luinc(X,’0’):0级不完全LU分解。
(5)Y=luinc(X,’0’):0级完全LU分解。
3.矩形矩阵的正交分解
矩形矩阵的正交分解又称QR分解,QR分解把一个m×n的矩阵A分解为一个正交矩阵Q和一个上三角矩阵R的乘积,即A=Q·R。在MATLAB中QR分解由函数qr()来实现。QR的调用方式如下:
(1)[Q,R]=qr(A):其中矩阵R为与矩阵A具有相同大小的上三角矩阵,Q为正交矩阵,它们满足A=Q·R。该调用方式适用于满矩阵和稀疏矩阵。
(2)[Q,R]=qr(A,0):为“经济”方式的QR分解。设矩阵A是一个m×n的矩阵,若m>n,则只计算矩阵Q的前n列元素,R为n×n的矩阵;若m≤n,则于[Q,R]=qr(A)效果一致。该调用方式适用于满矩阵和稀疏矩阵。
(3)[Q,R,E]=qr(A):R是上三角矩阵,Q为正交矩阵,E为置换矩阵,它们满足A·E=Q·R。程序选择一个合适的矩阵E使得abs(diag))是降序排序的。该调用方式适合于满矩阵。
(4)[Q,R,E]=qr(A,0):为“经济”方式的QR分解,其中E是一个置换矢量,它们满足A(:E)=Q`R。该调用方式适用于满矩阵。
(5)R=qr(A):返回上三角矩阵R,这里R=chol(A’·A)。该调用方式适用于稀疏矩阵。
(6)R=qr(A,0):以“经济”方式返回上三角矩阵R。
(7)[C,R]=qr(A,B):其中矩阵B必须与矩阵A具有相同的行数,矩阵R是上三角矩阵,C=Q’·B。
例:提供QR分解矩阵的秩示例
>> A=[2 4 5;8 9 6;1 3 5];
>> [Q1,R1]=qr(A)
Q1 =
-0.2408 0.6424 -0.7276
-0.9631 -0.2511 0.0970
-0.1204 0.7241 0.6791
R1 =
-8.3066 -9.9920 -7.5843
0 2.4818 5.3257
0 0 0.3395
>> B=[2 4 5;8 9 6;5 4 10];
>> B_rank=rank(B);
>> disp(['矩阵B的秩=',num2str(B_rank)]);
矩阵B的秩=3
>> [Q2,R2]=qr(B)
Q2 =
-0.2074 0.7905 0.5762
-0.8296 0.1701 -0.5319
-0.5185 -0.5883 0.6205
R2 =
-9.6437 -10.3695 -11.1991
0 2.3395 -0.9100
0 0 5.8951
>> Q1*R1
ans =
2.0000 4.0000 5.0000
8.0000 9.0000 6.0000
1.0000 3.0000 5.00004.舒尔分解
舒尔分解定义式为:
A=U·S·U’
其中A必须是一个方阵,U是一个酉矩阵,S是一个块对角矩阵,由对角线上的1×1和2×2块组成。特征值可以由矩阵S的对角块给出,而矩阵U给出比特征向量更多的数值特征。此外,对缺陷矩阵也可以进行舒尔分解。MATLAB中用函数schur()来进行舒尔分解,其调用格式如下:
(1)[U,S]=schur(A):返回酉矩阵U和对角块矩阵S。
(2)S=schur(A):仅返回对角块矩阵S。
(3)schur(A,’real’):返回的实特征值放在对角线上,而把复特征值放在对角线上的2×2块中。
(4)schur(A,’complex’):返回矩阵S是上三角矩阵,并且如果矩阵A有复特征值,则矩阵S是复矩阵。
另外,函数rsf2csf()可以把实数形式的舒尔矩阵转换成复数形式的舒尔矩阵。
例:舒尔分解示例
>> A=pascal(5);
>> [U,S]=schur(A)
U =
0.1680 -0.5706 -0.7660 0.2429 0.0175
-0.5517 0.5587 -0.3830 0.4808 0.0749
0.7025 0.2529 0.1642 0.6110 0.2055
-0.4071 -0.5179 0.4377 0.4130 0.4515
0.0900 0.1734 -0.2189 -0.4074 0.8649
S =
0.0108 0 0 0 0
0 0.1812 0 0 0
0 0 1.0000 0 0
0 0 0 5.5175 0
0 0 0 0 92.2904
>> U*S-A%验证
ans =
-0.9982 -1.1034 -1.7660 0.3404 0.6143
-1.0060 -1.8987 -3.3830 -1.3472 1.9142
-0.9924 -2.9542 -5.8358 -6.6289 3.9633
-1.0044 -4.0939 -9.5623 -17.7211 6.6726
-0.9990 -4.9686 -15.2189 -37.2476 9.81792.4.3 特征值和特征向量
1.特征值和特征向量的定义
MATLAB中的命令计算特征值和特征向量十分方便,可以得到不同的子结果和分解,这在线性代数学习中十分有意义。
假设A是一个n×n的矩阵,A的特征值问题就是找到下面方程组的解:
A·V=λ·V
其中,λ为标量,V为矢量,若把矩阵A的n个特征值放在矩阵P的对角线上,相应的特征向量按照与特征值对应的顺序排列,作为矩阵V的列,则特征值问题可以改写为:
A·V=V·D
如果V是非奇异的,则该问题可以认为是一个特征值分解问题,此时关系式如下:
A=V ·D·V-1
广义特征值问题是指方程Ax=λBx的非平凡解问题,其中A、B都是n×n的矩阵,λ为标量。满足此方程的λ为广义特征值,对应的向量x为广义特征向量。
如果X是一个列向量为a的特征向量的矩阵,并且它的秩为n,那么特征向量线性无关。如果不是这样,则称矩阵是缺陷阵。如果X’X=I,则特征向量正交,这对于对称矩阵是成立的。
2.特征值和特征向量的相关函数
现将MATLAB中矩阵特征值与特征向量的相关函数的具体调用格式及功能列出。
- eig(A):求包含矩阵A的特征值的向量。
- [X,D]=eig(A):产生一个矩阵A的特征值在对角线上的对角矩阵D和矩阵X,它们的列是相应的特征向量,。满足AX=XD。为了得到有更好条件特征值的矩阵,要进行相似变换。
- [T,B]=balance(A):找到一个相似变换矩阵T和矩阵B,使得它们满足B=T-A·T。B是用命令balance求得平衡矩阵。
- eig(A,’nobalance’):不经过平衡处理求得矩阵你A的特征值和特征向量,也就是不进行平衡相似变换。
- eigs(A):返回一个由矩阵A的部分特征值组成的向量,和eig命令一样,但是不返回全部的特征值。如果不带有参量,则计算出最大的特征值。当计算所有特征值时,如果矩阵A的秩不小于6,则计算出6个特征值。
- eigs(f,n):求出矩阵A的部分特征值。在使用一个矩阵列的线性运算符时,字符串f中包含的是M文件的文件名 ,n指定问题的阶次。用这种方法来求特征值比开始就用运算符来求要快。
- eigs(A,B,sigma):求矩阵A的部分特征值,矩阵B的大小和A相同;如果没有给出B=eye(size(A)),那么k就要计算的特征值的个数;如果k没有给出,就用小于6的数或者A的秩。
变量sigma是一个实数或复数的移位参数,或者下列文本字符串的一个,文本字符串知名的是特征值德 属性:“lm”为最大德特征值,“sm”为最小的特征值,“Ir”为最大的实数部分,“sr”为最小的实数部分,“be”为同时求得最大和最小的实数部分。
- condeig(A):返回一个由矩阵A的特征值体哦阿健数组成的向量。
- [V,D,s]=comdeig(A):返回[V,D]=eig(A)和s=condeig(A)。
3.特征值和特征向量的计算
例:矩阵特征值和特征向量的计算示例
>> A=[0.8,0.2;0.2,0.8];
>> [Q,d]=eig(A)
Q =
-0.7071 0.7071
0.7071 0.7071
d =
0.6000 0
0 1.0000
>> Q*Q'
ans =
1.0000 0
0 1.00002.5稀疏矩阵
在许多问题中提到了含有大量0元素的矩阵,这样的矩阵称为稀疏矩阵。为了节省存储空间和计算时间,MATLAB考虑到矩阵的稀疏性,在对它进行运算时有特殊的命令。
一个稀疏矩阵中有很多元素等于0,这便于矩阵的计算和存储,如果MATLAB把一个矩阵当作稀疏矩阵,那么只需在m×3的矩阵中存储m个非零项。第一列是行下标,第二列是列下标,第三列是非零元素值,不必保存0元素。如果存储每个浮点数需要八个字节,在存储每个下标需要4个字节,那么整个矩阵在内存中存储需要16×m字节。
例:稀疏矩阵与普通矩阵示例
>> A=eye(1000);%得到一个1000×1000的单位矩阵
>> B=speye(1000);%得到一个100×3的矩阵,每行包含行下标、列下标及元素本身稀疏矩阵大部分元素都是0,因此只需存储非零元素的下标和元素值,这种特殊的存储方式可以节省大量的存储空间和不必要的运算。
2.5.1稀疏矩阵的存储方式
对于稀疏矩阵,MATLAB仅存储矩阵所有非零元素的值和下标。显然,这对于具有大量0元素的稀疏矩阵来说十分有效。
2.5.2 稀疏矩阵的生成
MATLAB中提供了多种创建稀疏矩阵的方法。
- 利用sparse函数由满矩阵转换得到稀疏矩阵。
- 利用一些特定函数包括单位稀疏矩阵在内的特殊稀疏矩阵。
1.利用sparse函数创建一般系数矩阵
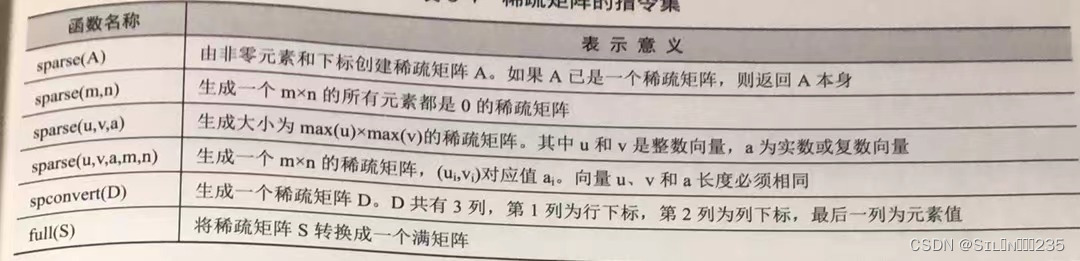
例:输入一个稀疏矩阵示例
>> S=sparse([1,2,3,4,5],[2 1 4 6 2],[10 3 -2 -5 -1],10,12)
S =
(2,1) 3
(1,2) 10
(5,2) -1
(3,4) -2
(4,6) -5此外,sparse函数还可以将一个满矩阵转换成一个稀疏矩阵,相应的调用格式如下:
S=sparse(X):X为满矩阵
例如矩阵A=[1 0 0 0;0 5 0 0;2 0 0 7]。
>> A=[1 0 0 0;0 5 0 0;2 0 0 7]
A =
1 0 0 0
0 5 0 0
2 0 0 7
>> S=sparse(A)
S =
(1,1) 1
(3,1) 2
(2,2) 5
(3,4) 7反之,MATLAB中提供了full()函数把系数矩阵转换为满矩阵。full()函数的调用函数如下:
A=full(S):S为稀疏矩阵。
将上例中得到的稀疏矩阵转换成满矩阵。
>> B=full(S)
B =
1 0 0 0
0 5 0 0
2 0 0 7例:将普通矩阵转换为稀疏矩阵示例
>> A=rand(16,9)>0.95
A =
16×9 logical 数组
0 0 0 0 0 0 0 0 0
0 0 0 0 1 0 0 0 0
0 0 0 0 0 0 0 0 0
0 1 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 1 0
0 0 1 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
1 0 0 1 0 0 0 0 0
1 0 0 0 0 0 0 1 0
0 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0
1 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
0 0 0 0 0 0 0 0 0
>> S=sparse(A)%创建稀疏矩阵
S =
16×9 稀疏 logical 数组
(9,1) 1
(10,1) 1
(12,1) 1
(13,1) 1
(4,2) 1
(7,3) 1
(9,4) 1
(2,5) 1
(6,8) 1
(10,8) 1
>> whos
Name Size Bytes Class Attributes
A 16x9 144 logical
S 16x9 170 logical sparse 例:查看稀疏矩阵中非零元素的信息示例
>> a=[0 0 0 1;0 0 8 0;4 0 0 0;0 0 0 0];
>> S=sparse(a)%创建稀疏矩阵
S =
(3,1) 4
(2,3) 8
(1,4) 1
>> whos;
Name Size Bytes Class Attributes
A 16x9 144 logical
S 4x4 88 double sparse
a 4x4 128 double
>> n1=nnz(S)%查看非零元素的个数
n1 =
3
>> n2=nonzeros(S)%查看非零元素的值
n2 =
4
8
1
>> n3=nzmax(S)%查看稀疏矩阵的存储空间
n3 =
3
>> spy(S)
>> n4=nnz(S)/prod(size(S))
n4 =
0.1875利用spy()函数可以对稀疏矩阵中非零元素的分布进行图形化显示。

采用nnz(S)/prod(size(S))计算稀疏矩阵的非零元素密度。
2.利用特定函数创建特殊稀疏矩阵


例:利用speye函数创建单位稀疏矩阵示例
>> A=speye(5)%创建5阶单位稀疏矩阵
A =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
(5,5) 1
>> B=speye(5,6)%创建5×6的稀疏矩阵
B =
(1,1) 1
(2,2) 1
(3,3) 1
(4,4) 1
(5,5) 1
>> C=full(A)
C =
1 0 0 0 0
0 1 0 0 0
0 0 1 0 0
0 0 0 1 0
0 0 0 0 1
>> D=full(B)
D =
1 0 0 0 0 0
0 1 0 0 0 0
0 0 1 0 0 0
0 0 0 1 0 0
0 0 0 0 1 0例:创建非零元素为随机数的对称稀疏矩阵示例
>> A=sprandsym(5,0.1)%创建非零元素为随机数的对称稀疏矩阵
A =
(2,1) -2.0122
(1,2) -2.0122
>> B=spones(A)%创建非零元素为1的与矩阵A维数相同的对称稀疏矩阵
B =
(2,1) 1
(1,2) 1
>> C=full(A)
C =
0 -2.0122 0 0 0
-2.0122 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 0
>> D=full(B)
D =
0 1 0 0 0
1 0 0 0 0
0 0 0 0 0
0 0 0 0 0
0 0 0 0 02.5.3稀疏矩阵的运算
满矩阵的四则运算对稀疏矩阵同样有效,但是反悔哦的结果有可能是稀疏矩阵或满矩阵。
对于单个稀疏矩阵的输入,大部分函数输出的结果都是稀疏矩阵,有部分函数输出的结果是满矩阵。对于多个矩阵的输入,如果其中至少有一个矩阵是满矩阵,那么大部分函数的输出结果都是满矩阵。
对于矩阵的加、减、乘、除运算,只要其中有一个矩阵是满矩阵,输出结果都是满矩阵。
稀疏矩阵的数乘都是稀疏矩阵,稀疏矩阵的幂都是稀疏矩阵。




![[已解决]npm淘宝镜像最新官方指引(2023.08.31)](https://img-blog.csdnimg.cn/direct/eb7d9c2019a9461ab759da8c3ddffe5f.png)