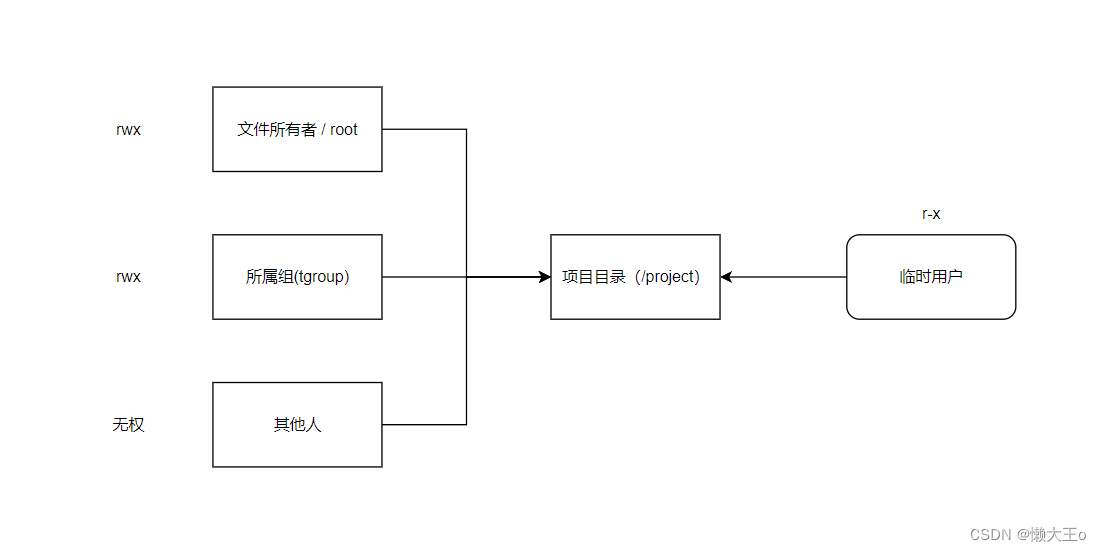
给定一个含有 n 个正整数的数组和一个正整数 target 。

找出该数组中满足其总和大于等于 target 的长度最小的 连续子数组 [numsl, numsl+1, ..., numsr-1, numsr] ，并返回其长度。如果不存在符合条件的子数组，返回 0 。

示例 1：

输入：target = 7, nums = [2,3,1,2,4,3]
输出：2
解释：子数组 [4,3] 是该条件下的长度最小的子数组。

示例 2：

输入：target = 4, nums = [1,4,4]
输出：1

示例 3：

输入：target = 11, nums = [1,1,1,1,1,1,1,1]
输出：0

提示：

• 1 <= target <= 109
• 1 <= nums.length <= 105
• 1 <= nums[i] <= 105

思路

暴力枚举除外，想要找出连续并且相加大于target的最短的字串，至少需要两个指针进行遍历，一个在前一个在后。

第一个针对枚举次数的优化，left指针定住，right往右走，每定义sum，每次加等right，大于traget后就可以停止遍历了，因为要找最短，right再往后只会找到更长的，此时单趟遍历结束。

此时可以直接让left右移 sum-=nums[left];再次比较此时子串和是否大于target，因为有可能右移之后依然>=target,此时len还变短了，如果不符合条件再开始下一趟遍历，然后继续找符合要求的字串，找到后和原本的len进行比较，如果比原来的len小就更新比原来大就移动left然后重复上述操作。

此时可以发现，left和right和通常意义下的双指针不同，不是都向内移动，而是同向进行移动，此时，这种方法就叫做同向双指针，也叫做，滑动窗口。 就像一个随时在变的窗口一样，left是窗口左边，right是窗口右边，每次right移动可以比作进窗口，left移动可以比作出窗口。总结一下就以下三步。

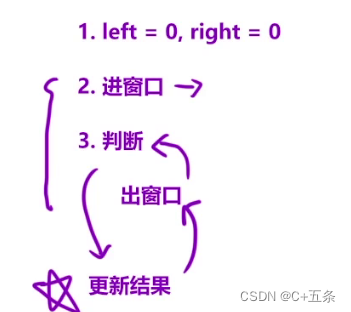
代码实现复杂度O(n)

虽然套了两次循环，但时间复杂度可不是O(n^2),因为每次不管是left动还是right动，整个窗口都是在向右移动，不会再出现左移，此时最差的情况也就是right一直走走到结尾然后left一直走走到结尾。

即便如此复杂度依然为2N.

while循环

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) 
    {
        int left=0,right=0,len=0;
        int sum=0;
        int len1=0;
        while(left<(nums.size()))
        {
            if(right<nums.size()) sum+=nums[right];//入窗口
            else
            {
                if(sum<=target) break;
                //如果right走到结尾此时sum依然小于target直接break，因为窗口值只会越来越小
            }
            while(sum>=target)//判断大于target
            {
                len1=right-left+1;
                if(len==0||len1<len)//更新结果
                {
                    len=len1;
                }
                sum-=nums[left++];//出窗口
            }
            right++;
        }
        return len;
    }
};

for循环

class Solution {
public:
    int minSubArrayLen(int target, vector<int>& nums) 
    {
        int left=0,right=0,len=0;
        int sum=0;
        int len1=0;
        for(int left=0,right=0;right<nums.size();right++)
        {
            sum+=nums[right];
            while(sum>=target)
            {
                len1=right-left+1;
                if(len1<len||len==0)
                {
                    len=len1;
                }
                sum-=nums[left++];
            }
            
        }
        return len;
    }
};