将数字变成0的操作次数
1.题目
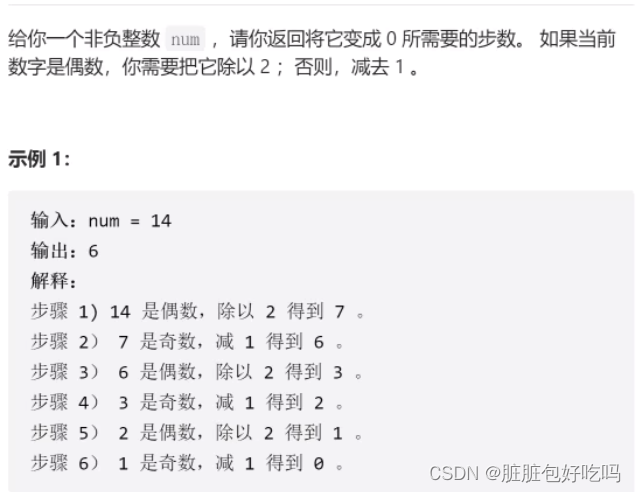
2.思路
在numberOfSteps函数中,首先设置f[0]为0,因为0已经是0了,不需要任何步骤。然后,使用一个for循环从1迭代到输入的整数num。对于每个整数i,如果i是奇数,则将f[i]设置为f[i-1] + 1,表示将i变为0需要先将i-1变为0,然后再执行一次减1操作。如果i是偶数,则将f[i]设置为f[i/2] + 1,表示将i变为0需要先将i/2变为0,然后再执行一次除以2的操作。
最后,main函数从用户那里获取一个整数输入,并调用numberOfSteps函数来计算将该整数变为0所需的步骤数,然后将结果输出到控制台。
3.代码
package 动态规划;
import java.util.Scanner;
public class 将数字变成0 {
static int maxn=1000001;
static int [] f =new int[maxn];
public static int numberOfSteps(int num) {
f[0]=0;
for(int i=1;i<=num;++i) {
if(i%2==1) {
f[i]=f[i-1]+1;
}
else {
f[i]=f[i/2]+1;
}
}
return f[num];
}
public static void main(String[] args) {
System.out.print("输入:num = ");
Scanner sc= new Scanner(System.in);
int num=sc.nextInt();
System.out.print("输出: "+numberOfSteps(num));
}
}
4.知识
重点是 清楚 奇偶情况下的运算代码
f[0]=0;
for(int i=1;i<=num;++i) {
if(i%2==1) {
f[i]=f[i-1]+1;
}
else {
f[i]=f[i/2]+1;
}
}爬楼梯的最少成本
1.题目
数组的每个下标作为一个阶梯,第i个阶梯对应着一个非负数的体力花费值cost[i],下标从0开始。每当爬上一个阶梯都要花费对应的体力值,一旦支付了相应的体力值,就可以选择向上爬一个阶梯或者爬两个阶梯。请找出达到楼层顶部的最低花费。在开始时,你可以选择从下标为0或1的元素作为初始阶梯
2.思路
到达最后一个阶梯的最低花费就是到达倒数第二个阶梯的最低花费和到达最后一个阶梯的花费之和
或者就是到达倒数第一个阶梯的最低花费和到达最后一个阶梯的花费之和
3.代码
public class 爬楼梯的最少成本 {
public static int minCost(int[] cost) {
if(cost==null||cost.length==0) {
return 0;
}
if(cost.length==1) {
return cost[0];
}
//dp[i] 表示到达第i个阶梯的最低花费
int[] dp=new int[cost.length];
//初始化前有两个阶梯的花费
dp[0]=cost[0];
dp[1]=cost[1];
//填充dp数组
for(int i=2;i<cost.length;i++) {
//到达第i个阶梯的最低花费是到达第i-1个阶梯和
//第i-2个阶梯的最低花费中的最小值加上当前阶梯的花费
dp[i]=Math.min(dp[i-1], dp[i-2]+cost[i]);
}
return Math.min(dp[cost.length-1], dp[cost.length-2]);
}
public static void main(String[] args) {
int[] cost= {10,15,20};
System.out.println(minCost(cost));
}
}
4.知识
//填充dp数组
for(int i=2;i<cost.length;i++) {
//到达第i个阶梯的最低花费是到达第i-1个阶梯和
//第i-2个阶梯的最低花费中的最小值加上当前阶梯的花费
dp[i]=Math.min(dp[i-1], dp[i-2]+cost[i]);
}
return Math.min(dp[cost.length-1], dp[cost.length-2]);
到达最后一个阶梯的最低花费就是到达倒数第二个阶梯的最低花费和到达最后一个阶梯的花费之和 或者就是到达倒数第一个阶梯的最低花费和到达最后一个阶梯的花费之和 。