洛谷 【算法1-6】二分查找与二分答案

news2024/10/6 5:58:03

【算法1-6】二分查找与二分答案 - 题单 - 洛谷 | 计算机科学教育新生态 (luogu.com.cn)

鄙人不才，刷洛谷，迎蓝桥，【算法1-6】二分查找与二分答案 已刷，现将 AC 代码献上，望有助于各位

P2249

【深基13.例1】查找 - 洛谷

题目

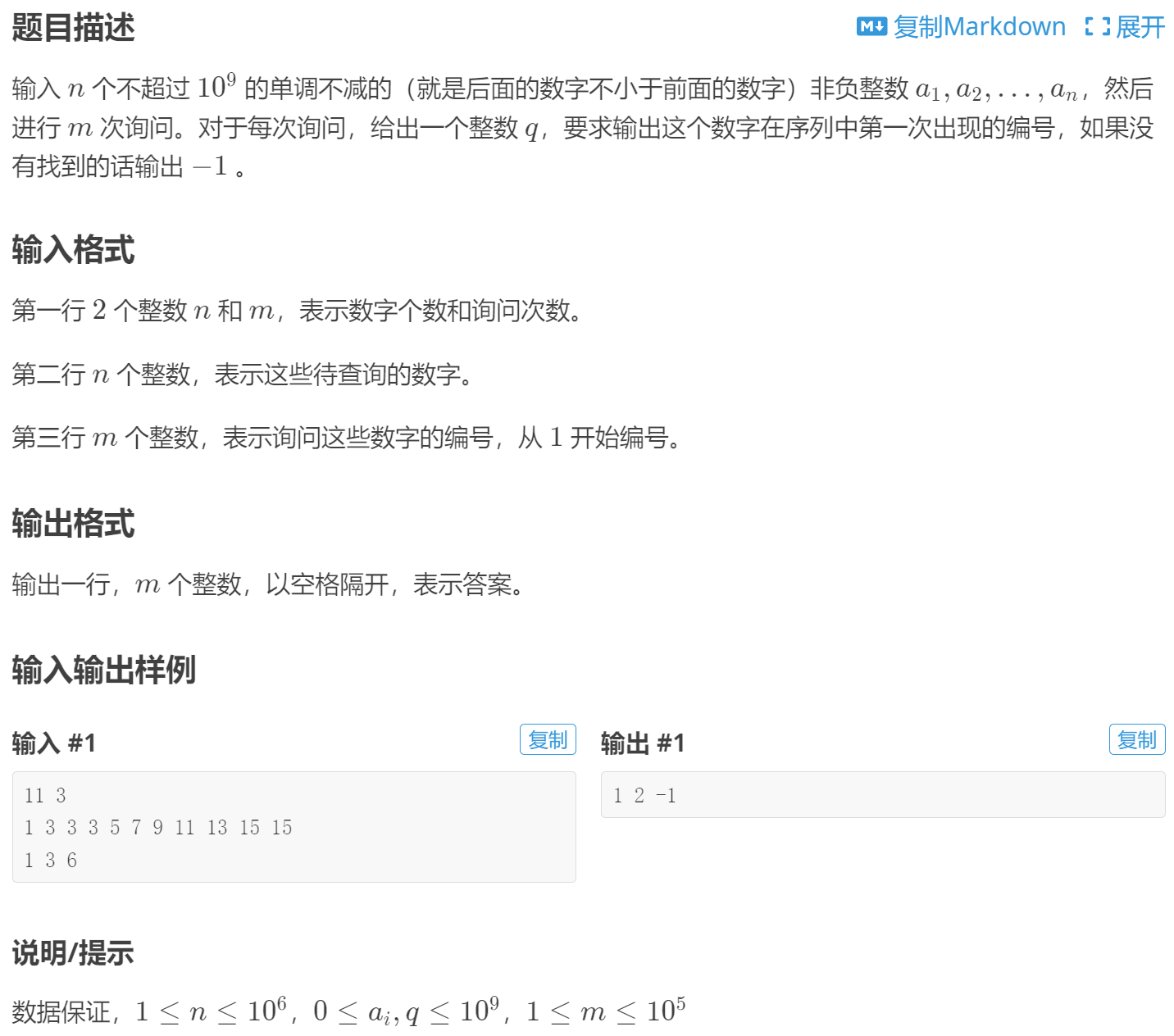
解答

思路

使用二分查找的方式解决

代码

#include<iostream>
using namespace std;
const int N = 1000005;
const int M = 100005;
int a[N], find_n[M];
void search(int aim, int l, int r) {
	if (l >= r && a[l] == aim) {
		cout << l + 1 << " ";
		return;
	}
	if (l >= r) {
		cout << "-1 ";
		return;
	}
	int mid = (l + r) / 2;
	if (aim <= a[mid])
		search(aim, l, mid);
	else
		search(aim, mid + 1, r);
}
int main() {
	int n, m;
	cin >> n >> m;
	for (int i = 0; i < n; i++)
		cin >> a[i];
	for (int i = 0; i < m; i++)
		cin >> find_n[i];
	int q = 0;
	while (q < m) {
		search(find_n[q], 0, n - 1);
		q++;
	}
	
	return 0;
}

P1102 A-B 数对

A-B 数对 - 洛谷

题目

解答

思路

在一个数组中，寻找 A-B=C 的数值对 <A, B>，A-B=C 即 A-C=B ，求与 A 对应的 B 的个数

用 map 映射数组元素出现的次数 <value，times>

代码

#include<iostream>
#include<map>
using namespace std;
const int N = 200005;
long long int q[N], C;
map<int, int> a;
long long int n;
int main() {
	cin >> n >> C;
	for (int i = 0; i < n; i++) {
		cin >> q[i];
		a[q[i]]++;
		q[i] -= C;
	}
	long long int ans = 0;
	for (int i = 0; i < n; i++)
		ans += a[q[i]];
	cout << ans;
	return 0;
}

P1873 KEO / 砍树

[COCI 2011/2012 #5] EKO / 砍树 - 洛谷

题目

解答

思路

二分查找 H，0 ≤ H ≤ max_tree

  1. 排序 tree，寻找 max_tree
  2. 二分查找 H，判断条件为 实际伐木总长度 ＜ m

代码

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 1000005;
int tree[N];
long long int m;
int n;
int main() {
	cin >> n >> m;
	for (int i = 0; i < n; i++)
		cin >> tree[i];
	sort(tree, tree + n);
	int l = 0, r = tree[n - 1];
	while (l <= r) {
		int mid =( l + r )/ 2;
		long long sum = 0;
		for (int i = 0; i < n; i++)
			if (tree[i] > mid)
				sum += (tree[i] - mid);
		if (sum < m)
			r = mid - 1;
		else
			l = mid + 1;
	}
	cout << r;
	return 0;
}

P1024 一元三次方程求解

[NOIP2001 提高组] 一元三次方程求解 - 洛谷

题目

解答

思路

浮点数二分

依据上述定理，使用二分算法求根

代码

#include<iostream>
#include<cstdio>
using namespace std;
double a, b, c, d;
double f(double x) {
	return a * x * x * x + b * x * x + c * x + d;
}
int main() {
	cin >> a >> b >> c >> d;
	int s = 0;
	double l, r, mid, f1, f2;
	for (int i = -100; i < 100; i++) {
		l = i;
		r = l + 1;
		f1 = f(l);
		f2 = f(r);
		if (!f1) {
			printf("%.2lf ", l);
			s++;
		}
		if (f1 * f2 < 0) {
			while (r - l > 0.0001) {
				mid = (l + r) / 2;
				if (f(mid) * f(r) <= 0)
					l = mid;
				else
					r = mid;
			}
			printf("%.2lf ", l);
			s++;
		}
		if (s == 3)
			break;
	}
	return 0;
}

P1678 烦恼的高考志愿

烦恼的高考志愿 - 洛谷

题目

解答

思路

先对学校的预计录取分数排序，然后二分查找每个学生最小的不满意度

代码

#include<iostream>
#include<algorithm>
#include<cmath>
using namespace std;
const int N = 100005;
const int M = 100005;
int m, n;
long long int student[N], school[M];
int main() {
	cin >> m >> n;
	for (int i = 0; i < m; i++)
		cin >> school[i];
	for (int j = 0; j < n; j++)
		cin >> student[j];
	sort(school, school + m);
	long long int ans = 0;
	for (int i = 0; i < n; i++) {//逐个二分
		int l = 0, r = m - 1;
		while (l < r) {
			int mid = (l + r + 1) / 2;
			if (school[mid] <= student[i])
				l = mid;
			else
				r = mid - 1;
		}
		if (student[i] <= school[0])
			ans += (school[0] - student[i]);
		else {
			if (abs(school[l + 1] - student[i]) <= abs(school[l] - student[i]))
				ans += (abs(school[l + 1] - student[i]));
			else
				ans += (abs(school[l] - student[i]));
		}
	}
	cout << ans;
	return 0;
}

P2440 木材加工

木材加工 - 洛谷

题目

解答

思路

二分查找即可

代码

#include<iostream>
#include<algorithm>
using namespace std;
const int N = 100005;
int n;
long long int k;
long long int tree[N];
bool check(long long int a) {
	long long int ans = 0;
	for (int i = 0; i < n; i++)
		ans += tree[i] / a;
	if (ans >= k)
		return true;
	else
		return false;
}
int main() {
	cin >> n >> k;
	for (int i = 0; i < n; i++)
		cin >> tree[i];
	sort(tree, tree + n);
	long long int l = 0, r = tree[n - 1];
	long long int mid;
	while (l + 1 < r) {
		//最终l = 114, r = 115，mid = 114, ans = 7
		//l < r, 继续循环 mid = 114，ans = 7, l = 114……无法退出循环
		mid = (l + r) / 2;
		if (check(mid))
			l = mid;
		else
			r = mid;
	}
	cout << l;
	return 0;
}

P2678 跳石头

[NOIP2015 提高组] 跳石头 - 洛谷

题目

解答

思路

二分查找最短距离的最大值

检测 mid 是否为最短距离？依次遍历相邻两块石头之间的距离，如果出现比 mid 小的距离，则将此块石头搬走，并记录搬走石头的块数；若搬走石头的块数 > m，则说明 mid 比实际的最小距离短，需要使用 mid 更新左边界；若搬走石头的块数 <= m，则说明 mid 比实际的最小距离长，需要使用 mid 更新右边界

代码

#include<iostream>
using namespace std;
long long int l;
const int N = 50005;
const int M = 50005;
int n, m;
long long int ans;
long long int s[N] = { 0 };
long long int max_m = 0, min_m = 0x3f3f3f3f;
bool check(long long int a) {//检测a是否为最短距离
	int count = 0;//count记录拿去石头的块数
	int front = 0;//front表示前一块石头
	for (int i = 1; i <= n + 1; i++) {
		if (s[i] - s[front] < a)//若两块石头之间的距离小于目前的最小距离，则将这块石头拿掉
			count++;
		else
			front = i;
	}
	if (count > m)
		return false;
	else
		return true;
}
int main() {
	cin >> l >> n >> m;
	max_m = l;
	if (m == 0 && n == 0) {//只有起点和终点，中间没有石头的情况
		cout << l;
		return 0;
	}
	for (int i = 1; i <= n; i++) {
		cin >> s[i];
		long long int t = s[i] - s[i - 1];
		if (t < min_m)
			min_m = t;
	}
	s[n + 1] = l;
	if ((s[n + 1] - s[n]) < min_m)
		min_m = s[n - 1] - s[n];
	long long int mid;
	while (min_m <= max_m) {//不能去掉等号，否则少循环一次
		mid = (min_m + max_m) / 2;
		if (check(mid)) {
			ans = mid;
			min_m = mid + 1;//需要搬去的石头数<=m，说明现在的最短距离偏短，需要更大，更新最小边界
		}
		else
			max_m = mid - 1;//需要搬去的石头数>m，说明现在的最短距离>实际的最短距离，需要更小，更新最大边界
	}
	cout << ans;
	return 0;
}

P3853 路标设置

[TJOI2007] 路标设置 - 洛谷

题目

解答

思路

二分查找最长距离的最小值

检测 mid 是否为最长距离？依次遍历相邻两个路障之间的距离，如果出现比 mid 大的距离，则设置新的路障，并记录设置的路障的数量；若新设置的路障数 > k，则说明 mid 比实际的最长距离短，需要使用 mid 更新左边界；若新设置的路障数 <= k，则说明 mid 比实际的最长距离长，需要使用 mid 更新右边界

代码

代码

#include<iostream>
using namespace std;
long long int l;
const int N = 100005;
int k, n;
long long int s[N];
long long int ans;
bool check(long long int mid) {//检测mid是否为最大距离
	int y = k;
	int qian = 0;
	for (int i = 1; i < n; i++) {//遍历原路障，判断此路障与前一个路障直接是否需要安装新的路障
		if (y < 0)
			break;
		if ((s[i] - qian) <= mid)//此路障与前一个路障之间的距离<最大距离，继续遍历
			qian = s[i];
		else {//此路障与前一个路障之间的距离>最大距离，安装路障，新安装的路障与原前一个路障之间的距离为mid
			qian = qian + mid;
			i--;//安装路障之后，不能直接判断原来的下一个路障，还得在此基础上，再次判断此处是否需要再次安装路障
			y--;
		}
	}
	if (y >= 0)
		return true;
	return false;
}
int main() {
	cin >> l >> n >> k;
	for (int i = 0; i < n; i++)
		cin >> s[i];
	long long int min_m = 0, max_m = l;
	while (min_m <= max_m) {
		long long int mid = min_m + (max_m - min_m) / 2;
		if (check(mid)) {
			ans = mid;
			max_m = mid - 1;//需要新设的路障<=k,说明现在的最长距离偏长，需要更短，更新最大边界
		}
		else
			min_m = mid + 1;//需要新设的路障>k,说明现在的最长距离偏短，需要更长，更新最小边界
	}
	cout << ans << endl;
	return 0;
}

P1182 数列分段 SectionⅡ

数列分段 Section II - 洛谷

题目

解答

思路

二分查找子序列和最大值的最小值

检测 mid 是否为子序列和的最大值？依次遍历数组元素，如果出现子序列和 >mid，则将当前元素作为新的子序列的第一个元素；若段数 >= m，则说明 mid 比实际的最大子序列和小，需要使用 mid 更新左边界；若段数 < m，则说明 mid 比实际的最大子序列和大，需要使用 mid 更新右边界

代码

#include<iostream>
using namespace std;
const int N = 100005;
int n, m;
long long int num[N], l = 0, r = 0x3f3f3f3f;
long long int ans;
bool check(long long int mid) {
	int cnt = 0, s = 0;
	for (int i = 0; i < n; i++) {
		if ((s + num[i]) <= mid)
			s += num[i];
		else {
			s = num[i];
			cnt++;
		}
	}
	return cnt >= m;
}
int main() {
	cin >> n >> m;
	for (int i = 0; i < n; i++) {
		cin >> num[i];
		if (l < num[i])
			l = num[i];
		r += num[i];
	}
	while (l <= r) {
		long long int mid = (l + r) / 2;
		if (check(mid))
			l = mid + 1;//实际划分的组数>=要求的组数，说明子序列和偏小，实际子序列和应该更大
		else
			r = mid - 1;//实际划分的组数<要求的组数，说明子序列和偏大，实际子序列和应该更小
	}
	cout << l;
	return 0;
}

P1163 银行贷款

银行贷款 - 洛谷

题目

解答

思路

二分查找月利率，查找的范围大一些，要包含所有的范围

遍历每一个月，每月先计算利息，再还款

还款结束后，若欠债为0，或二分查找范围小于 0.0001 时，表示已经找到月利率；

若存在欠债，说明月利率太大了，使得利息过多

若不存在欠债，且多还款了，说明月利率太小了，使得利息过少

代码

#include<iostream>
using namespace std;
double w_s, w;
double year;
double lx = 0;
double find(double l, double r) {
	double mid = (l + r) / 2;
	double qianzai = w_s;//表示目前的欠债
	for (int i = 0; i < year; i++) 
		qianzai = qianzai * (1 + mid) - w;
	if (qianzai == 0 || r - l < 0.0001)
		return mid;
	if (qianzai < 0)
		return find(mid, r);
	else
		return find(l, mid);
}
int main() {
	cin >> w_s >> w >> year;
	double h = find(0, 5);//二分，开大一点，保证所有数都可以通过
	printf("%.1lf", h * 100);
	return 0;
}

P3743 kotori 的设备

kotori的设备 - 洛谷

题目

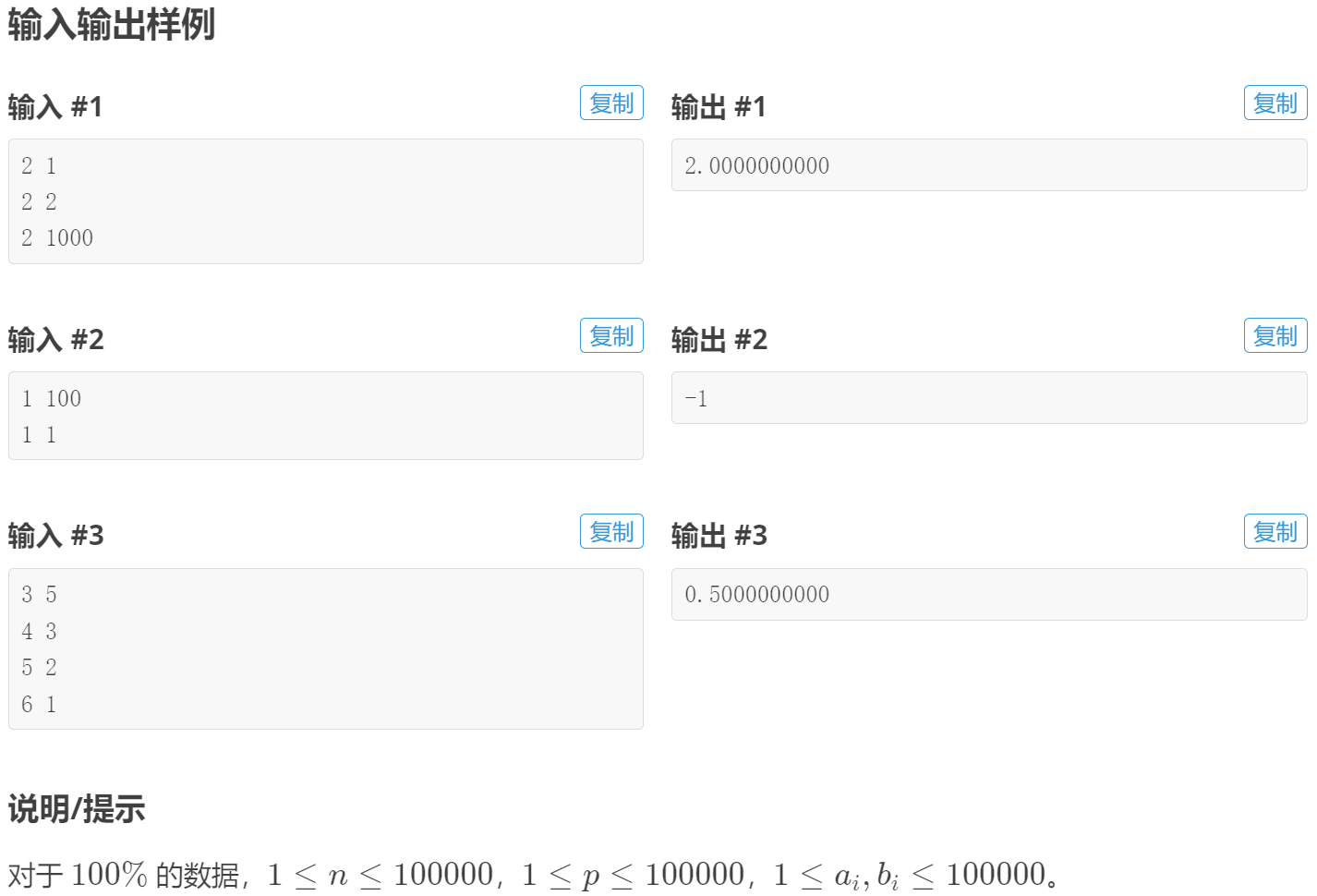
解答

思路

二分查找设备使用时间

特判：用电量<=充电量，可以无限使用

如何查找设备最久使用时间？检测需要的充电量与实际充电量的关系，若需要的充电量<=实际充电量，说明设备使用时间<最久设备使用时间，更新二分的左边界；反之，说明设备使用时间>最久设备使用时间，更新二分的右边界

代码

#include<iostream>
using namespace std;
const int N = 100005;
double p;
int n;
double a[N], b[N];
double sum = 0;//需要的能量
bool check(double mid) {
	double max = p * mid;//max表示充电器最多提供的能力
	sum = 0;
	for (int i = 0; i < n; i++) {//遍历每一台设备
		if ((a[i] * mid) <= b[i])//设备已有的能量>需要的能量
			continue;
		sum = sum + ((a[i] * mid) - b[i]);//计算充电量
	}
	return sum <= max;
}
int main() {
	cin >> n >> p;
	for (int i = 0; i < n; i++) {
		cin >> a[i] >> b[i];
		sum += a[i];
	}
	//特判：无限使用
	if (sum <= p) {
		cout << "-1" << endl;
		return 0;
	}
	double l = 0, r = 1e10;
	while ((r - l) > 0.0001) {
		double mid = (l + r) / 2;
		if (check(mid))//需要的充电量<=实际充电量
			l = mid;
		else
			r = mid;
	}
	cout << l << endl;
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1466838.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

MySQL数据库基础（十三）：关系型数据库三范式介绍

MySQL数据库基础（十三）：关系型数据库三范式介绍

文章目录 关系型数据库三范式介绍 一、什么是三范式 二、数据冗余 三、范式的划分 四、一范式 五、二范式 六、三范式 七、总结 关系型数据库三范式介绍 一、什么是三范式 设计关系数据库时&#xff0c;遵从不同的规范要求&#xff0c;设计出合理的关系型数据库&…
阅读更多...
Clickhouse系列之连接工具连接、数据类型和数据库

Clickhouse系列之连接工具连接、数据类型和数据库

基本操作 一、使用连接工具连接二、数据类型1、数字类型IntFloatDecimal 2、字符串类型StringFixedStringUUID 3、时间类型DateTimeDateTime64Date 4、复合类型ArrayEnum 5、特殊类型Nullable 三、数据库 一、使用连接工具连接 上一篇介绍了clickhouse的命令行登录&#xff0c…
阅读更多...
数字滚动实现

数字滚动实现

介绍 vue-countup-v3 插件是一个基于 Vue3 的数字动画插件&#xff0c;用于在网站或应用程序中创建带有数字动画效果的计数器。通过该插件&#xff0c;我们可以轻松地实现数字的递增或递减动画&#xff0c;并自定义其样式和动画效果。该插件可以用于许多场景&#xff0c;例如展…
阅读更多...
ELK介绍以及搭建

ELK介绍以及搭建

基础环境 hostnamectl set-hostname els01 hostnamectl set-hostname els02 hostnamectl set-hostname els03 hostnamectl set-hostname kbased -i s/SELINUXenforcing/SELINUXdisabled/ /etc/selinux/config systemctl stop firewalld & systemctl disable firewalld# 安…
阅读更多...
pytest结合Allure生成测试报告

pytest结合Allure生成测试报告

文章目录 1.Allure配置安装2.使用基本命令报告美化1.**前置条件**2.**用例步骤****3.标题和描述****4.用例优先级**3.进阶用法allure+parametrize参数化parametrize+idsparametrize+@allure.title()4.动态化参数5.环境信息**方式一****方式二**6.用例失败截图1.Allure配置安装 …
阅读更多...
【深度学习】微调通义千问模型：LoRA 方法，微调Qwen1.8B教程，实践

【深度学习】微调通义千问模型：LoRA 方法，微调Qwen1.8B教程，实践

官网资料: https://github.com/QwenLM/Qwen/blob/main/README_CN.md 文章目录 准备数据运行微调设置网络代理启动容器执行 LoRA 微调修改 finetune/finetune_lora_single_gpu.sh运行微调 执行推理 在本篇博客中&#xff0c;我们将介绍如何使用 LoRA 方法微调通义千问模型&#…
阅读更多...
Qt_快速安装指南

Qt_快速安装指南

下载Qt在线安装程序&#xff08;不仔细介绍&#xff09;注册Qt账号&#xff08;不仔细介绍&#xff09;使用快速运行的命令&#xff0c;按照指定的下载地址下载 在Qt指定目录打开cmd命令窗口.\eqt-unified-windows-x86-4.0.1-1-online. exe --mirror https://mirrors.ustc.edu.…
阅读更多...
C++：派生类的生成过程（构造、析构）

C++：派生类的生成过程（构造、析构）

目录 派生类的生成过程 派生类的构造函数与析构函数&#xff1a; 构造函数&#xff1a; 派生类组合类的构造和析构&#xff1a; 构造函数和析构函数调用顺序&#xff1a; 派生类的生成过程 三步骤&#xff1a; 吸收基类&#xff08;父类&#xff09;成员&#xff1a;实现代…
阅读更多...
多输入时序预测|GWO-CNN-LSTM|灰狼算法优化的卷积-长短期神经网络时序预测(Matlab)

多输入时序预测|GWO-CNN-LSTM|灰狼算法优化的卷积-长短期神经网络时序预测(Matlab)

目录 一、程序及算法内容介绍&#xff1a; 基本内容&#xff1a; 亮点与优势&#xff1a; 二、实际运行效果&#xff1a; 三、算法介绍&#xff1a; 灰狼优化算法&#xff1a; 卷积神经网络-长短期记忆网络&#xff1a; 四、完整程序下载&#xff1a; 一、程序及算法内容…
阅读更多...
CLion 2023：专注于C和C++编程的智能IDE mac/win版

CLion 2023：专注于C和C++编程的智能IDE mac/win版

JetBrains CLion 2023是一款专为C和C开发者设计的集成开发环境&#xff08;IDE&#xff09;&#xff0c;它集成了许多先进的功能&#xff0c;旨在提高开发效率和生产力。 CLion 2023软件获取 CLion 2023的智能代码编辑器提供了丰富的代码补全和提示功能&#xff0c;使您能够更…
阅读更多...
snmp协议开通教程

snmp协议开通教程

目录 一、什么是snmp协议&#xff1f; 二、snmp协议可以用来干什么&#xff1f; 三、snmp协议的开通 1、snmpv2协议开通 2、snmpv3协议开通 一、什么是snmp协议&#xff1f; SNMP&#xff08;Simple Network Management Protocol&#xff09;是一种用于网络管理的标准协议&a…
阅读更多...
软件测试总结报告.doc

软件测试总结报告.doc

编写测试总结报告主要有以下几个目的&#xff1a; 1&#xff0e; 通过对系统测试结果分析&#xff0c;确保软件质量符合交付要求。 2&#xff0e; 分析测试的过程&#xff0c;产品&#xff0c;资源&#xff0c;信息&#xff0c;为以后的其他测试制定测试计划提供参考。 3&#…
阅读更多...
【 JS 进阶 】Web APIs （一）

【 JS 进阶 】Web APIs （一）

“生命是一曲奇妙的交响&#xff0c;每一段都是挑战&#xff0c;每一个音符都是机遇。在激情的旋律中&#xff0c;用勇气弹奏&#xff0c;创造出属于自己的华彩人生。” - 贝多芬 了解 DOM 的结构并掌握其基本的操作&#xff0c;体验 DOM 的在开发中的作用 知道 ECMAScript 与 …
阅读更多...
【Python如何求出水仙花数】

【Python如何求出水仙花数】

1、求水仙花数Python代码如下&#xff1a; # 求水仙花数&#xff1a;只需要个十百位的3次幂之和与原数相等 for i in range(100, 1000): # 循环100-999整数i1 i % 10 # 取个位 “%”表示除以后取余数i2 i // 10 % 10 # 取十位i3 i // 100 # 取百位 “//”表示除以后取整…
阅读更多...
node.js使用multer在vue中实现图片上传

node.js使用multer在vue中实现图片上传

效果演示 点击上传选择要上传的图片。 上传成功会加载图片的缩略图。 此时&#xff0c;图片以保存在后端的静态目录中。 设计思路 vue中使用input标签上传图片&#xff0c;绑定change事件&#xff0c;事件负责把图片发送给后端&#xff0c;后端通过multer模块处理前端传来的…
阅读更多...
通俗易懂理解CA(Coordinate Attention)

通俗易懂理解CA(Coordinate Attention)

一、参考资料 github代码&#xff1a;CoordAttention Coordinate Attention 二、相关介绍 通道注意力与空间注意力 关于通道注意力和空间注意力的详细介绍&#xff0c;请参考另一篇博客&#xff1a;通俗易懂理解通道注意力机制(CAM)与空间注意力机制(SAM) 注意力机制是用…
阅读更多...
8、电源管理入门之休眠唤醒

8、电源管理入门之休眠唤醒

目录 1.基本概念和框架 1.1 基本概念 1.2 休眠唤醒技术框架 2. 核心代码分析 3. 详细分析 3.1 suspend sys节点入口 3.2 state_store&pm_suspend 3.3 enter_state 3.3.1 valid_state 3.3.2 suspend_prepare 3.3.3 suspend_devices_and_enter 3.3.4 dpm_suspend…
阅读更多...
基于ssm框架的高校班级管理系统设计与实现

基于ssm框架的高校班级管理系统设计与实现

为解决当前高校班级管理中管理方式落后、手段落后及效率低下等问题而以当前主流的互联网技术设计一款高校班级管理系统。该系统采用B/S模式的设计思路而将前端&#xff08;JSP技术&#xff09;和后端&#xff08;SSM框架MySQL数据库&#xff09;整合于一体并通过Java语言代码编…
阅读更多...
可视化 RAG 数据 — EDA for Retrieval-Augmented Generation

可视化 RAG 数据 — EDA for Retrieval-Augmented Generation

目录 一、说明 二、准备好 三、准备文件 四、拆分和创建数据集的嵌入 五、构建 LangChain 六、问一个问题 七、可视化 八、下一步是什么&#xff1f; 九、引用 一、说明 像 GPT-4 这样的大型语言模型 &#xff08;LLM&#xff09; 在文本理解和生成方面表现出令人印象深刻的能力…
阅读更多...
fpga_直方图均衡

fpga_直方图均衡

直方图均衡是一种用于图像增强和对比度调整的图像处理技术。它通过重新分配图像中像素的灰度级分布&#xff0c;使得图像的直方图变得更加均衡&#xff0c;从而增强图像的视觉效果。 一 直方图 直方图源于柱状图 二 数字图像与灰度直方图 如图所示&#xff0c;灰度直方图是读…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023