Python 实现 ATR 指标计算(真实波幅):股票技术分析的利器系列(10)
- 介绍
- 算法解释
- 代码
- rolling函数介绍
- 核心代码
- 完整代码
介绍
ATR(真实波幅)是一种技术指标,用于衡量市场波动性的程度
| 优点 | 缺点 |
|---|---|
| 提供波动性度量,有助于风险管理和交易决策 | ATR本身不提供买卖信号,需要结合其他指标使用 |
| 简单易懂,计算方法清晰 | 对于极端行情,ATR可能无法准确反映实际波动 |
| 可适用于不同市场和时间周期 | 信号滞后,因为ATR是基于历史数据计算的 |
| 可以帮助设定止损和止盈水平 | |
| 可以作为确定交易仓位大小的参考 |
先看看官方介绍:
ATR(真实波幅)
用法
今日振幅、今日最高与昨收差价、今日最低与昨收差价中的最大值,为真实波幅,求真实波幅的N日移动平均
参数:N为天数,一般取14
算法解释
MTR:MAX(MAX((HIGH-LOW),ABS(REF(CLOSE,1)-HIGH)),ABS(REF(CLOSE,1)-LOW));
ATR:MA(MTR,N);
-
Mean True Range (MTR):
MTR代表的是平均真实波幅,它是真实波幅(TR)的移动平均值。TR是用来度量单个交易周期内的价格波动性的指标,其计算方法是当日最高价和最低价之间的差值,当日最高价和前一个交易日的收盘价之间的差值,以及当日最低价和前一个交易日的收盘价之间的差值中的最大值。MTR通过对TR进行移动平均来平滑价格波动性的波动,因此提供了更稳定的参考。
-
Average True Range (ATR):
ATR也是用来衡量价格波动性的指标,但它直接计算了一段时间内的平均波幅。与MTR不同,ATR并没有对真实波幅进行平均化处理,而是直接计算了一定时期内的TR的平均值。ATR通常用于确定价格波动性的程度,例如,较大的ATR值表示市场波动较大,而较小的ATR值表示市场波动较小。
代码
rolling函数介绍
rolling 函数通常与其他函数(如 mean、sum、std 等)一起使用,以计算滚动统计量,例如滚动均值、滚动总和等。
以下是 rolling 函数的基本语法:
DataFrame.rolling(window, min_periods=None, center=False, win_type=None, on=None, axis=0, closed=None)
window: 用于计算统计量的窗口大小。min_periods: 每个窗口最少需要的非空观测值数量。center: 确定窗口是否居中,默认为False。win_type: 窗口类型,例如None、boxcar、triang等,默认为None。on: 在数据帧中执行滚动操作的列,默认为None,表示对整个数据帧执行操作。axis: 执行滚动操作的轴,默认为0,表示按列执行操作。closed: 确定窗口的哪一端是闭合的,默认为None。
核心代码
# 计算 ATR
def calculate_atr(df, n=14):
# 计算真实范围(True Range)
df['HL'] = df['HIGH'] - df['LOW']
df['HC'] = abs(df['CLOSE'].shift(1) - df['HIGH'])
df['LC'] = abs(df['CLOSE'].shift(1) - df['LOW'])
df['MTR'] = df[['HL', 'HC', 'LC']].max(axis=1)
# 计算ATR
df['ATR'] = df['MTR'].rolling(window=n).mean()
return df.drop(['HL', 'HC', 'LC'], axis=1)
df['HL'] = df['HIGH'] - df['LOW']: 这一行计算了每个交易周期内的价格范围,即当日最高价和最低价之间的差值,结果保存在DataFrame的新列’HL’中。
df['HC'] = abs(df['CLOSE'].shift(1) - df['HIGH']): 这一行计算了当日最高价与前一个交易日收盘价之间的价差的绝对值,结果保存在DataFrame的新列’HC’中。shift(1)函数将CLOSE列向上偏移一个位置,以便与前一个交易日的CLOSE值进行计算。
df['LC'] = abs(df['CLOSE'].shift(1) - df['LOW']): 这一行计算了当日最低价与前一个交易日收盘价之间的价差的绝对值,结果保存在DataFrame的新列’LC’中。
df['MTR'] = df[['HL', 'HC', 'LC']].max(axis=1): 这一行计算了每个交易周期内的真实范围(Mean True Range)。它取了之前计算的’HL’、'HC’和’LC’列的最大值,结果保存在DataFrame的新列’MTR’中。max(axis=1)表示沿着每一行取最大值。
df['ATR'] = df['MTR'].rolling(window=n).mean(): 这一行计算了ATR(Average True Range)。它对MTR列进行滚动平均,使用了窗口大小为’n’的移动窗口。结果保存在DataFrame的新列’ATR’中。这里假设变量’n’已经在代码中定义并赋值。
完整代码
import pandas as pd
import a_get_data
# 计算 ATR
def calculate_atr(df, n=14):
# 计算真实范围(True Range)
df['HL'] = df['HIGH'] - df['LOW']
df['HC'] = abs(df['CLOSE'].shift(1) - df['HIGH'])
df['LC'] = abs(df['CLOSE'].shift(1) - df['LOW'])
df['MTR'] = df[['HL', 'HC', 'LC']].max(axis=1)
# 计算ATR
df['ATR'] = df['MTR'].rolling(window=n).mean()
return df.drop(['HL', 'HC', 'LC'], axis=1)
data = {
'CLOSE': 填每日收盘的数据,
'HIGH': 填每日最高的数据,
'LOW': 填每日最低的数据
'OPEN': 填每日开盘的数据
}
df = pd.DataFrame(data)
# 计算ATR
df = calculate_atr(df)
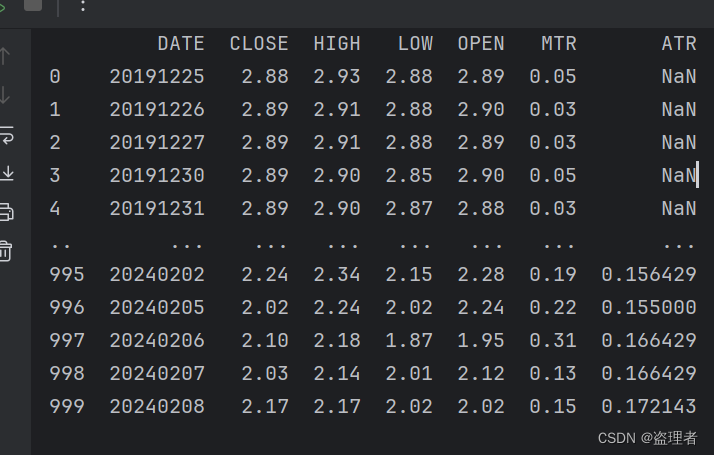
print(df)