创建时间:2024-02-19
最后编辑时间:2024-02-23
作者:Geeker_LStar
你好呀~这里是 Geeker_LStar 的人工智能学习专栏,很高兴遇见你~
我是 Geeker_LStar,一名初三学生,热爱计算机和数学,我们一起加油~!
⭐(●’◡’●) ⭐
那就让我们开始吧!
十天前,我写过本篇的姐妹篇:【初中生讲机器学习】6. 分类算法中常用的模型评价指标有哪些?here!,那既然讲完了分类算法,回归算法也是必须要讲的啦~!而且正好上一篇在讲线性回归,这一篇就接上啦。
文章目录
- R 方
- 调整后 R 方
- 均方误差 MSE
- 均方根误差 RMSE
- 平均绝对误差 MAE
- AIC 值
- BIC 值
R 方
R 方,英文全称 coefficient of determination,中文译为决定系数,是衡量回归模型性能的常用指标。
先把 R 方的公式放在这里,至于这个公式究竟是什么意思,能够反映什么,下面会分析。
R
2
=
1
−
∑
i
=
1
n
(
y
i
−
y
ˆ
i
)
2
∑
i
=
1
n
(
y
i
−
y
‾
)
2
R^2 = 1-\frac{\sum^n_{i=1}(y_i-\^y_i)^2}{\sum^n_{i=1}(y_i-\overline y)^2}
R2=1−∑i=1n(yi−y)2∑i=1n(yi−yˆi)2
先来看一个例子,比如房价,下图中黑色的水平线为房价的平均值,蓝色的竖线为某房子(变量)的价格与平均价格的差。
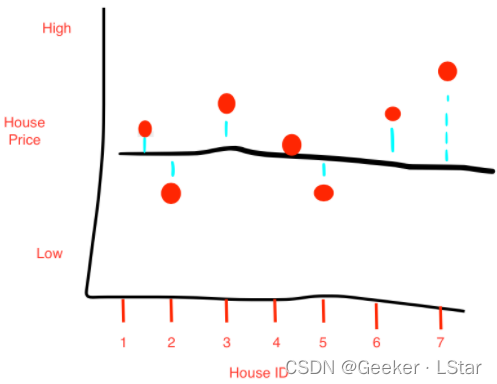
根据方差的定义(这曾在上一篇提到),这 n 组数据(房价)的方差就是:
方差
=
∑
i
=
1
n
(
第
i
个房子的价格
−
n
个房子的均价
)
2
方差 = \sum_{i=1}^n(第 i 个房子的价格-n个房子的均价)^2
方差=i=1∑n(第i个房子的价格−n个房子的均价)2这就是 R 方式子中分数部分的分母,即
∑
i
=
1
n
(
y
i
−
y
‾
)
2
\sum^n_{i=1}(y_i-\overline y)^2
∑i=1n(yi−y)2。
上面这种情况可以看做什么呢?没错,从线性回归的视角出发,这种情况就相当于我们找直线 y = 方差 y=方差 y=方差 作为回归线时,我们获得的残差平方和。
但是,在实际情况中我们肯定不能直接用方差线作为回归线,那偏差可太大了,
我们需要训练得到一个线性回归方程。比如说,我们获得的回归线是图中绿色直线这样的(所有数据已经经过排序),其中,竖直的橙色线表示残差。
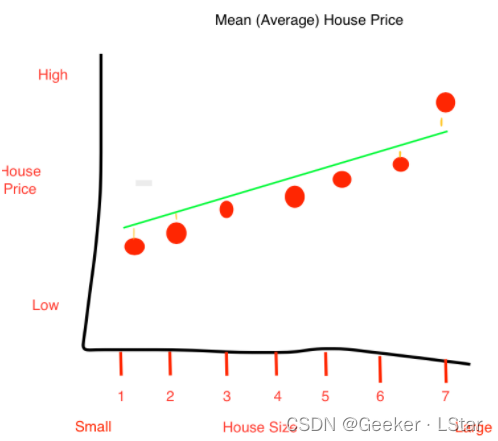
很明显,这些点到绿色线的残差平方和肯定比到方差线的残差平方和小,而这个残差平方和可以表示为 ∑ i = 1 n ( y i − y ˆ i ) 2 \sum^n_{i=1}(y_i-\^y_i)^2 ∑i=1n(yi−yˆi)2,也即 R 方式子中分数部分的分子。
其实到这里,R 方的意义已经比较明晰了,分数部分表示预测线情况下的残差平方和是方差线情况下的残差平方和的百分之几,而整个式子是 R 2 = 1 − ∑ i = 1 n ( y i − y ˆ i ) 2 ∑ i = 1 n ( y i − y ‾ ) 2 R^2 = 1-\frac{\sum^n_{i=1}(y_i-\^y_i)^2}{\sum^n_{i=1}(y_i-\overline y)^2} R2=1−∑i=1n(yi−y)2∑i=1n(yi−yˆi)2,其中 1 可以看作 100%,那用 100% 减去分数部分,相当于:和方差线情况相比,预测线情况下的残差平方和减少了百分之多少。
不过这还是不够深刻,嗯,再来看一张图。图中已经标注了 “该点的全部信息”、“未拟合出的信息” 和 “拟合出的信息”。水平红色虚线代表方差线,倾斜黑色虚线代表拟合出的回归线。
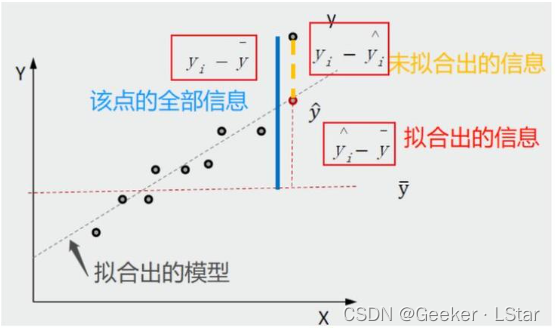
其中,“该点的全部信息” 构成总平方和(SST),即 ∑ i = 1 n ( y i − y ‾ ) 2 \sum^n_{i=1}(y_i-\overline y)^2 ∑i=1n(yi−y)2,也就是方差。“拟合出的信息” 被称为 SSR,这部分通常是由自变量引起的,可以用回归线解释,即 ∑ i = 1 n ( y ˆ i − y ‾ ) 2 \sum^n_{i=1}(\^y_i-\overline y)^2 ∑i=1n(yˆi−y)2。剩下的 “未拟合出的信息” 被称为残差,构成残差平方和(SSE),这部分通常不是由自变量而是由随机扰动项引起的,不能用回归线解释,即 ∑ i = 1 n ( y i − y ˆ i ) 2 \sum^n_{i=1}(y_i-\^y_i)^2 ∑i=1n(yi−yˆi)2。
容易看出,
S
S
T
=
S
S
R
+
S
S
E
,
S
S
E
=
S
S
T
−
S
S
R
,即
∑
i
=
1
n
(
y
i
−
y
ˆ
i
)
2
=
∑
i
=
1
n
(
y
i
−
y
‾
)
2
−
∑
i
=
1
n
(
y
ˆ
i
−
y
‾
)
2
SST = SSR+SSE,SSE = SST-SSR,即 \sum^n_{i=1}(y_i-\^y_i)^2 = \sum^n_{i=1}(y_i-\overline y)^2 - \sum^n_{i=1}(\^y_i-\overline y)^2
SST=SSR+SSE,SSE=SST−SSR,即∑i=1n(yi−yˆi)2=∑i=1n(yi−y)2−∑i=1n(yˆi−y)2。对于大多数回归模型而言,肯定是 “由自变量引起、可以用回归线解释” 的部分的占比越大越好,也就是 SSR 占 SST 的比例越大越好。换言之,我们需要让下面这个式子最大:
S
S
R
S
S
T
=
∑
i
=
1
n
(
y
ˆ
i
−
y
‾
)
2
∑
i
=
1
n
(
y
i
−
y
‾
)
2
=
1
−
S
S
E
S
S
T
=
1
−
∑
i
=
1
n
(
y
i
−
y
ˆ
i
)
2
∑
i
=
1
n
(
y
i
−
y
‾
)
2
\frac{SSR}{SST} = \frac{\sum^n_{i=1}(\^y_i-\overline y)^2}{\sum^n_{i=1}(y_i-\overline y)^2} = 1-\frac{SSE}{SST} = 1-\frac{\sum^n_{i=1}(y_i-\^y_i)^2}{\sum^n_{i=1}(y_i-\overline y)^2}
SSTSSR=∑i=1n(yi−y)2∑i=1n(yˆi−y)2=1−SSTSSE=1−∑i=1n(yi−y)2∑i=1n(yi−yˆi)2
看到没()这个式子不就是 R 方表达式嘛!
so,R 方表示什么,表示的是,在方差中,由自变量引起,且可以用回归线解释的部分的占比。 那这就明确了,R 方肯定是越接近于 1 越好呀,如果 R 方等于 1,那就相当于模型解释了所有的方差,即对全部数据的拟合(预测)都完全准确,和真实值完全相同。
这是不同 R 方情况对应的模型的表现。R 方等于 0 对应着直接把数据的平均值作为预测值(方差线),R 方等于 1 是最好的情况,其它情况介于两者之间。
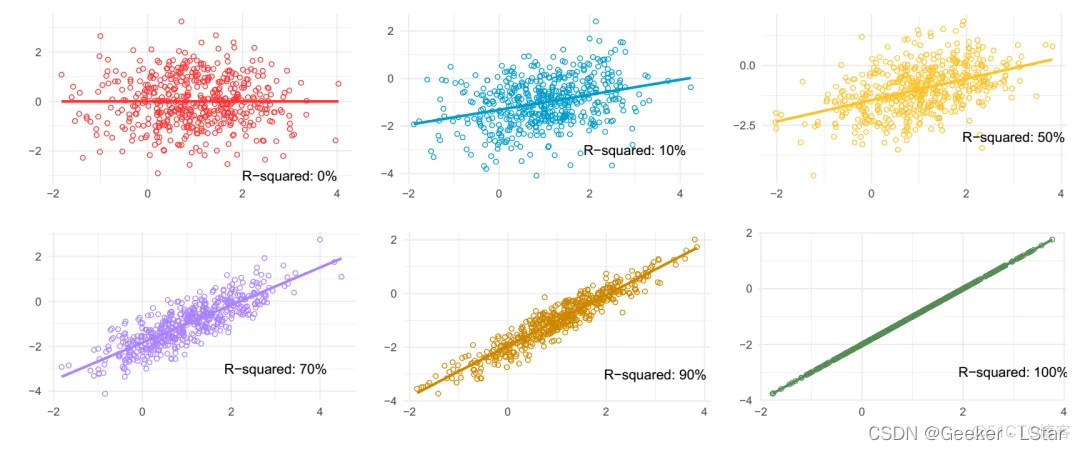
ok,还有一个比较容易弄混的问题,就是 R 方的范围到底是多少,有些人说是
(
−
∞
,
1
]
(-∞, 1]
(−∞,1],也有些人说是
[
0
,
1
]
[0,1]
[0,1],这其实取决于我们在什么限定条件下,换言之,这取决于我们是否固定截距项。
什么意思呢?for example,我们的回归方程是
y
=
a
x
+
b
y = ax+b
y=ax+b,如果固定了截距项 b,像下图这种情况,那这时候的 R 方就会出现负数了,下面这个例子中 R 方就是负数。
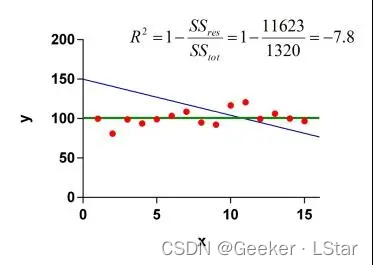
不过,固定截距项一般没什么意义,在线性回归中也很少这么用(在上一篇的推导中说过,最小二乘法不固定截距项),所以在线性回归中,R 方的范围是 [ 0 , 1 ] [0,1] [0,1],和我们通常的认知是一样的。
so,R 方怎么计算?没错,sklearn 封装好函数了~(自己封装也可以,算法很简单)。以下是完整代码:
# 导入库
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import r2_score
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 自制数据 + 绘图查看数据分布
np.random.seed(218)
x = np.random.uniform(-3.0, 3.0, size=3000)
X = x.reshape(-1, 1)
y = 2.18 * x + 2 + np.random.normal(0, 2, size=3000)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=218)
plt.scatter(X, y)
plt.show()
# 训练 & 测试
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_predict = lin_reg.predict(X_test)
r2 = r2_score(y_test, y_predict)
print(r2)
回归算法不能再用我们熟悉的鸢尾花数据集了,so 我在这里自己造了 3000 组数据(不得不说 numpy 真的好用),然后用线性回归拟合,最后训练 & 测试就 ok。数据的分布如下图:
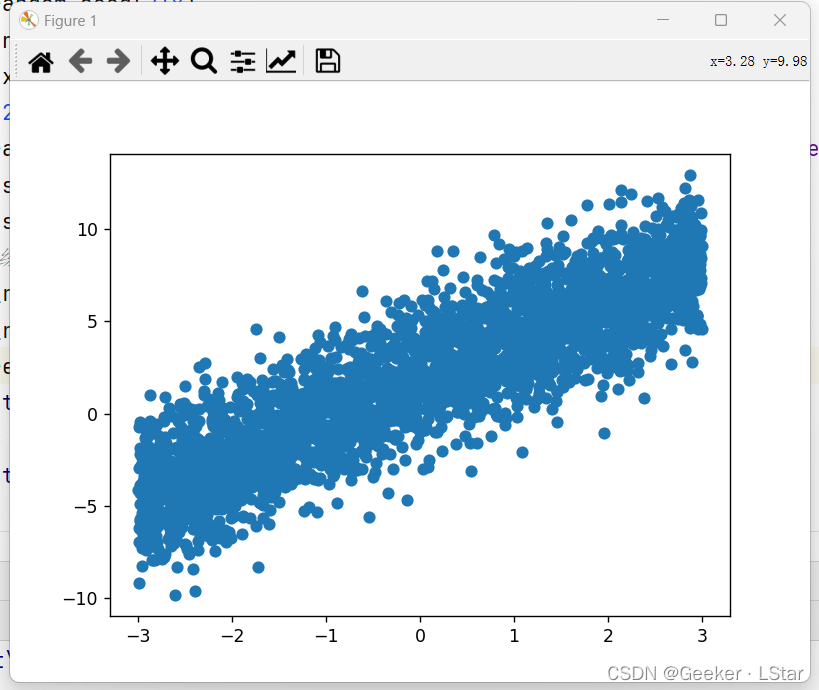
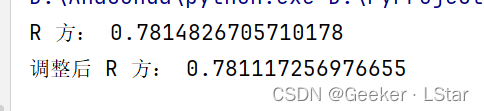
R 方的结果是 0.78 左右,还可以吧~
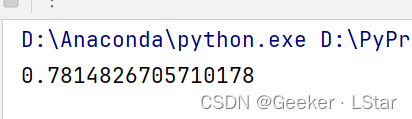
嗯,我想上述对于 R 方的解释已经比较清晰了。R 方确实是个很常用的指标,但它同时也有一些缺陷。
调整后 R 方
一句话:调整后 R 方避免了自变量个数增加对指标值的影响,有利于挑选出对预测因变量真正有用的自变量,能够减少过拟合,提高模型的泛化能力。
普通 R 方的缺陷在于,它衡量的是 “自变量对因变量方差的解释程度”,但是,在我们大量增加自变量数量的时候,哪怕我们增加的是一些不那么重要的自变量,R 方也会只增不减,也就是说,在我们增加自变量的时候,R 方会带给我们一种 “模型性能变得越来越好” 的错觉,但实际上,这可能只是过拟合的结果。也就是说,R 方的减小并不代表模型的性能提升了多少,而(可能)是自变量过多造成了过拟合。
这可不是我们想要的。so,我们引入了调整后 R 方,对自变量的数量进行了一波制约。
嗯,至于为什么 “自变量增加,R 方一定增加”,证明在下面~

so,调整后 R 方是怎么做的呢?先来看它的式子:
A
d
j
u
s
t
e
d
R
−
s
q
u
a
r
e
d
=
1
−
(
1
−
R
2
)
n
−
1
n
−
k
−
1
Adjusted R-squared = 1-(1-R^2)\frac{n-1}{n-k-1}
AdjustedR−squared=1−(1−R2)n−k−1n−1先不说自由度这样的概念,简单来看,n 就是样本数(训练集大小),k 就是要预测的回归系数的个数,分母中的 “-1” 是因为我们还有一个截距项 b,也是需要预测的(但是一般不把它叫做系数,so 就单独提出来了)。
那么,如果我们添加了大量没什么用的变量,R 方的确会升高,但是在调整后 R 方这里,情况发生了变化:没用的变量数量增加,n-k-1 的值(即分母的值)减小,
n
−
1
n
−
k
−
1
\frac{n-1}{n-k-1}
n−k−1n−1 的值增大,导致调整后 R 方下降。相当于一个惩罚项吧,调整后 R 方相当于让我们 “用最少的自变量达到最优的预测效果”。
也就是说,调整后 R 方能够帮我们选出对预测因变量真正有用的自变量,这有利于我们剔除无用的自变量,减少过拟合,提升模型的泛化能力。
好ok,前面提到自由度的概念,这里浅说一下。
自由度,英文 degrees of freedom,简写为 DF。在统计学上的标准定义是:在计算某一统计量时,取值不受限制的变量个数。自由度可以帮助我们了解系统的复杂性和可预测性。
式子
1
−
(
1
−
R
2
)
n
−
1
n
−
k
−
1
1-(1-R^2)\frac{n-1}{n-k-1}
1−(1−R2)n−k−1n−1 中的
n
−
1
n-1
n−1 和
n
−
k
−
1
n-k-1
n−k−1 是什么呢?
yes 没错,这俩就是自由度,第一个是总自由度,第二个是残差(或者说误差)自由度。这两个自由度是线性回归中最常用的两个。
总自由度(DFtot),计算公式
n
−
1
n-1
n−1,其中 n 为样本量(训练集大小),1 为因变量个数。一般来说,总自由度越大,说明用于训练的样本越多,模型的性能一般来讲会更好。
残差自由度(DFres),计算公式
n
−
k
−
1
n-k-1
n−k−1,其中 n 为样本量(训练集大小),k 为回归系数的个数,1 代表截距项 b。一般来讲,残差自由度如果比总自由度小很多,说明自变量的个数可能太多了(添加了一些无关自变量),容易导致过拟合,此时就需要我们找到并剔除一些无关自变量了。
自由度的概念很复杂,在这里不过多展开了。总而言之,在机器学习中,自由度可以帮我们衡量模型的训练程度。在一定范围内,自由度高,说明模型训练的比较充分,但是如果自由度过高(或残差自由度和总自由度的差异过大),则需要考虑模型是否过拟合。
关于自由度的更多内容,可以参考这篇:How to Calculate the Degrees of Freedom。
我们说回调整后 R 方。
一般而言,调整后 R 方比 R 方更 “客观” 一些,多元线性回归中,为了保证挑选的自变量都是有用的,通常使用调整后 R 方而不是 R 方作为检验指标。调整后 R 方大于 0.5,说明模型性能过关,小于 0.5 则说明模型性能不太好。
同时,如果 R 方和调整后 R 方相差过大(R 方比调整 R 方大太多),说明模型过拟合了,性能不佳。
说了这么多理论,在 Python 中,调整后 R 方要怎么计算呢?sklearn 貌似没有相关函数,不过我们直接用计算出的 R 方再套一下公式就 ok 了其实~(当然,自己封装一个函数肯定是可以的,R 方和调整 R 方的计算都不难),代码如下:
(是接着上面 R 方的代码写的)
# 计算调整后 R 方
n = 600 # 测试样本量
k = 1 # 回归系数个数
adjusted_r2 = 1-((1-r2)*(n-1)/(n-k-1))
print("调整后 R 方:", adjusted_r2)
调整后 R 方也差不多是 0.78,和 R 方非常接近,说明这个模型几乎没有过拟合(也是,这就一个变量它上哪里过拟合去,,,)。
好好好,把难度降下来()这两个的确有点不好理解emm尤其是那个抽象自由度,我查了半天。
不过从下面开始就简单了。
均方误差 MSE
均方误差,英文全称 mean square error,简称 MSE。
均方误差是 “平均平方误差” 的简称,对于每一个样本,我们只需把它的预测值和真实值做差后再平方,并把 n 个样本的结果加起来之后再乘 1/n 即可,说白了就是残差平方和的平均数。计算公式:
M
S
E
=
1
n
∑
i
=
1
n
(
y
^
i
−
y
)
2
MSE = \frac{1}{n}\sum_{i=1}^{n}(\hat y_i-y)^2
MSE=n1i=1∑n(y^i−y)2
yes,这个公式你可能很熟悉,我们在上一篇中用最小二乘法求解回归系数的时候用的就是类似的公式,没有乘 1/n 而已。
均方误差用起来简单,但是它用了平方,所以容易受到离群值(极端值)的影响,并且和 R 方一样,大量的无关自变量可能会使均方误差降低,模型的性能看似提高了,但这只是过拟合的结果。
sklearn 提供了计算均方误差的方法,很简单:
# 计算均方误差
mse = mean_squared_error(y_test, y_predict)
print(mse)
均方根误差 RMSE
均方根误差,英文全称 root mean square error,简称 RMSE。
其实从它的名字我们已经很能知道它的计算方法了——把 MSE 开平方即可。
R
M
S
E
=
1
n
∑
i
=
1
n
(
y
^
i
−
y
)
2
RMSE = \sqrt{\frac{1}{n}\sum_{i=1}^{n}(\hat y_i-y)^2}
RMSE=n1i=1∑n(y^i−y)2
和 MSE 一样,均方根误差容易受到离群值影响,同时不太能检验出自变量是否对预测因变量有贡献。
通常来讲,RMSE 比 MSE 更常用。
# 计算均方根误差
rmse = np.sqrt(mse)
print(rmse)
平均绝对误差 MAE
平均绝对误差,英文全称 mean absolute error,简称 MAE。
MAE 和前面两个的套路类似,但是它把平方换成了绝对值。
M
A
E
=
1
n
∑
i
=
1
n
∣
y
^
i
−
y
∣
MAE = \frac{1}{n}\sum_{i=1}^{n}|\hat y_i-y|
MAE=n1i=1∑n∣y^i−y∣
MAE 相较于前两个,不那么受离群值的影响,但是它也不太能判断自变量是否对预测因变量有贡献。
# 计算平均绝对误差
mae = mean_absolute_error(y_test, y_predict)
print(mae)
ok,中场休息了一下,下面继续开始上难度。。。。
首先,我们需要理解一件重要的事情,我把它称作——机器学习的主要矛盾(不是(doge))。
我们来考虑这样一件事:如果我们想提高模型的性能,可以多选择一些自变量(注意,不是训练数据,而是自变量),让它学习得更为充分一些,捕捉到更多的特征,进而表现出更好的结果。但是,如果我们选择的自变量过多,容易造成过拟合,模型的性能反而会下降。
也就是说,模型的复杂度和精度(拟合程度)之间存在一个 “微妙的平衡”,如果把握不好这个平衡,而只是一味升高或降低模型的复杂度,都会导致模型的精度不佳。
模型的复杂度和精度(拟合程度)之间的关系可以用下图来表示:
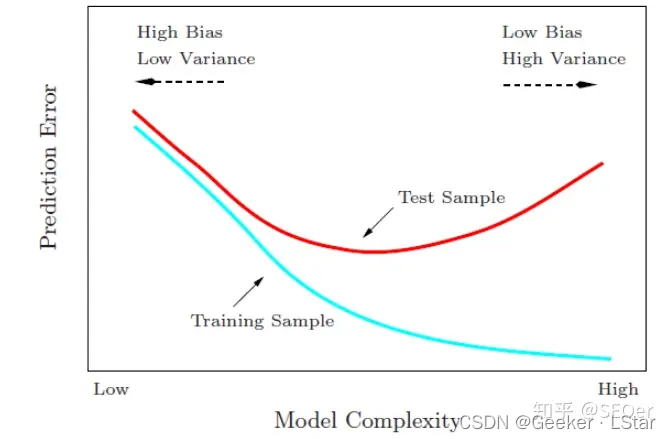
那么,这个“平衡点”怎么找呢?yesyes,AIC 值和 BIC 来帮我们啦!
一句话概括:AIC/BIC = 模型复杂度 - 模型精度。
AIC 值
AIC 值,英文全称 Akaike information criterion,翻译为赤池信息准则,它可以帮助我们在复杂度和精度之间寻找平衡,选出最优模型。
上一篇中我讲过,线性回归的实质就是 “最小化残差平方和”,而 AIC 在此基础之上增加了一项——模型参数的数量。AIC 会 “惩罚” 那些自变量数量过多的模型,以减少过拟合的发生。一般来讲,我们会选择 AIC 值最小的模型。
让我们来看看 AIC 的公式:
A
I
C
=
2
k
−
2
l
n
(
L
)
AIC = 2k-2ln(L)
AIC=2k−2ln(L)其中,k 是模型的参数(自变量)数量,L 是模型的似然函数。
ok 先来讲讲这个似然函数。这个东西其实蛮值得好好讲讲的,so 我计划单开一篇,这里先简单说一下吧。
“概率” 是指,在前提条件 A 下,发生 B 的可能性是多少,即 P(B|A)。而 “似然” 与之相反,它表示在已经发生 B 的情况下,前提条件 A 成立的可能性是多少,即 P(A|B),也就是 P(B|A) 的逆概率。
如果你看过 【初中生讲机器学习】5. 从概率到朴素贝叶斯算法,一篇带你看明白!这篇,你会很快明白上面那几行的意思,用贝叶斯公式来推的话其实就是
P
(
A
∣
B
)
=
P
(
B
∣
A
)
P
(
A
)
P
(
B
)
P(A|B) = \frac{P(B|A)P(A)}{P(B)}
P(A∣B)=P(B)P(B∣A)P(A),也就是后验概率。
不过这里的 “似然函数” 并不需要像上面的贝叶斯公式那样算出具体的数值(当然如果你要算也可以,只不过没有必要啦~),它衡量的只是 “参数对于样本的适应性”。换言之,似然函数越大,说明在当前的数据样本条件下,模型的拟合越好。我们不用关注似然函数的具体值,只需要看在改变参数时,似然函数是变大还是变小就 ok 了。
那么,此时 AIC 值的计算公式就变了好理解了。公式:
A
I
C
=
2
k
−
2
l
n
(
L
)
AIC = 2k-2ln(L)
AIC=2k−2ln(L),ln(L) 是似然函数的对数,衡量的是模型的拟合程度,拟合程度越好,该项越大;k 是自变量(参数)的数量,衡量的是模型的复杂度,自变量越少,该项越小。 k 项相当于一个惩罚项,如果自变量太多,k 变大,则 AIC 值也会变大。
一个预测能力强的模型应该是 “L 大” & “k 小” 这样的组合,对应的是 AIC 值最小的组合。
emm,这次 sklearn 没办法了,不过 statsmodels 库给我们提供了计算 AIC 值的方法,还是相对简单的。
from statsmodels.regression.linear_model import OLS
from statsmodels.tools import add_constant
# 计算 AIC 值——库
reg = OLS(y_test, add_constant(X_test)).fit()
print("AIC 值:", reg.aic)
当然,我们也可以手搓一个(坏笑),比如:
(关于为什么这么算,我打算在讲似然的时候再详细说~)
# 计算 AIC 值——手搓版
k = 2 # 一个回归系数和一个截距项
def llf_(ytest, Xtest, ypredict):
# 返回最大对数似然
nobs = float(Xtest.shape[0])
nobs2 = nobs / 2.0
residual = ytest - ypredict
ssr = np.sum((residual)**2) # 残差平方和
llf = -nobs2*np.log(2*np.pi) - nobs2*np.log(ssr/nobs) - nobs2 # 最大对数似然
return llf
# 计算 AIC 值
def aic(y, X, predict, k):
# 返回 AIC 值
llf = llf_(y, X, predict)
return -2*llf + 2*k
aic2 = aic(y_test, X_test, y_predict, k)
print("手搓版 AIC 值:", aic2)
看一下结果,我们的计算公式是正确的~!至于那微小的差别,估计是 statsmodels 库和 sklearn 库内置的 fit() 函数不完全相同导致的。

BIC 值
BIC 值,英文全称 Bayesian information criterion,翻译为 “贝叶斯信息准则”,看名字就知道,它和 AIC 值的作用很相似——寻找模型复杂度和精度(拟合程度)之间的平衡,帮我们选则预测能力最强的模型。
BIC 值的计算公式:
B
I
C
=
k
l
n
(
n
)
−
2
l
n
(
L
)
BIC = kln(n)-2ln(L)
BIC=kln(n)−2ln(L)后半部分和 AIC 一样,衡量的是模型的精度(拟合程度),不再说了,重点来看一下前半部分。
前半部分中,k 依然是自变量(参数)的数量,而 n 是训练样本的数量。在 k 值较大的时候,BIC 的 “惩罚” 会比 AIC 更重,也就是说相比于 AIC,BIC 对模型的 “简单” 要求更为严格,BIC 选出的模型的参数数量可能会比 AIC 更少。
它们两个的计算原理还是比较相似的(至少从公式看来),代码不再重复改了,可以参考 AIC 的~
放一下总体代码吧~
# 回归模型中常用的评价指标
# R 方、调整后 R 方、均方误差、均方根误差、平均绝对误差、AIC 值、BIC 值
# 导入库
from statsmodels.regression.linear_model import OLS
from statsmodels.tools import add_constant
import matplotlib.pyplot as plt
import numpy as np
from sklearn.metrics import r2_score, mean_squared_error, mean_absolute_error
from sklearn.linear_model import LinearRegression
from sklearn.model_selection import train_test_split
# 自制数据 + 绘图查看数据分布
np.random.seed(218)
x = np.random.uniform(-3.0, 3.0, size=3000)
X = x.reshape(-1, 1)
y = 2.18 * x + 2 + np.random.normal(0, 2, size=3000)
X_train, X_test, y_train, y_test = train_test_split(X, y, test_size=0.2, random_state=218)
plt.scatter(X, y)
plt.show()
# 训练 & 测试
lin_reg = LinearRegression()
lin_reg.fit(X_train, y_train)
y_predict = lin_reg.predict(X_test)
# 计算 R 方
r2 = r2_score(y_test, y_predict)
print("R 方:", r2)
# 计算调整后 R 方
n = 600 # 测试样本量
k = 1 # 回归系数个数
adjusted_r2 = 1-((1-r2)*(n-1)/(n-k-1))
print("调整后 R 方:", adjusted_r2)
# 计算均方误差
mse = mean_squared_error(y_test, y_predict)
print("均方误差:", mse)
# 计算均方根误差
rmse = np.sqrt(mse)
print("均方根误差:", rmse)
# 计算平均绝对误差
mae = mean_absolute_error(y_test, y_predict)
print("平均绝对误差:", mae)
# 计算 AIC 值——库(计算出的是最理想的情况)
reg = OLS(y_test, add_constant(X_test)).fit()
print("AIC 值:", reg.aic)
# 计算 AIC 值——手搓版
k = 2 # 一个回归系数和一个截距项
def llf_(ytest, Xtest, ypredict):
# 返回最大对数似然
nobs = float(Xtest.shape[0]) # 测试集大小
nobs2 = nobs / 2.0
residual = ytest - ypredict
ssr = np.sum((residual)**2) # 残差平方和
llf = -nobs2*np.log(2*np.pi) - nobs2*np.log(ssr/nobs) - nobs2 # 最大对数似然
return llf
# 计算 AIC 值
def aic(y, X, predict, k):
# 返回 AIC 值
llf = llf_(y, X, predict)
return -2*llf + 2*k
aic2 = aic(y_test, X_test, y_predict, k)
print("手搓版 AIC 值:", aic2)
最终结果:

ok!!以上就是关于回归算法中常用的模型评价指标的详细讲解!!
这篇文章讲了回归算法中常用的模型评价指标,并给出了对应的代码,希望对你有所帮助!⭐
——Geeker_LStar