Floyd算法详解

news2024/10/7 14:21:37

这里是引用

文章目录

  • 写在前面
  • 要说floyd就不能只说板子
    • 状态
    • 转移
    • 空间优化
    • kij or ijk
  • 应用
    • 求多源最短路
    • 求传递闭包
    • 求无向图的最小环

写在前面

在做洛谷的树上dp题单的时候遇到了一道题目P1613 跑路发现自己对flyod的理解太浅薄了，于是去重新学习了一遍，又做了几道题目，然后结合了acwing的算法提高课的总结，于是乎有了这篇博客。

要说floyd就不能只说板子

什么是floyd，提到floyd肯定就会想到最短路。

Floyd算法又称为插点法，是一种利用动态规划的思想寻找给定的加权图中多源点之间最短路径的算法，与Dijkstra算法类似。该算法名称以创始人之一、1978年图灵奖获得者、斯坦福大学计算机科学系教授罗伯特·弗洛伊德命名。

我们现在看到的形式

for(int k=1;k<=n;k++){
	for(int i=1;i<=n;++j){
		for(int k=1;k<=n;++k){
			d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
		}
	}
}

现在我们的板子中经常看到的floyd都是二维，其实最原始的状态是三维。

状态

d [ k ] [ i ] [ j ] d[k][i][j] d[k][i][j]:从 i i i点到 j j j点只经过，前k个结点 （ 1 、 2 、 3 、 . . . 、 k − 1 、 k ） （1、2、3、...、k-1、k） （1、2、3、...、k−1、k）的最短距离

转移

转移的时候是以经不经过第 k k k个结点来划分进行转移的。
不经过：
d [ k ] [ i ] [ j ] = d [ k − 1 ] [ i ] [ j ] d[k][i][j]=d[k-1][i][j] d[k][i][j]=d[k−1][i][j]
经过：
d [ k ] [ i ] [ j ] = d [ k − 1 ] [ i ] [ k ] + d [ k − 1 ] [ j ] [ k ] d[k][i][j]=d[k-1][i][k]+d[k-1][j][k] d[k][i][j]=d[k−1][i][k]+d[k−1][j][k]
所以状态转移方程为：
d [ k ] [ i ] [ j ] = m i n ( d [ k − 1 ] [ i ] [ j ] , d [ k − 1 ] [ i ] [ k ] + d [ k − 1 ] [ j ] [ k ] ) d[k][i][j]=min(d[k-1][i][j],d[k-1][i][k]+d[k-1][j][k]) d[k][i][j]=min(d[k−1][i][j],d[k−1][i][k]+d[k−1][j][k])

空间优化

观察上面的状态转移方程可以看到在算第 k k k层的状态时，只用到了 k − 1 k-1 k−1层的状态，这就启发了我们是不是可以像背包问题那样，优化掉一维的空间。
我们可以看一下去掉第一维会不会得到的方程是否和原方程等价.
也就是说我们在去点第一维后,在算第 k k k层的d[i][j]时 d [ i ] [ k ] d[i][k] d[i][k]和 d [ j ] [ k ] d[j][k] d[j][k]中存的仍然是第 k − 1 k-1 k−1层的结果.
是不是这样呢?
要想看 d [ i ] [ k ] d[i][k] d[i][k]和 d [ j ] [ k ] d[j][k] d[j][k]中存的是不是第 k − 1 k-1 k−1层的结果.我们可以考虑 d [ i ] [ k ] d[i][k] d[i][k]和 d [ j ] [ k ] d[j][k] d[j][k]在k层时什么时候会更新
先考虑 d [ i ] [ k ] d[i][k] d[i][k]什么时候更新
d [ k ] [ i ] [ j ] = m i n ( d [ k − 1 ] [ i ] [ j ] , d [ k − 1 ] [ i ] [ k ] + d [ k − 1 ] [ j ] [ k ] ) d[k][i][j]=min(d[k-1][i][j],d[k-1][i][k]+d[k-1][j][k]) d[k][i][j]=min(d[k−1][i][j],d[k−1][i][k]+d[k−1][j][k])
当 j = k j=k j=k时显然第 k − 1 k-1 k−1层的 d [ i ] [ k ] d[i][k] d[i][k]会更新,我们把 j = k j=k j=k带入有=d[k-1][i][k]
d [ k ] [ i ] [ k ] = m i n ( d [ k − 1 ] [ i ] [ j ] , d [ k − 1 ] [ i ] [ k ] + d [ k − 1 ] [ k ] [ k ] ) d[k][i][k]=min(d[k-1][i][j],d[k-1][i][k]+d[k-1][k][k]) d[k][i][k]=min(d[k−1][i][j],d[k−1][i][k]+d[k−1][k][k])
由于 d [ k − 1 ] [ k ] [ k ] = 0 d[k-1][k][k]=0 d[k−1][k][k]=0,有
d [ k ] [ i ] [ k ] = d [ k − 1 ] [ i ] [ k ] d[k][i][k]=d[k-1][i][k] d[k][i][k]=d[k−1][i][k]
所以这是等价变形的.
然后可以考虑 i = k i=k i=k时,情况是一样的.
然后我们就可以证明这两个状态转移方程是等价的.也就有了新的状态转移方程
d [ i ] [ j ] = m i n ( d [ i ] [ j ] , d [ i ] [ k ] + d [ k ] [ j ] ) d[i][j]=min(d[i][j],d[i][k]+d[k][j]) d[i][j]=min(d[i][j],d[i][k]+d[k][j])

kij or ijk

从dp的角度考虑也就很自然的会得出循环k在在最外层.
具体的为什么在最外层知乎上已经很多回答了.可以看下面的链接
为什么是kij不是ijk

应用

求多源最短路

AcWing 1125. 牛的旅行

题意是给了一堆牧场

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define pdd pair<double,double>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define vi vector<int>


using namespace std;

int n,m;
const int N=200;
const db inf=1e20;
db d[N][N],mv[N];
pdd a[N];
char g[N][N];

void solve() {
	cin>>n;
	rep(i,1,n) {
		cin>>a[i].x>>a[i].y;
	}
	rep(i,1,n) {
		cin>>g[i]+1;
	}


	auto dist=[&](pdd a, pdd b) {
		db dx=a.x-b.x;
		db dy=a.y-b.y;
		return sqrt(dx*dx+dy*dy);
	};

	rep(i,1,n) {
		rep(j,1,n) {
			if(i==j) {
				d[i][j]=0;
			} else if(g[i][j]=='1') {
				d[i][j]=dist(a[i],a[j]);
			} else {
				d[i][j]=inf;
			}
		}
	}

	//跑一遍floyd
	rep(k,1,n) {
		rep(i,1,n) {
			rep(j,1,n) {
				d[i][j]=min(d[i][j],d[i][k]+d[k][j]);
			}
		}
	}

	//预处理出来每个点到连通块其他点的最短路的最大值
	db ans1=0,ans2=inf;

	rep(i,1,n) {
		rep(j,1,n) {
			if(d[i][j]<inf) {
				mv[i]=max(mv[i],d[i][j]);
			}
		}
		ans1=max(ans1,mv[i]);
	}
//	cout<<ans2<<endl;

	rep(i,1,n) {
		rep(j,1,n) {
			if(d[i][j]>=inf) {
				ans2=min(ans2,mv[i]+mv[j]+dist(a[i],a[j]));
			}
		}
	}
	cout<<setiosflags(ios::fixed)<<setiosflags(ios::right)<<setprecision(6)<<max(ans1,ans2)<<endl;
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}

求传递闭包

传递闭包:在有向图中，如果a->b,并且b->c那么a->c.换句话说将所有能间接到达的点都连上直接的边后的图就是原图的传递闭包

oiwiki上面用bitset进行的优化
1708700577628.png

AcWing 343. 排序

思路：
da4c44307aa5b7606ac68dada80e109.jpg
1d6a83bdcd9dbc288cb692eca7916df.jpg
时间复杂度: O ( m n 3 ) O(mn^3) O(mn3)
代码有点长

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define pdd pair<double,double>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define vi vector<int>


using namespace std;

void solve() {
	int n,m;
	
	while(cin>>n>>m,n||m){
		vector<vector<int>>g(n+1,vector<int>(n+1));
		vector<vector<int>>d(n+1,vector<int>(n+1));
		auto floyd=[&](){
			rep(k,0,n-1){
				rep(i,0,n-1){
					rep(j,0,n-1){
						d[i][j]|=d[i][k]&&d[k][j];
					}
				}
			}		
		};
		auto check=[&](){
			rep(i,0,n-1){
				if(d[i][i])	return 2;
			}
			rep(i,0,n-1){
				rep(j,0,i-1){
					if(!d[i][j]&&!d[j][i]){
						return 0;
					}
				}
			}
			return 1;
		};
		int type=0,turn=0;
		rep(i,1,m){
			string s;
			cin>>s;
			int u=s[0]-'A',v=s[2]-'A';
			if(!type){
				d[u][v]=1;
				floyd();
				type=check();
				if(type){
					turn=i;
				}
			}
		}
		if(!type){
			cout<<"Sorted sequence cannot be determined."<<endl;
		}else if(type==2){
			cout<<"Inconsistency found after "<<turn<<" relations."<<endl;
		}else{
			vector<int>st(n+1,0);
			auto getmn=[&](){
				rep(i,0,n-1){
					if(!st[i]){
						int flag=0;
						rep(j,0,n-1){
							if(!st[j]&&d[j][i]){
								flag=1;
								break;
							}
						}
						if(!flag){
							st[i]=1;
							char c='A'+i;
							return c;
						}
					}
				}
			};
			cout<<"Sorted sequence determined after "<<turn<<" relations: ";
			rep(i,0,n-1){
				cout<<getmn();
			}
			cout<<"."<<endl;
		}
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}

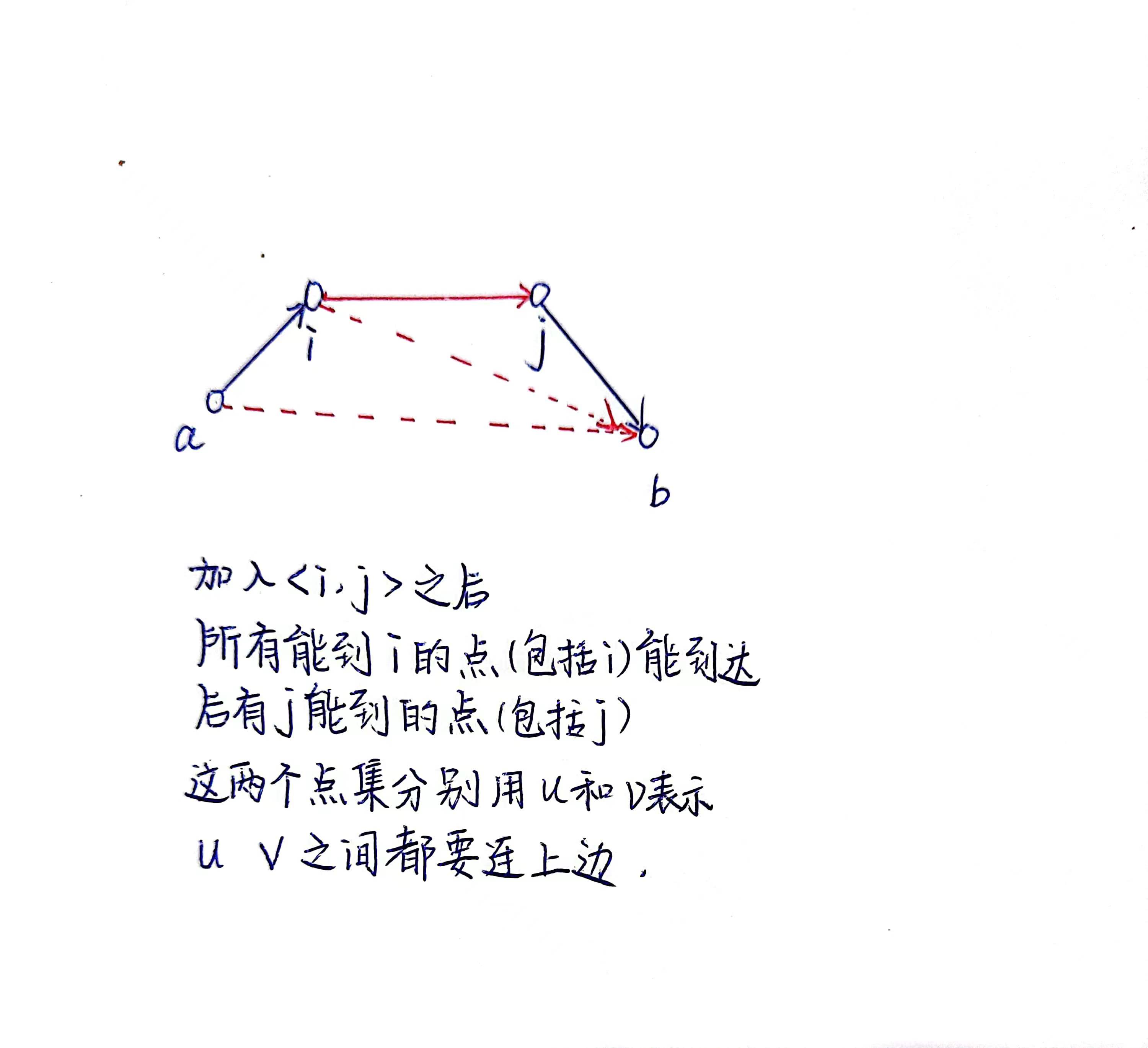
考虑加上优化

每加入一条边之后其实并不需要再重新跑一遍 f l o y d floyd floyd,我们只需要考虑这条新加入的边会产生什么影响即可。
8df63bc478d463a15c581fbb0d4c8b6.jpg
时间复杂度： O ( m n 2 ) O(mn^2) O(mn2)

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define pdd pair<double,double>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define vi vector<int>


using namespace std;

void solve() {
	int n,m;
	
	while(cin>>n>>m,n||m){
		vector<vector<int>>g(n+1,vector<int>(n+1));
		vector<vector<int>>d(n+1,vector<int>(n+1));
		auto check=[&](){
			rep(i,0,n-1){
				if(d[i][i])	return 2;
			}
			rep(i,0,n-1){
				rep(j,0,i-1){
					if(!d[i][j]&&!d[j][i]){
						return 0;
					}
				}
			}
			return 1;
		};
		
		int type=0,turn=0;
		rep(i,1,m){
			string s;
			cin>>s;
			int u=s[0]-'A',v=s[2]-'A';
			if(!type){
				d[u][v]=1;
				auto kkk=[&](){
					rep(i,0,n-1){
					    //处理能到达v能到的所有点
						if(d[v][i]) d[u][i]=1;
						//所有能到u的点都能到v
						if(d[i][u]) d[i][v]=1;
						
						//所有能到u的点不包含u
						if(d[i][u]){
							rep(j,0,n-1){
								//所有v能到的点不包含v
								if(d[v][j]){
									d[i][j]=1;
								}
							}
						}
					}
				};
				kkk();
				type=check();
				if(type){
					turn=i;
				}
			}
		}
		if(!type){
			cout<<"Sorted sequence cannot be determined."<<endl;
		}else if(type==2){
			cout<<"Inconsistency found after "<<turn<<" relations."<<endl;
		}else{
			vector<int>st(n+1,0);
			auto getmn=[&](){
				rep(i,0,n-1){
					if(!st[i]){
						int flag=0;
						rep(j,0,n-1){
							if(!st[j]&&d[j][i]){
								flag=1;
								break;
							}
						}
						if(!flag){
							st[i]=1;
							char c='A'+i;
							return c;
						}
					}
				}
			};
			cout<<"Sorted sequence determined after "<<turn<<" relations: ";
			rep(i,0,n-1){
				cout<<getmn();
			}
			cout<<"."<<endl;
		}
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}

求无向图的最小环

AcWing 344. 观光之旅
oiwiki上面无向图找环说的很清楚。
1708703766532.png、
关于这道题目的一个难点是记录状态。

#include <bits/stdc++.h>
#define int long long
#define rep(i,a,b) for(int i = (a); i <= (b); ++i)
#define fep(i,a,b) for(int i = (a); i >= (b); --i)
#define pii pair<int, int>
#define pdd pair<double,double>
#define ll long long
#define db double
#define endl '\n'
#define x first
#define y second
#define pb push_back
#define vi vector<int>


using namespace std;

void solve() {
	int n,m;
	cin>>n>>m;
	//g用于存原图，因为求最小环的时候需要原图中的边长
	vector<vi>g(n+1,vi(n+1,0x3f3f3f3f));
	vector<vi>pos(n+1,vi(n+1));
	//d用于做floyd的最短路径
	rep(i,1,m){
		int u,v,w;
		cin>>u>>v>>w;
		g[u][v]=g[v][u]=min(g[u][v],w);
	}
	vector<vi>d=g;
	int res=0x3f3f3f3f;
	vi ans;
	auto dfs=[&](auto &&dfs,int i, int j)->void{
		if(!pos[i][j])	return;
		int k=pos[i][j];
		dfs(dfs,i,k);
		ans.pb(k);
		dfs(dfs,k,j);
	};
	auto get=[&](int i, int j,int k){
		ans.clear();
		ans.pb(k);
		ans.pb(i);
		dfs(dfs,i,j);
		ans.pb(j);
	};
	rep(k,1,n){
		//枚举i，j找最小环
		rep(i,1,k-1){
			rep(j,i+1,k-1){
				if(res>d[i][j]+g[i][k]+g[k][j]){
					res=d[i][j]+g[i][k]+g[k][j];
					get(i,j,k);
				}
			}			
		}
		
		//正常floyd
		rep(i,1,n){
			rep(j,1,n){
				if(d[i][j]>d[i][k]+d[k][j]){
					d[i][j]=d[i][k]+d[k][j];
					pos[i][j]=k;
				}
			}
		}
	}
	if(res==0x3f3f3f3f){
		cout<<"No solution."<<endl;
	}else{
		for(auto it:ans){
			cout<<it<<' ';
		}
		cout<<endl;
	}
}

signed main() {
	ios::sync_with_stdio(false);
	cin.tie(0);
	cout.tie(0);
//	freopen("1.in", "r", stdin);
	int _;
//	cin>>_;
//	while(_--)
	solve();
	return 0;
}

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1466334.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

1.系统调用接口

1.系统调用接口

1. 系统调用接口 1.1 Linux系统调用概念 系统调用&#xff08;systemcall&#xff09;&#xff1a; 所有的操作系统在内核里都有一些内建的函数&#xff0c;这些函数完成对硬件的访问和对文件的打开、读、写、关闭等操作。 Linux 系统中称这些函数为系统调用。这些函数实现了…
阅读更多...
Java学习笔记2024/2/23

Java学习笔记2024/2/23

今日内容 多态 包 final 权限修饰符 代码块 教学目标 能够说出使用多态的前提条件理解多态的向上转型理解多态的向下转型能够知道多态的使用场景包的作用public和private权限修饰符的作用描述final修饰的类的特点描述final修饰的方法的特点描述final修饰的变量的特点 第…
阅读更多...
Unity实现帧序列

Unity实现帧序列

一、目的 1.想实现序列帧效果 自己使用Animation一直无法实现动画播放效果 二、参考 1. Unity序列帧动画——Sprite图片集制作UI动画_unity 序列帧动画图集-CSDN博客 结果&#xff1a;很好用&#xff0c;能实现效果 三、实操 新建Image&#xff0c;增加Animator组件&#x…
阅读更多...
【行业交流】优积科技·国住人居与广东保利就学校、居住场景下模块化建筑技术的运用进行交流

【行业交流】优积科技·国住人居与广东保利就学校、居住场景下模块化建筑技术的运用进行交流

近日&#xff0c;保利发展控股集团股份有限公司&#xff08;以下简称“保利发展”&#xff09;、 优积建筑科技发展(上海)有限公司&#xff08;以下简称“优积科技”&#xff09;、国住人居工程顾问有限公司&#xff08;以下简称“国住人居公司”&#xff09;就模块化建造体系与…
阅读更多...
操作系统--多线程的互斥、同步

操作系统--多线程的互斥、同步

一、概念 在进程/线程并发执行的过程中&#xff0c;进程/线程之间存在协作的关系&#xff0c;例如有互斥、同步的关系。 1.互斥 由于多线程执行操作共享变量的这段代码可能会导致竞争状态&#xff0c;因此我们将此段代码称为临界区&#xff08;critical section&#xff09;…
阅读更多...
SIP 会话发起协议

SIP 会话发起协议

目录 会话发起协议 SIP SIP 系统的构件 SIP 的地址 SIP 特点 一个简单的 SIP 会话 会话描述协议 SDP 会话发起协议 SIP H.323 过于复杂&#xff0c;不便于发展基于 IP 的新业务。 会话发起协议 SIP (Session Initiation Protocol) 是一套较为简单且实用的标准&#xff0…
阅读更多...
CondaValueError: Malformed version string ‘~‘: invalid character(s)

CondaValueError: Malformed version string ‘~‘: invalid character(s)

使用conda 安装一些库时出现以下报错&#xff1a; CondaValueError: Malformed version string ~: invalid character(s)尝试进行更新conda conda upgrade -n base conda或者如果是环境方面的问题&#xff0c; conda upgrade -n base -c defaults --override-channels conda如…
阅读更多...
day41WEB 攻防-通用漏洞XMLXXE无回显DTD 实体伪协议代码审计

day41WEB 攻防-通用漏洞XMLXXE无回显DTD 实体伪协议代码审计

本章知识点&#xff1a; 1 、 XML&XXE- 原理 & 发现 & 利用 & 修复等 2 、 XML&XXE- 黑盒模式下的发现与利用 3 、 XML&XXE- 白盒模式下的审计与利用 4 、 XML&XXE- 无回显 & 伪协议 & 产生层面 配套资源&#xff08;百度网盘&#x…
阅读更多...
LLMs之Gemma：Gemma(Google开发的新一代领先的开源模型)的简介、安装、使用方法之详细攻略

LLMs之Gemma：Gemma(Google开发的新一代领先的开源模型)的简介、安装、使用方法之详细攻略

LLMs之Gemma&#xff1a;Gemma(Google开发的新一代领先的开源模型)的简介、安装、使用方法之详细攻略 导读&#xff1a;此文章介绍了Google推出的新一代开源模型Gemma&#xff0c;旨在帮助研发人员负责任地开发AI。 背景&#xff1a; >> Google长期致力于为开发者和研究人…
阅读更多...
基于R语言地理加权回归、主成份分析、判别分析等空间异质性数据分析

基于R语言地理加权回归、主成份分析、判别分析等空间异质性数据分析

在自然和社会科学领域有大量与地理或空间有关的数据&#xff0c;这一类数据一般具有严重的空间异质性&#xff0c;而通常的统计学方法并不能处理空间异质性&#xff0c;因而对此类型的数据无能为力。以地理加权回归为基础的一系列方法&#xff1a;经典地理加权回归&#xff0c;…
阅读更多...
spring cloud stream rabbit 4.0示例

spring cloud stream rabbit 4.0示例

参考链接 疑问 这里配置生产者、消费者 每一个都需要在yml配置&#xff0c;看起来很复杂&#xff0c;不知道有没有简单的配置方法 pom 添加依赖 方式一 <!--cloud rabbitMq 依赖--><dependency><groupId>org.springframework.cloud</groupId><ar…
阅读更多...
spring boot3登录开发-3(账密登录逻辑实现)

spring boot3登录开发-3(账密登录逻辑实现)

⛰️个人主页: 蒾酒 &#x1f525;系列专栏&#xff1a;《spring boot实战》 &#x1f30a;山高路远&#xff0c;行路漫漫&#xff0c;终有归途。 目录 前置条件 内容简介 用户登录逻辑实现 创建交互对象 1.创建用户登录DTO 2.创建用户登录VO 创建自定义登录业务异…
阅读更多...
H12-821_45

H12-821_45

45.如图所示,同一局域网中的四台路由器运行IS-IS,其中R1是DIS.则R2、R3、R4分别和R1建立邻接关系,R2、R3、R4之间不建立邻接关系。 A.正确 B.错误 答案&#xff1a;B 注释&#xff1a; 在广播链路上IS-IS路由器建立邻接关系和OSPF不同&#xff0c;所有IS-IS路由器之间都可以建…
阅读更多...
Github 2024-02-23 开源项目日报 Top10

Github 2024-02-23 开源项目日报 Top10

根据Github Trendings的统计&#xff0c;今日(2024-02-23统计)共有10个项目上榜。根据开发语言中项目的数量&#xff0c;汇总情况如下&#xff1a; 开发语言项目数量非开发语言项目4Python项目3TypeScript项目1HTML项目1Dart项目1Rust项目1 从零开始构建你喜爱的技术 创建周…
阅读更多...
关于el-select值的回显问题 : 框内显示label值还是value值

关于el-select值的回显问题 : 框内显示label值还是value值

<el-form-item label"状态" prop""><el-selectv-model"roleForm.state"class"m-2"size"large"style"width: 240px"placeholder"请选择状态"value-key"value"//value-key 与下面的ke…
阅读更多...
基于SVM的功率分类，基于支持向量机SVM的功率分类识别，Libsvm工具箱详解

基于SVM的功率分类，基于支持向量机SVM的功率分类识别，Libsvm工具箱详解

目录 支持向量机SVM的详细原理 SVM的定义 SVM理论 Libsvm工具箱详解 简介 参数说明 易错及常见问题 完整代码和数据下载链接：基于SVM的功率分类，基于支持向量机SVM的功率分类识别资源-CSDN文库 https://download.csdn.net/download/abc991835105/88862836 SVM应用实例， 基于…
阅读更多...
RK3568平台开发系列讲解（Linux系统篇）SPI 客户端通信

RK3568平台开发系列讲解（Linux系统篇）SPI 客户端通信

🚀返回专栏总目录 文章目录 一、spi_transfer二、spi_message三、初始化沉淀、分享、成长，让自己和他人都能有所收获！😄 SPI I/O模型由一组队列消息组成。我们提交一个或多个struct spi_message结构时，这些结构以同步或异步方式处理完成。单个消息由一个或多个struct sp…
阅读更多...
Swift Combine 使用调试器调试管道 从入门到精通二十六

Swift Combine 使用调试器调试管道 从入门到精通二十六

Combine 系列 Swift Combine 从入门到精通一Swift Combine 发布者订阅者操作者 从入门到精通二Swift Combine 管道 从入门到精通三Swift Combine 发布者publisher的生命周期 从入门到精通四Swift Combine 操作符operations和Subjects发布者的生命周期 从入门到精通五Swift Com…
阅读更多...
Linux的ACL权限以及特殊位和隐藏属性

Linux的ACL权限以及特殊位和隐藏属性

前言&#xff1a; ACL是什么&#xff1f; ACL&#xff08;Access Control List&#xff09;是一种权限控制机制&#xff0c;用于在Linux系统中对文件和目录进行细粒度的访问控制。传统的Linux权限控制机制基于所有者、所属组和其他用户的三个权限类别&#xff08;读、写、执行…
阅读更多...
今日arXiv最热NLP大模型论文：无需提示也能推理！Google DeepMind新研究揭示AI内在推理能力

今日arXiv最热NLP大模型论文：无需提示也能推理！Google DeepMind新研究揭示AI内在推理能力

在人工智能领域&#xff0c;大语言模型&#xff08;LLMs&#xff09;已经在各种复杂的推理基准测试中展现出了令人瞩目的性能。传统上&#xff0c;这些推理能力是通过精心设计的提示技术来激发的&#xff0c;例如少量示例提示&#xff08;few-shot prompting&#xff09;或零示…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023