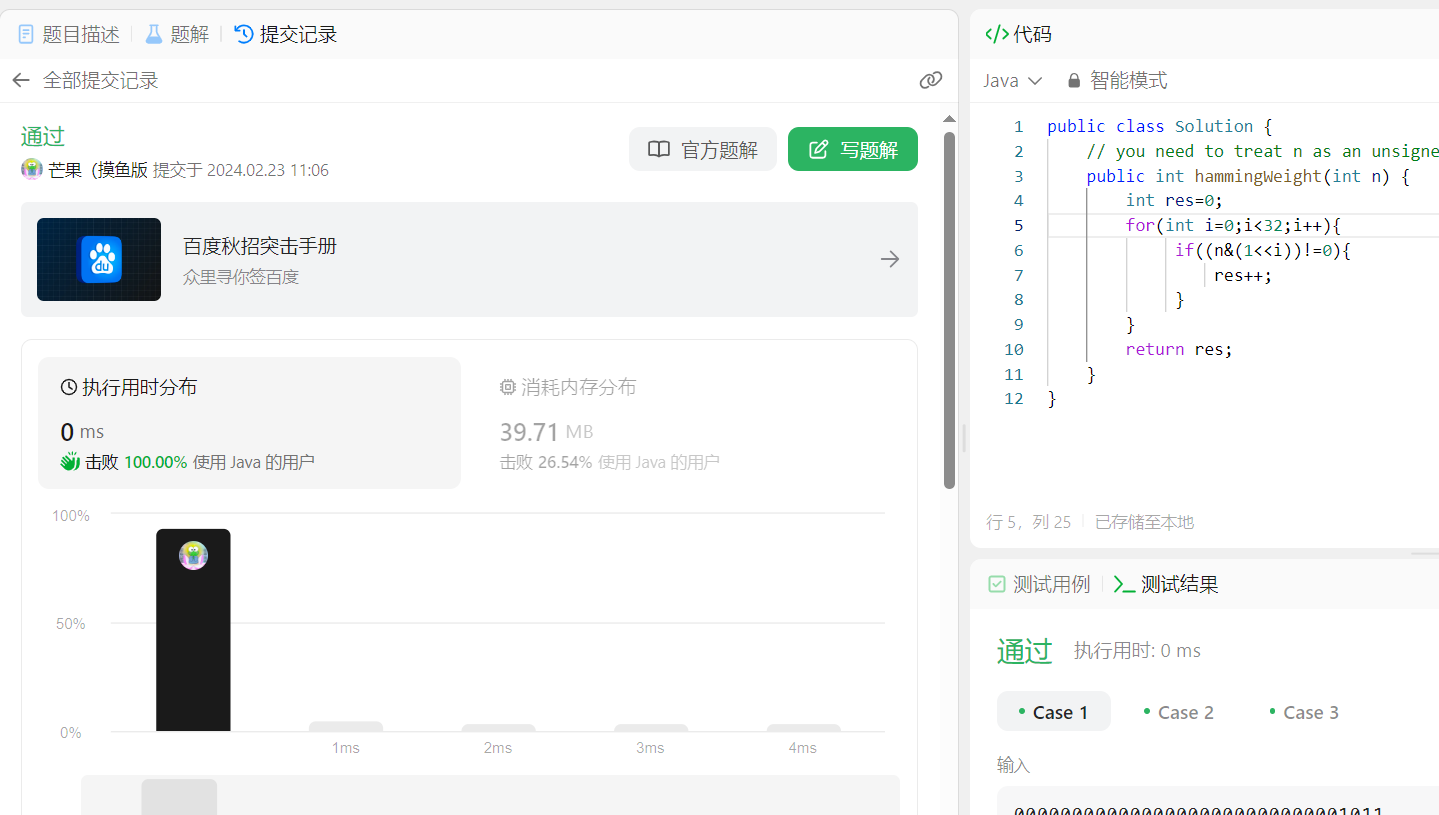
一、快速排序思路

快速排序特点：快

步骤：

1. 取一个元素p（第一个元素），使元素p归为；
2. 列表被p分成两部分，左边都比p小，右边都比p大；
3. 递归完成排序。

因此我们可以得到快速排序的大致框架：

def partition(data,left,right):
    pass

def quick_sort(data,left,right):
    if left < right:  #证明列表中最少有两个元素
        mid = partition(data,left,right)   # 进行归位
        quick_sort(data,left,mid-1)        #递归，对左边的元素进行快排
        quick_sort(data,mid+1,right)       #递归，对右边的元素进行快排

此时我们需要自己写出partition（归位函数），对元素进行归位。

二、归位函数

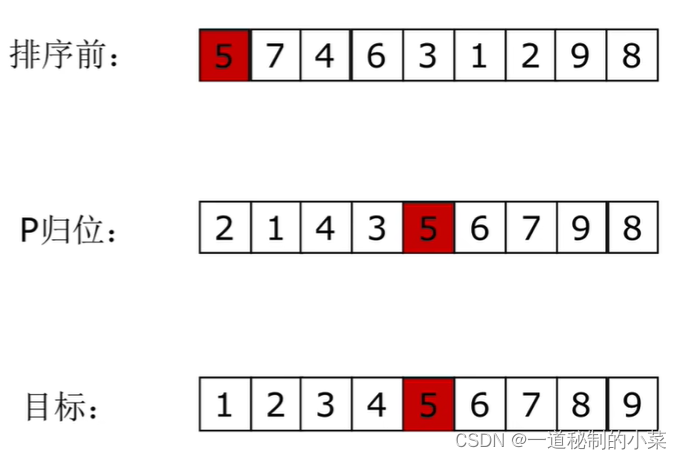
思路：例如下面这个数组：

具体思路流程：

1. 我们需要对5进行归位，需要将5取出来，此时左边5的位置有空位，（其中左右两个箭头分别对应left和right） 
2. 然后从右边的箭头开始，如果遇到比5小的数，将其放到5的位置（将2取出，放到5的位置）
3. 此时再从左边开始，如果遇到比5大的数，将其放到之前取数的位置（将7取出，放到2的位置）
4. 依次循环进行操作。直到left和right的箭头重合，此时将5放进去。

接下面我们尝试写出归位函数的代码：

def partition(data,left,right):
    tmp =li[left]   #先将第一个位置的元素取出，存起来
    while left < right:   #终止条件是当left = right时，循环结束，找到mid
        while left < right and li[right] >= tmp: # 从右边找如果比tmp大的数;且如果右边都是比tmp大的数，right会一直向左走，当left = right退出
            right -=1    #右边箭头向左进一步
        li[left] = li[right]  #此时将右边比tmp小的数放到左边
        print(li,"right")
        while left < right and li[left] <= tmp:   #左边的操作与右边的相同  
            left +=1    
        li[right] = li[left]   
        print(li,"left")
    li[left] = tmp   #把tmp归位
    
li = [5,7,4,6,3,1,2,9,8]
print(li)
partition(li,0,len(li)-1)
print(li)

输出结果如下：

最终我们得到归为函数。

三、快速排序

 最终，在得到归位函数之后，我们可以按照第一步的思路，写出快速排序的代码。

具体代码展示如下：

def partition(li, left, right):
    tmp = li[left]  # 先将第一个位置的元素取出，存起来
    while left < right:  # 终止条件是当left = right时，循环结束，找到mid
        while left < right and li[right] >= tmp:  # 从右边找如果比tmp大的数;且如果右边都是比tmp大的数，right会一直向左走，当left = right退出
            right -= 1  # 右边箭头向左进一步
        li[left] = li[right]  # 此时将右边比tmp小的数放到左边
        # print(li, "right")
        while left < right and li[left] <= tmp:  # 左边的操作与右边的相同
            left += 1
        li[right] = li[left]
        # print(li, "left")
    li[left] = tmp  # 把tmp归位
    return left


def quick_sort(data, left, right):
    if left < right:  # 证明列表中最少有两个元素
        mid = partition(data, left, right)
        quick_sort(data, left, mid - 1)
        quick_sort(data, mid + 1, right)


li = [5, 7, 4, 6, 3, 1, 2, 9, 8]
print(li)
quick_sort(li, 0, len(li) - 1)
print(li)

最终输出可得：

四、快速排序性质的分析

1. 时间复杂度

快速排序的效率（快速排序的时间复杂度）：O(nlogn)

(每一层的复杂度为n，一共有logn层)

2. 快速排序的问题

1. 最坏情况 （假如列表为[9,8,7,6,5,4,3,2,1],此时并不是每次分层logn，而是相当于至少一个数，时间复杂度相当于O()），解决思路，考虑倒序这种情况，选择第一个数改为随机选择一个数。
2. 递归（递归会消耗系统的资源）

即最好情况下时间复杂度接近于O(n)，最坏情况时间复杂度接近于O()。