本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：动态规划专栏
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

题目来源

本题来源为：

Leetcode1049. 最后一块石头的重量 II

题目描述

有一堆石头，用整数数组 stones 表示。其中 stones[i] 表示第 i 块石头的重量。

每一回合，从中选出任意两块石头，然后将它们一起粉碎。假设石头的重量分别为 x 和 y，且 x <= y。那么粉碎的可能结果如下：

如果 x == y，那么两块石头都会被完全粉碎；
如果 x != y，那么重量为 x 的石头将会完全粉碎，而重量为 y 的石头新重量为 y-x。
最后，最多只会剩下一块 石头。返回此石头 最小的可能重量 。如果没有石头剩下，就返回 0。

算法原理

本题的难点还是在于转化，将问题转化成目标和问题

1.状态表示

经验+题目要求

对于本题而言就是：

dp[i][j]表示：从前i个数中选，总和不超过j,此时的最大和

2.状态转移方程

问题已经转化成了01背包问题，分析跟01背包问题一样

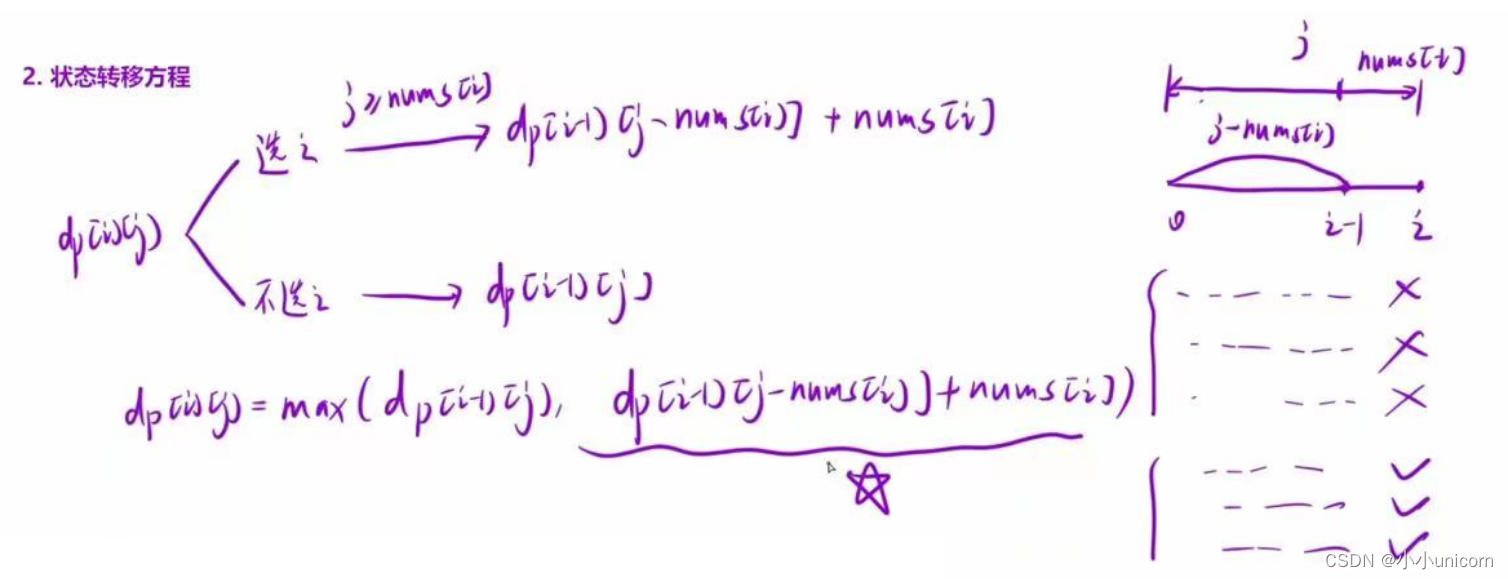
因此状态方程为：

 dp[i][j]=dp[i-1][j];
 if(j>=stones[i-1])
dp[i][j]=max(dp[i][j],dp[i-1][j-
stones[i1]]+stones[i-1]);

3.初始化

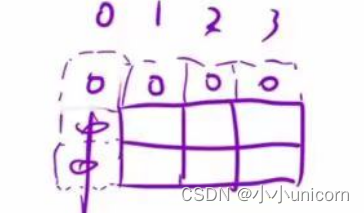
4.填表顺序

从上往下填买没一行

5.返回值

代码实现

动态规划的代码基本就是固定的四步：

1.创建dp表
2.初始化
3.填表
4.返回值

本题完整代码实现：

class Solution 
{
public:
    int lastStoneWeightII(vector<int>& stones) 
    {
        int sum=0;
        for(auto x:stones)
        sum+=x;
        int n=stones.size();
        int m=sum/2;

        //创建dp表
        vector<vector<int>> dp(n+1,vector<int>(m+1));

        //填表
        for(int i=1;i<=n;i++)
        {
            for(int j=1;j<=m;j++)
            {
                dp[i][j]=dp[i-1][j];
                if(j>=stones[i-1])
                    dp[i][j]=max(dp[i][j],dp[i-1][j-stones[i-1]]+stones[i-1]);
            }
        }
        //返回值
        return sum-2*dp[n][m];
    }
};

空间优化

代码实现：

class Solution 
{
public:
    int lastStoneWeightII(vector<int>& stones) 
    {
        int sum=0;
        for(auto x:stones)
        sum+=x;
        int n=stones.size();
        int m=sum/2;

        //创建dp表
        vector<int> dp(m+1);

        //填表
        for(int i=1;i<=n;i++)
        {
            for(int j=m;j>=stones[i-1];j--)
            {
                dp[j]=max(dp[j],dp[j-stones[i-1]]+stones[i-1]);
            }
        }
        //返回值
        return sum-2*dp[m];
    }
};