应用回归分析：泊松回归

news2025/2/24 10:23:32

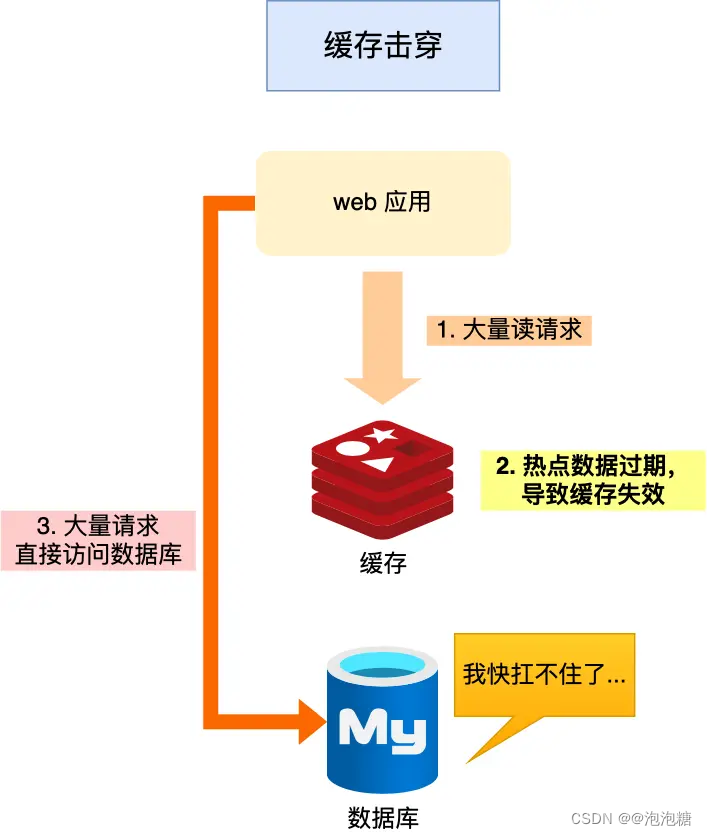
泊松回归是一种广泛用于计数数据的回归分析方法。它适用于响应变量是非负整数的情况，特别是当这些计数呈现出明显的离散分布时。泊松回归通过泊松分布的概率分布函数来建模计数数据，使其成为处理计数数据的自然选择。本文将介绍泊松回归的基本概念、应用场景、优缺点以及如何实施。

基本概念

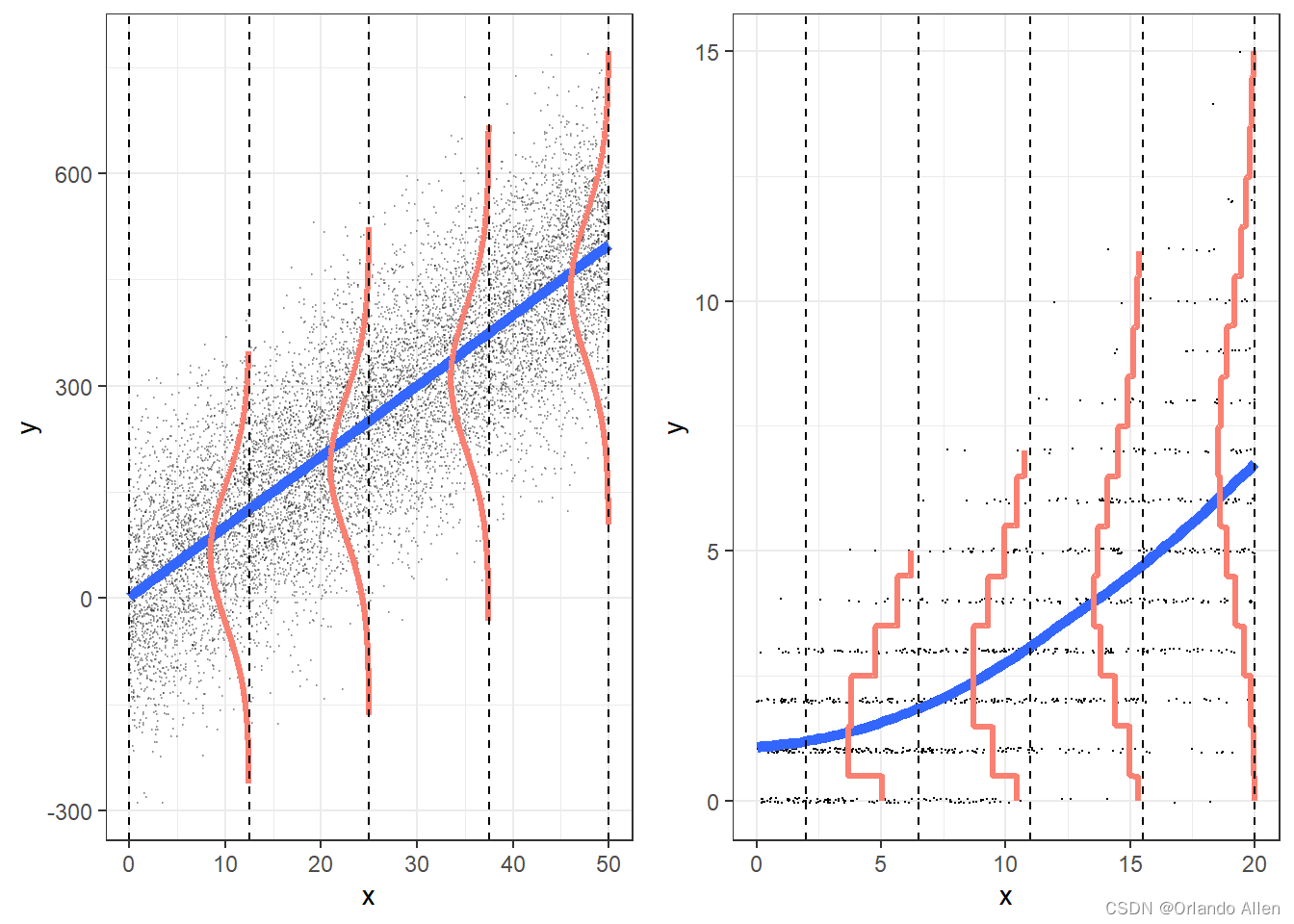
泊松回归基于泊松分布的假设，泊松分布是一种描述在固定时间或空间内发生某事件次数的概率分布。泊松回归模型的形式通常表示为：

应用场景

泊松回归适用于多种场景，尤其是那些涉及计数数据的场合，例如：

交通事故次数：预测某条道路或地区在一定时间内的交通事故次数。
疾病发病率：分析特定人群中疾病的发生次数。
网站访问量：预测网站在特定时间段内的点击次数或访问量。
零售销售：模拟商店在一定期间内的顾客数量或销售次数。

优缺点

优点：

专门化：泊松回归专门针对计数数据设计，能够有效处理非负整数响应变量。
灵活性：通过引入偏移量或使用泊松分布的变体（如负二项分布），可以处理过度离散的数据。

缺点：

过度离散：当数据显示出明显的过度离散（方差大于均值）时，泊松回归的假设可能不成立。
计数底限：泊松回归不适合处理有大量零计数的数据集，可能需要零膨胀模型来解决。

实施步骤

数据准备：确保响应变量为非负整数，且解释变量已适当选择和处理。
模型选择：根据数据的特性选择合适的泊松回归模型。如果数据显示过度离散，可以考虑使用负二项回归。
模型训练：使用统计软件包（如R的glm函数或Python的statsmodels库）来训练泊松回归模型。
模型评估：通过检验统计量（如伪R^2）和残差分析来评估模型的拟合度和预测能力。
模型应用：使用模型进行预测和解释。

示例代码

import pandas as pd
import statsmodels.api as sm

# 示例数据，假设DataFrame名称为df
# df = pd.DataFrame({
#     'X1': [...],  # 解释变量1
#     'X2': [...],  # 解释变量2
#     'Counts': [...]  # 计数数据，即响应变量
# })

data = {
    'X1': [1, 2, 3, 4, 5],
    'X2': [2, 2, 3, 4, 5],
    'Counts': [0, 1, 2, 3, 4]
}
df = pd.DataFrame(data)

# 定义解释变量和响应变量
X = df[['X1', 'X2']]  # 解释变量
y = df['Counts']  # 响应变量

X = sm.add_constant(X)

# 拟合泊松回归模型
poisson_model = sm.GLM(y, X, family=sm.families.Poisson()).fit()

# 查看模型摘要
print(poisson_model.summary())

# 进行预测（例如，使用与训练数据相同的数据进行预测）
predictions = poisson_model.predict(X)

print(predictions)

在这个例子中，我们首先创建了一个包含解释变量和响应变量的DataFrame。然后，我们使用statsmodels的泛化线性模型（GLM）类和泊松分布族来拟合模型。最后，我们查看了模型的统计摘要，并使用模型对一些数据进行了预测。