【深蓝学院】移动机器人运动规划--第6章模型预测控制(MPC)与运动规划--笔记

0. Outline

在这里插入图片描述

1. Reactive Control（反应式控制）

控制学中的 “Reactive Control” 通常指的是一种控制策略，它依赖于系统对特定事件或变化的即时反应，而不是按照预定的计划或策略行动。这种控制往往是基于当前的传感器输入来做出决策，而不是提前编程的指令。

与 “Reactive Control” 相对的是 “Proactive Control” 或者 “Feedforward Control”，后者是基于对系统将要发生的变化的预测和规划的控制方法。

如果我们提到 “Feedback Control”（反馈控制），则指的是系统输出会被反馈并与期望的参考值相比较，然后根据这种比较的结果来调整输入，以减少输出和参考值之间的误差。反馈控制是一种常见的控制机制，可以是连续的也可以是离散的，用于保证系统的稳定性和性能。

因此，尽管 “Reactive Control” 可以涵盖反馈机制作为对即时变化的响应，但它并不完全等同于 “Feedback Control”。反馈控制更侧重于基于输出和目标之间的比较来调整输入的过程。

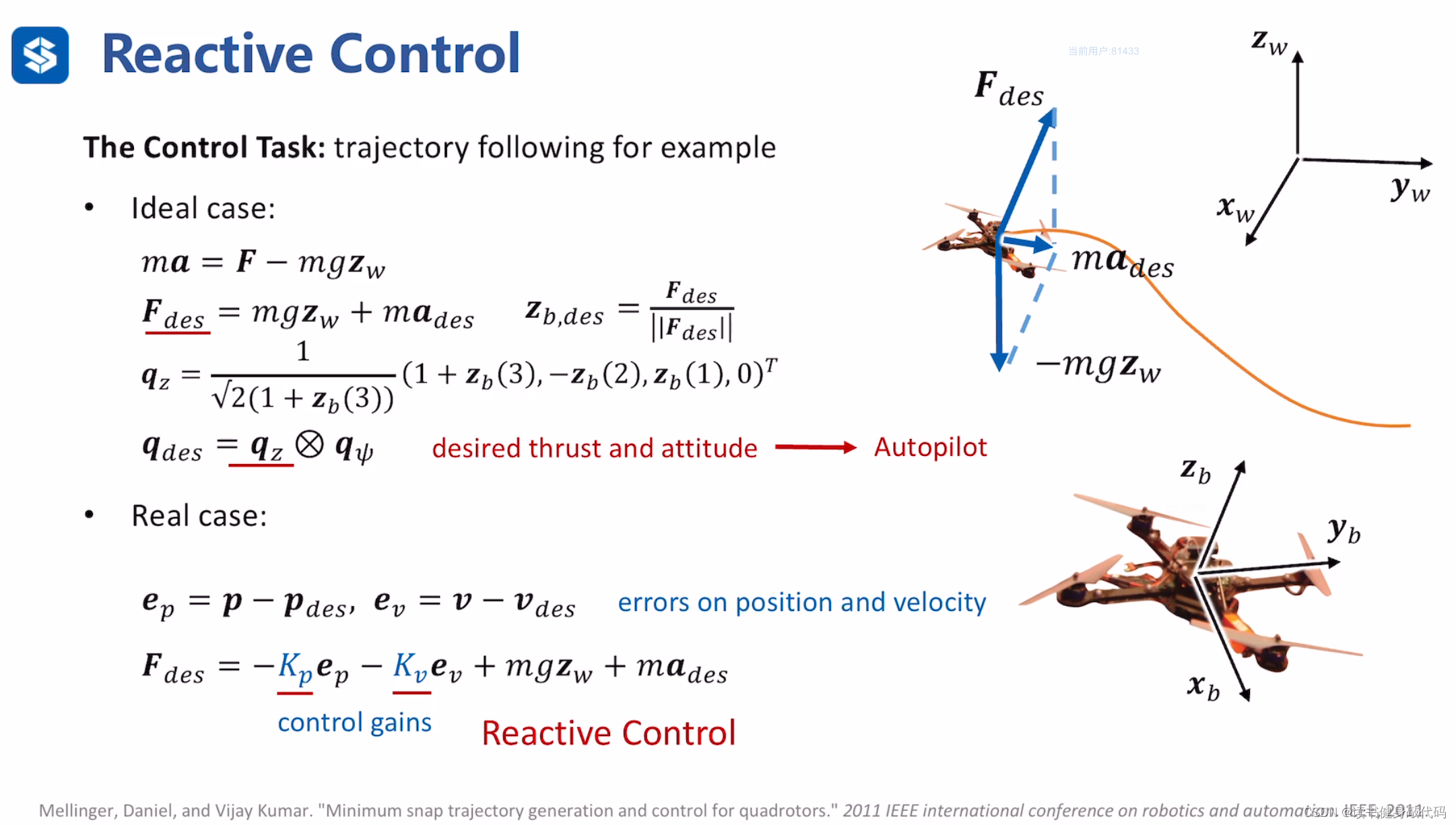
在这里插入图片描述
ref[1]，理想情况下，Multicopters的控制是由生成的traj
traj的生成，如果基于flat output，得到flat otput $z^*(t)$ 后，通过flatness transformation得到 $x^*(t)=\{p,v,R,\omega\},u^*(t)=\{f(推力),\tau(扭矩)\}$ ，

理想情况下，Multicopters会沿着规划出的轨迹进行飞行，根据z轴desire和world z解算出tilt，而tilt和yaw可以计算出R，可算出具体推力，再使用动力学方程 $p=p_0+v_0t+\frac{1}{2}at^2$ 等计算出Multicopters pose。

但实际情况是会受到风阻，油门曲线误差等因素的影响，实际运动时实际 $p ， v$ 与理想 $p ， v$ 会存在误差，Reactive Control在计算预期推力 $F_{des}$ 会考虑 $p, v$ 误差，引入比例因子(类似于PID中的P)。

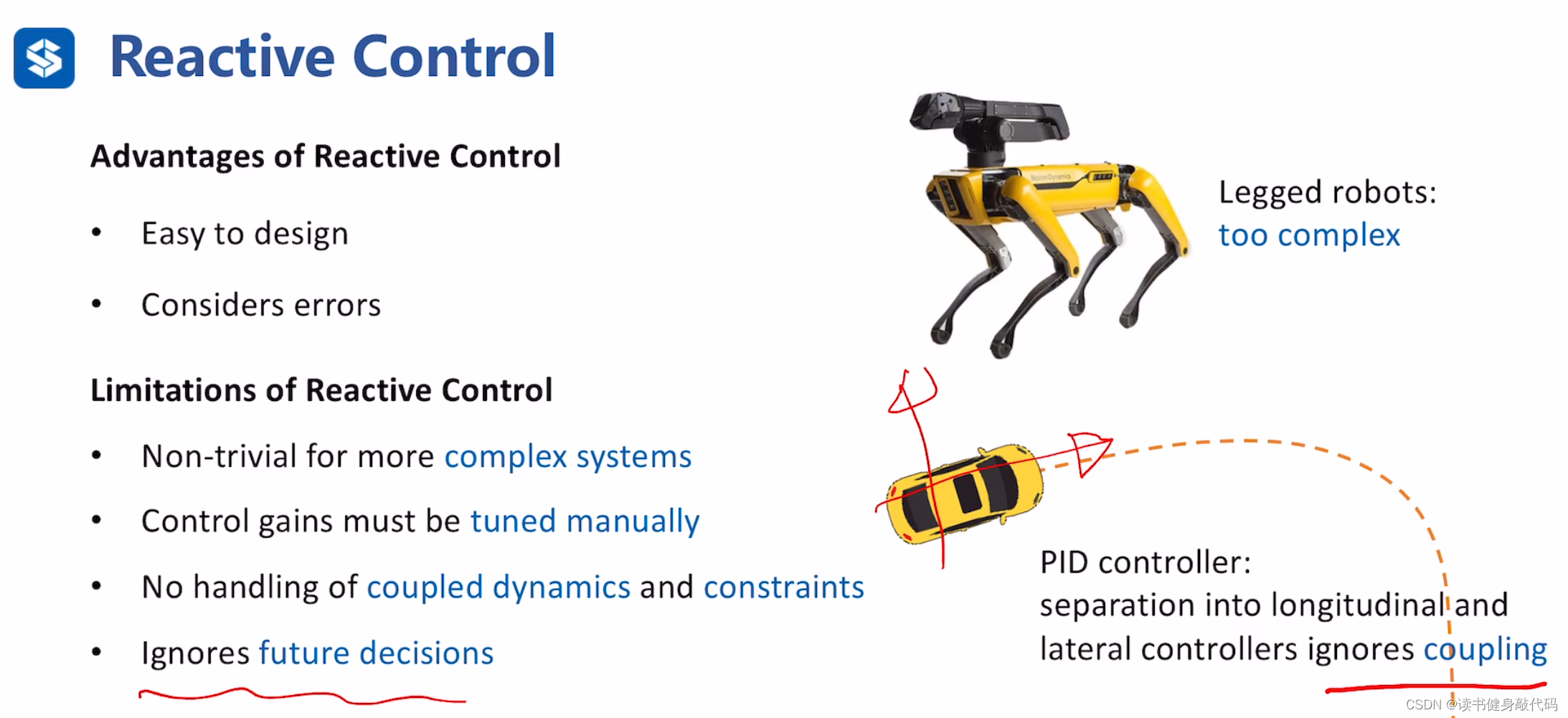
在这里插入图片描述
pros & cons

pros：易实现，考虑了实际误差。

cons：

复杂的系统求解需要考虑更多，Reactive Control可能不够。
调参麻烦
无法解决具有耦合关系的动态性和约束。
无法使用未来时刻的信息做出决策（如看到红灯提前减速）

2. Optimal Control（最优控制）

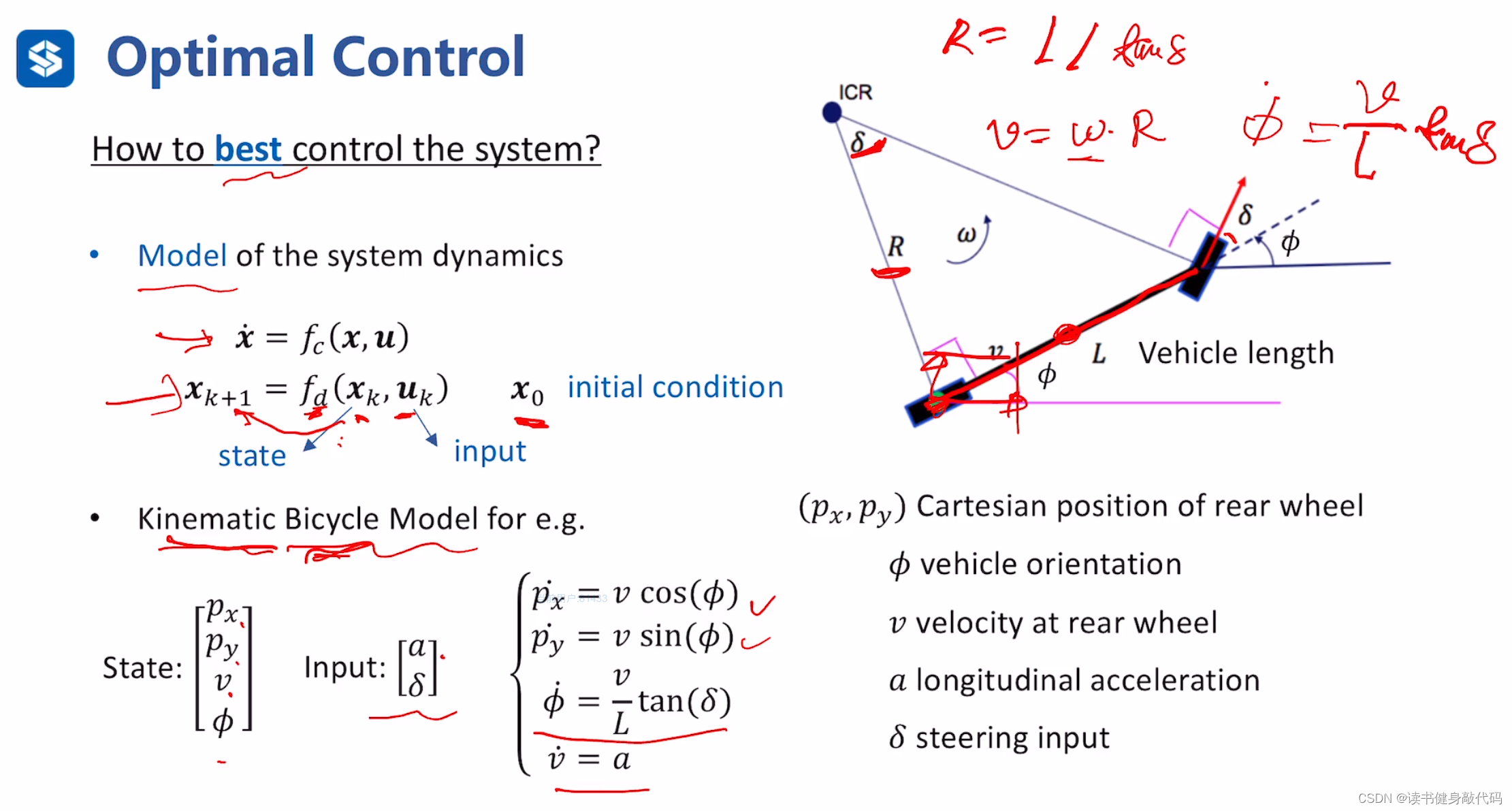
在这里插入图片描述
根据几何约束和动力学构建出自行车的动力学模型，汽车和自行车的模型具有相似性，只是自行车为2个轮子，汽车4个。

由初始时刻状态和输入量即可算出末端状态。

还有其他类型的自行车模型，此处仅介绍最简单的一种建模形式。

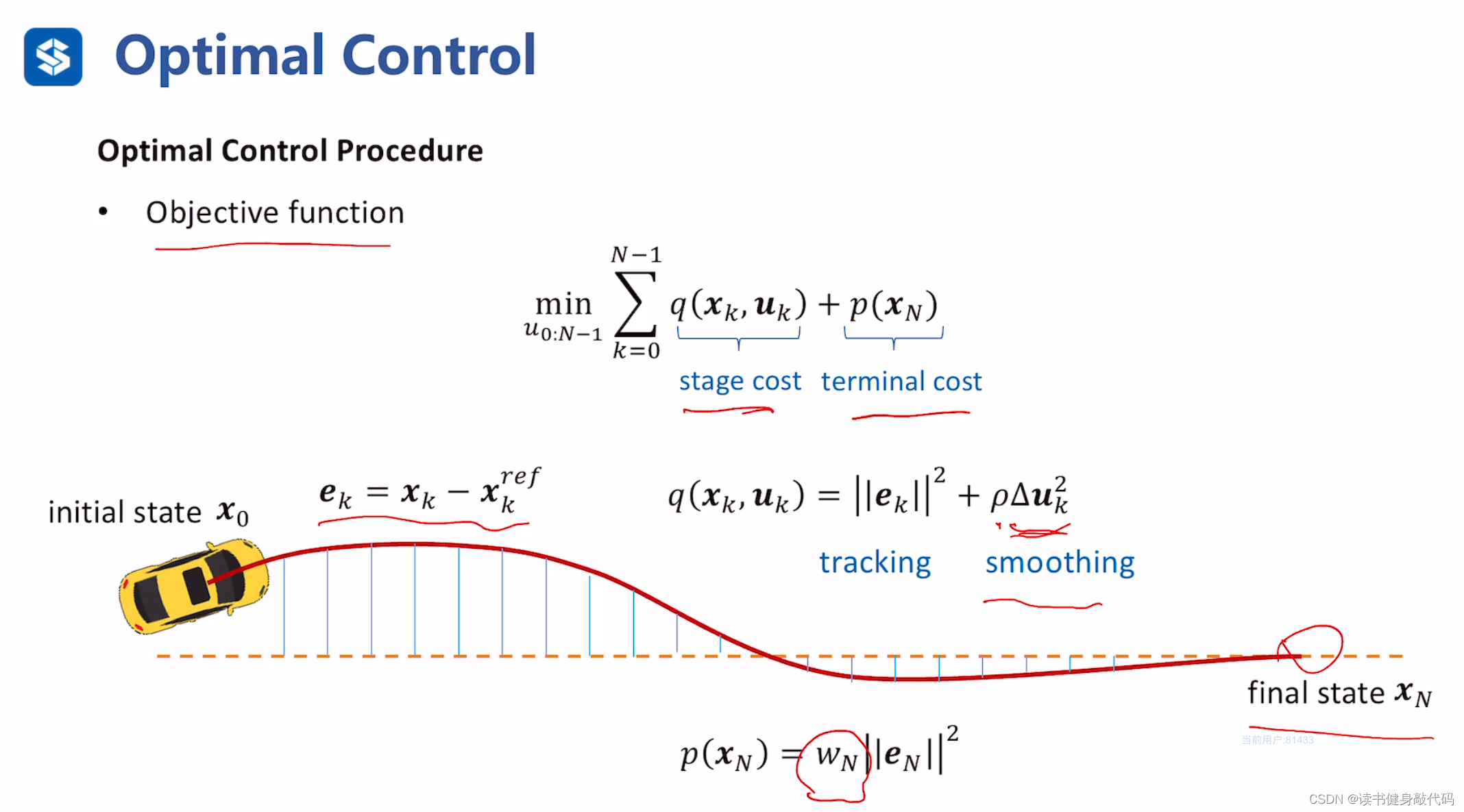
在这里插入图片描述
以跟随车道线为目标，建立目标函数：
分为两部分：stage cost + terminal cost
两部分形式可以相同也可以不同
stage cost中 $e_k$ 是偏离车道线的误差，加上平滑项，不希望频繁打杆，使控制更加顺滑。
terminal cost这里与stage cost形式类似，权重不同，如果增大terminal cost权重，就更希望车最终到达设定的末状态。

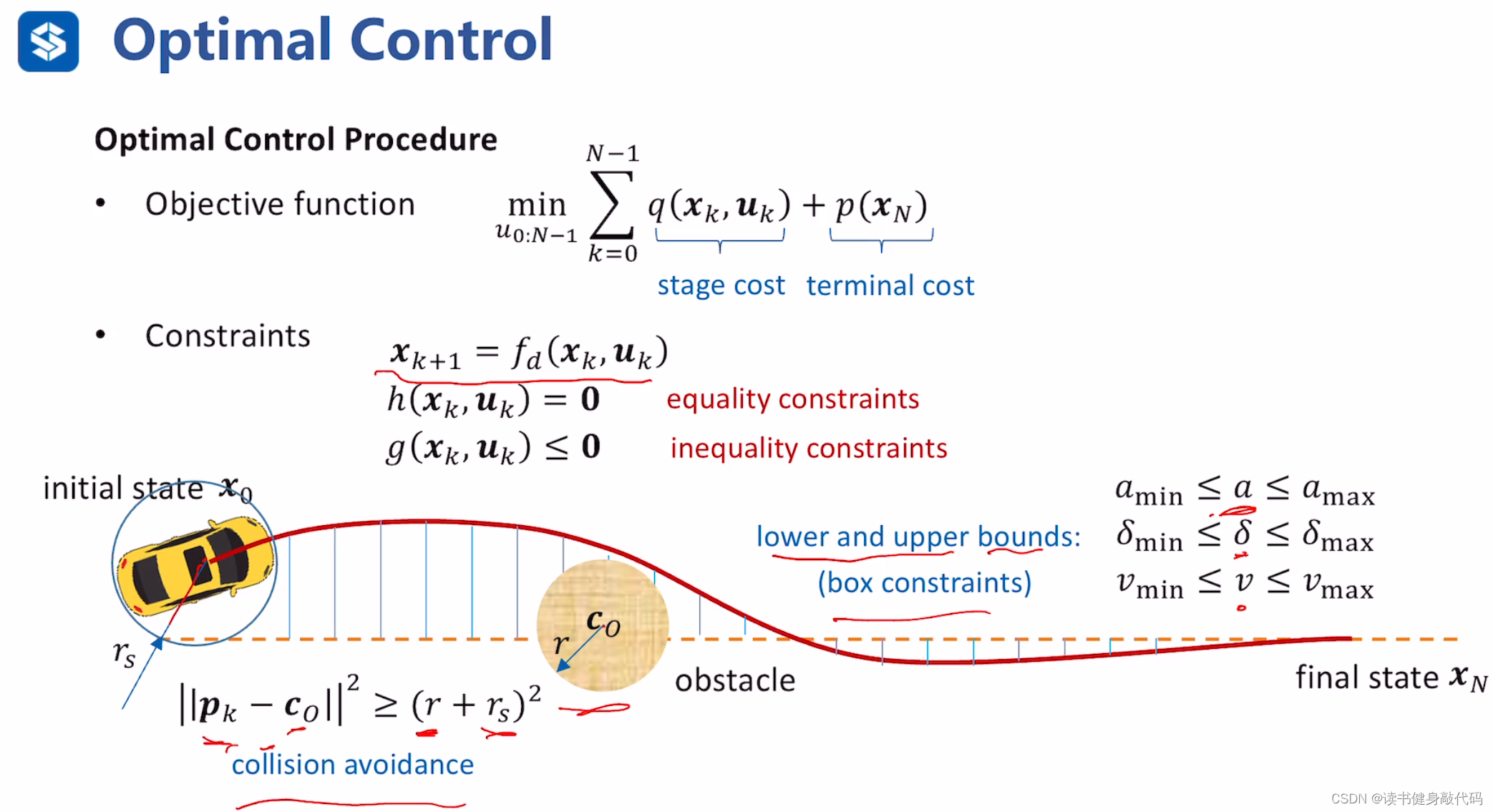
在这里插入图片描述
考虑等式约束（边界条件等）和不等式约束（控制限制等），避障（矩障碍物圆心距离大于障碍物半径）

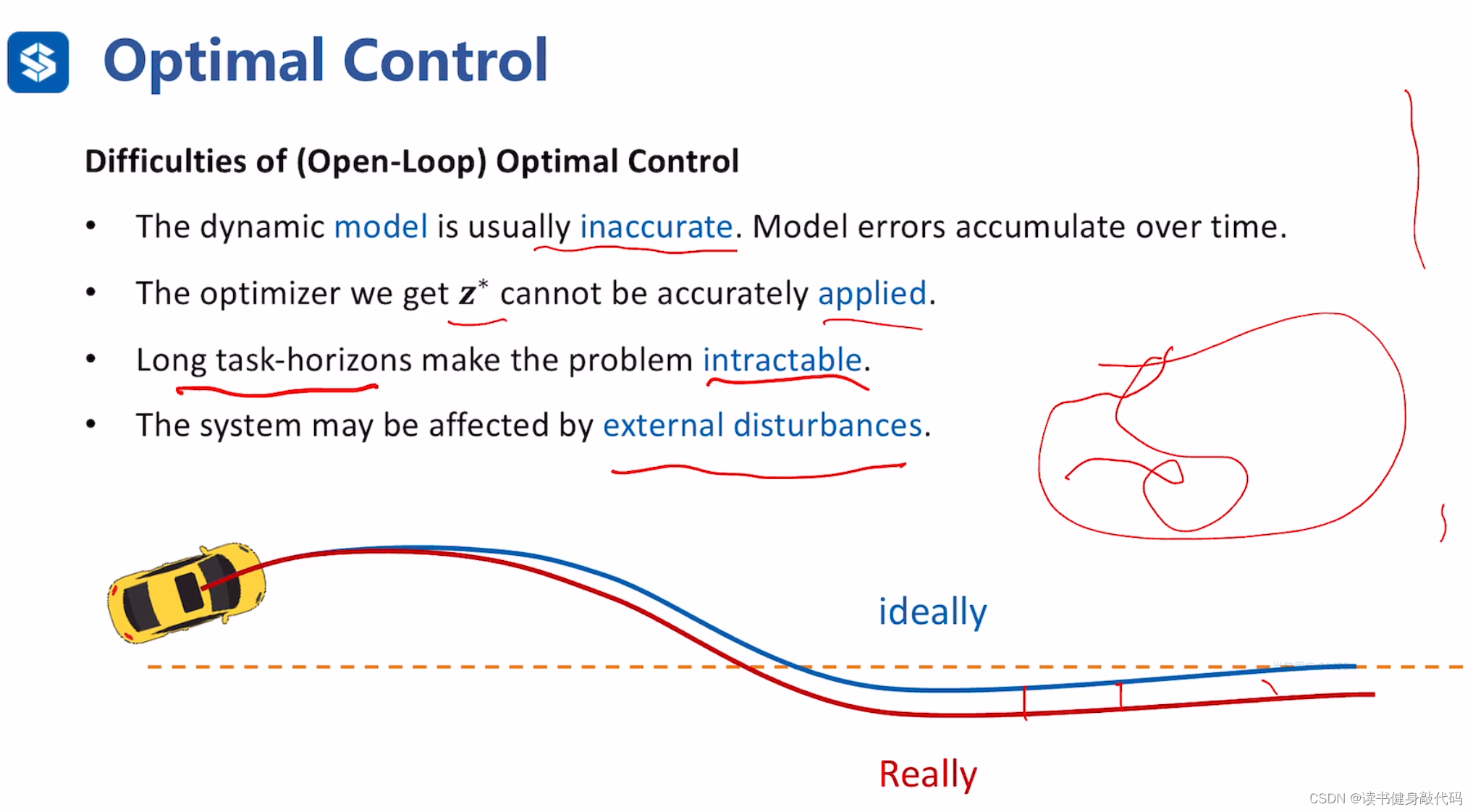
在这里插入图片描述
最优控制流程。

在这里插入图片描述
开环最优控制存在的问题：

模型不准确，不适配，误差会累积。
$z^*(t)$ 无法准确被执行，即执行误差。
长时间控制问题使问题不可解。
外部扰动会对系统控制产生影响。

简单理解：reactive control能使用误差信息，但无法处理具有耦合关系的约束等，optimal control处理了约束问题，但无法解决长时间控制问题，且没考虑扰动问题。

MPC结合了reactive control和optimal control的优点。

3. Model Predictive Control (MPC)

3.1 Preliminaries

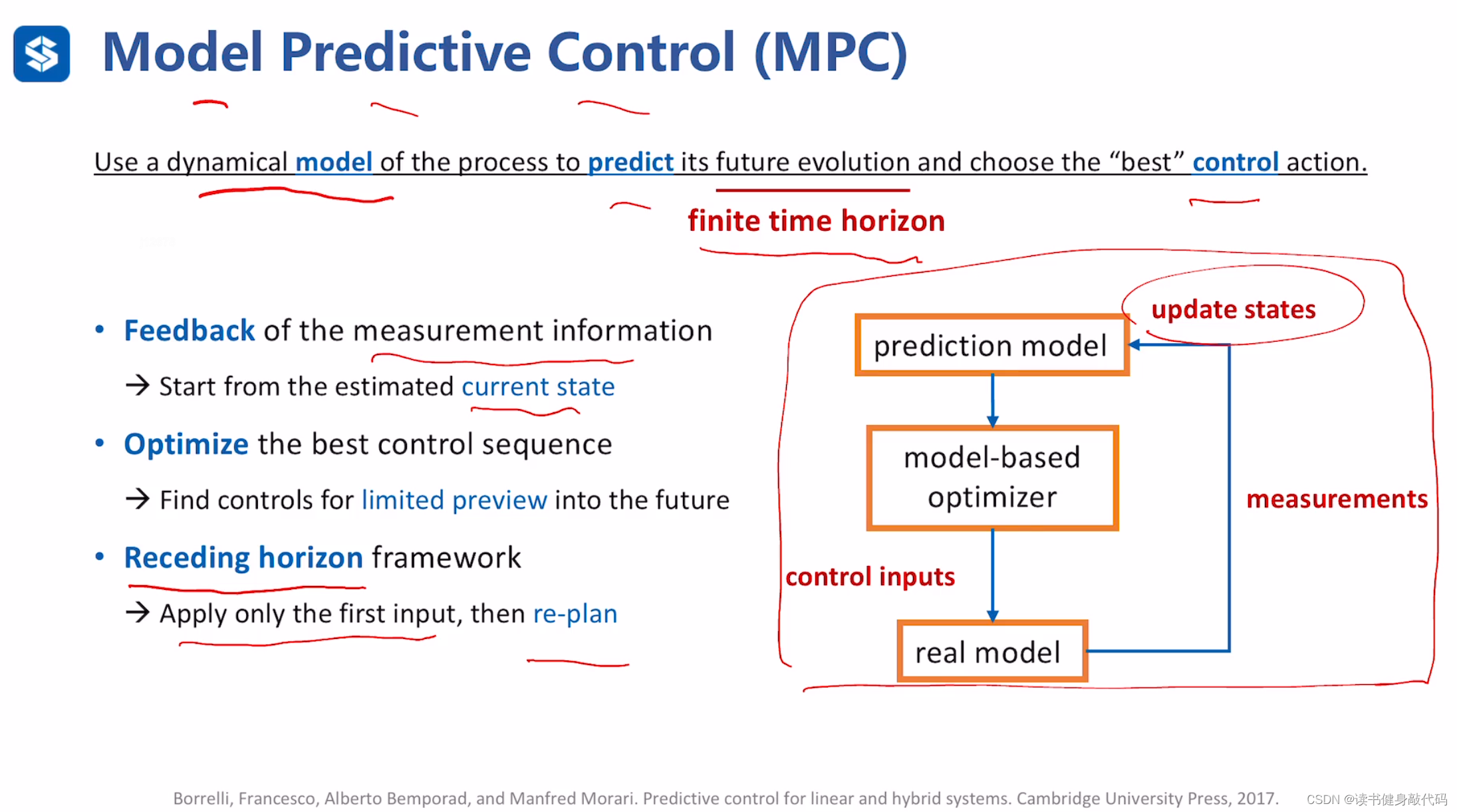
在这里插入图片描述
ref[2]。

MPC只预测一小段的轨迹，然后只执行一部分，然后根据measurements继续执行预测，控制，测量的循环。

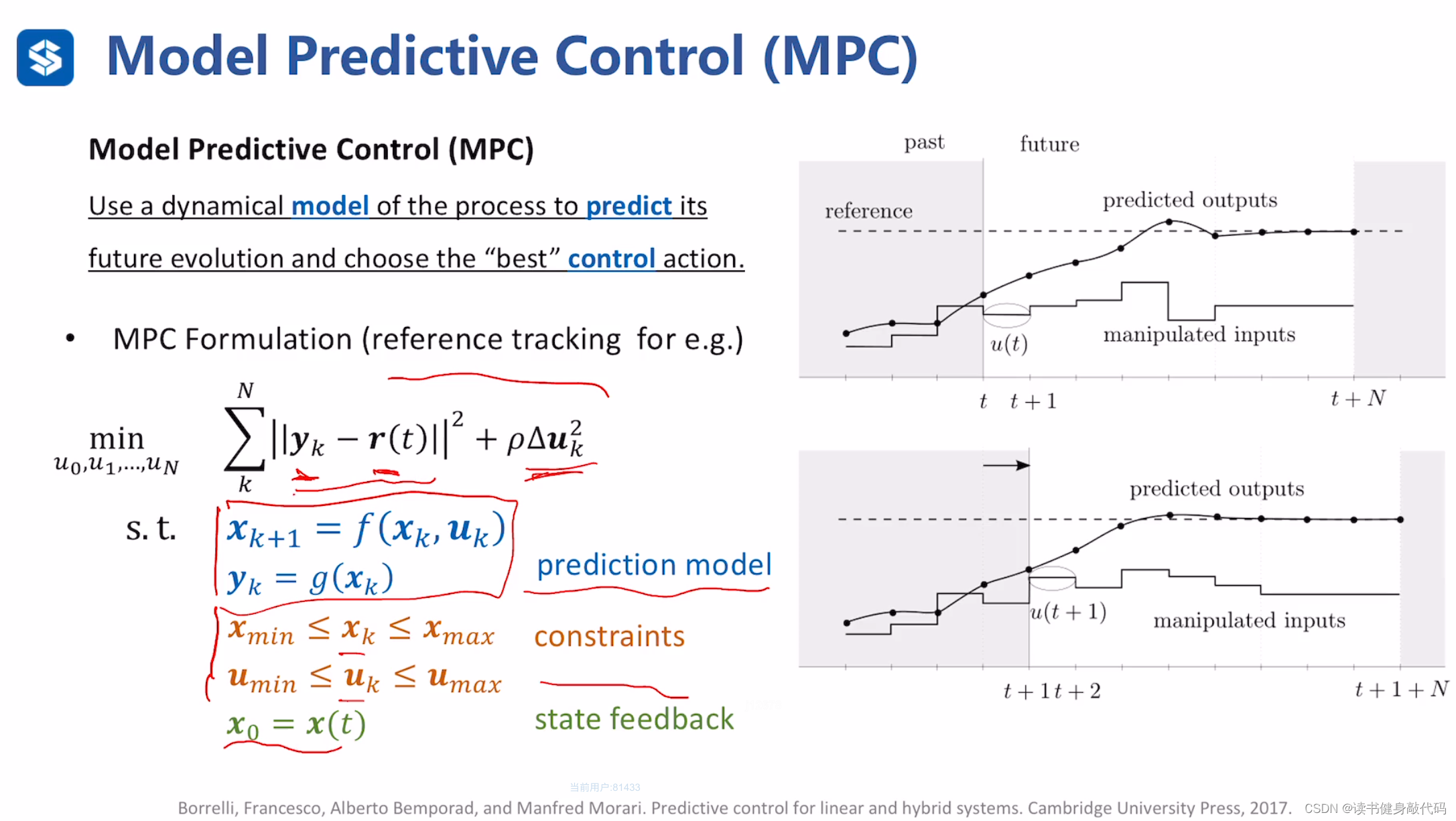
在这里插入图片描述
MPC Formulation，cost function和最优控制类似。

在这里插入图片描述

别名：
Open Loop Optimal Feedback 开环最优反馈
Reactive Scheduling 响应式调度
Receding Horizon Control 滚动时域控制，滚动优化控制。

考虑未来的信息（相对optimal control而言）
补偿误差，
减小问题的规模（每次只求解一小段问题，warm-start 即t和t+1时刻MPC求解只相差了一个time step，t时刻解可作为t+1时刻求解的初值，加快收敛）。

在这里插入图片描述
MPC源自业界，后来才在学界有了理论研究，学习MPC要持有学以致用的心态。

在这里插入图片描述
两个MPC的应用：
ref[3] 四旋翼坏掉一个桨的MPC控制悬停及降落。
ref[4] 轮腿式机器人的步态生成。

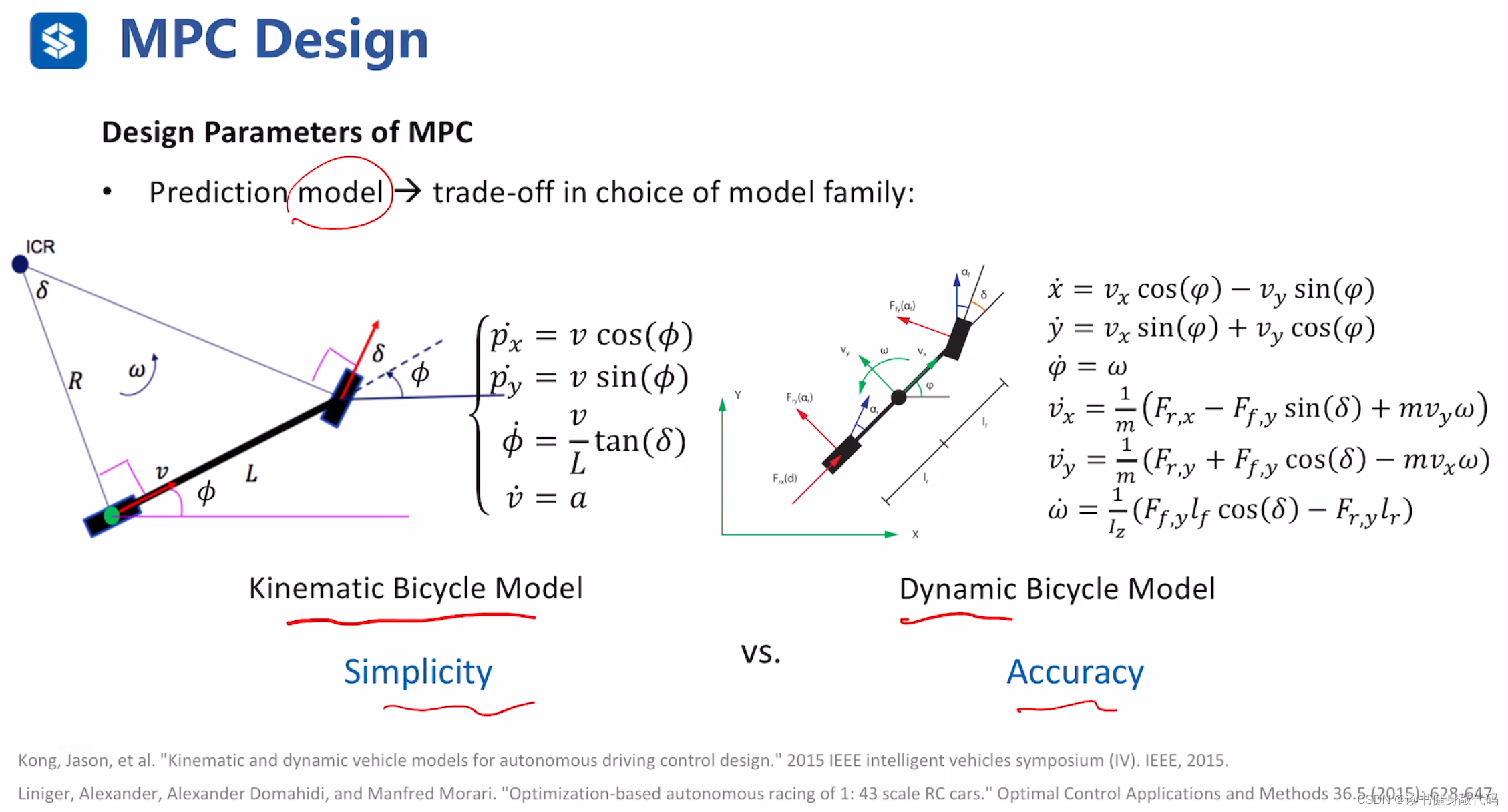
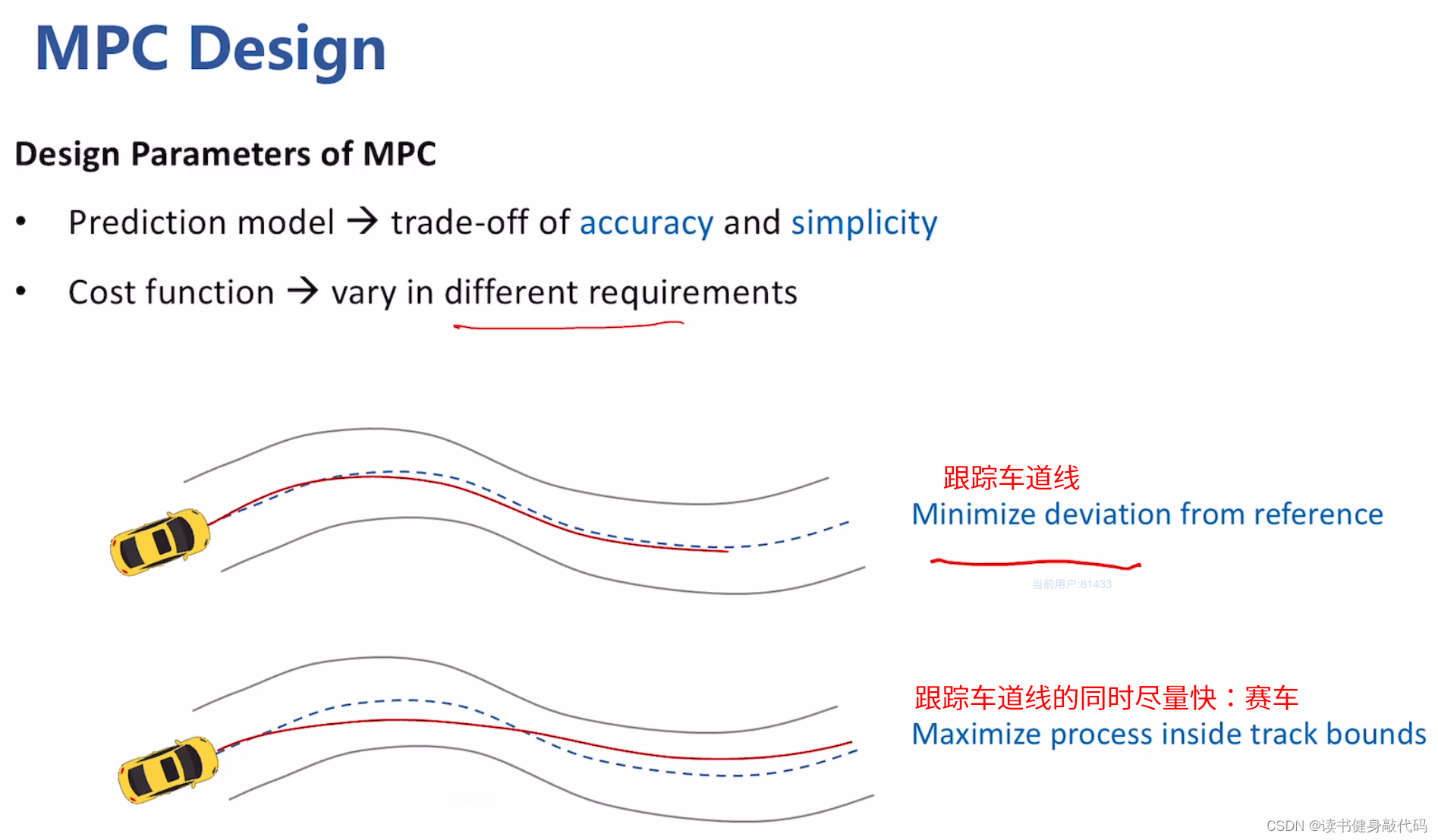
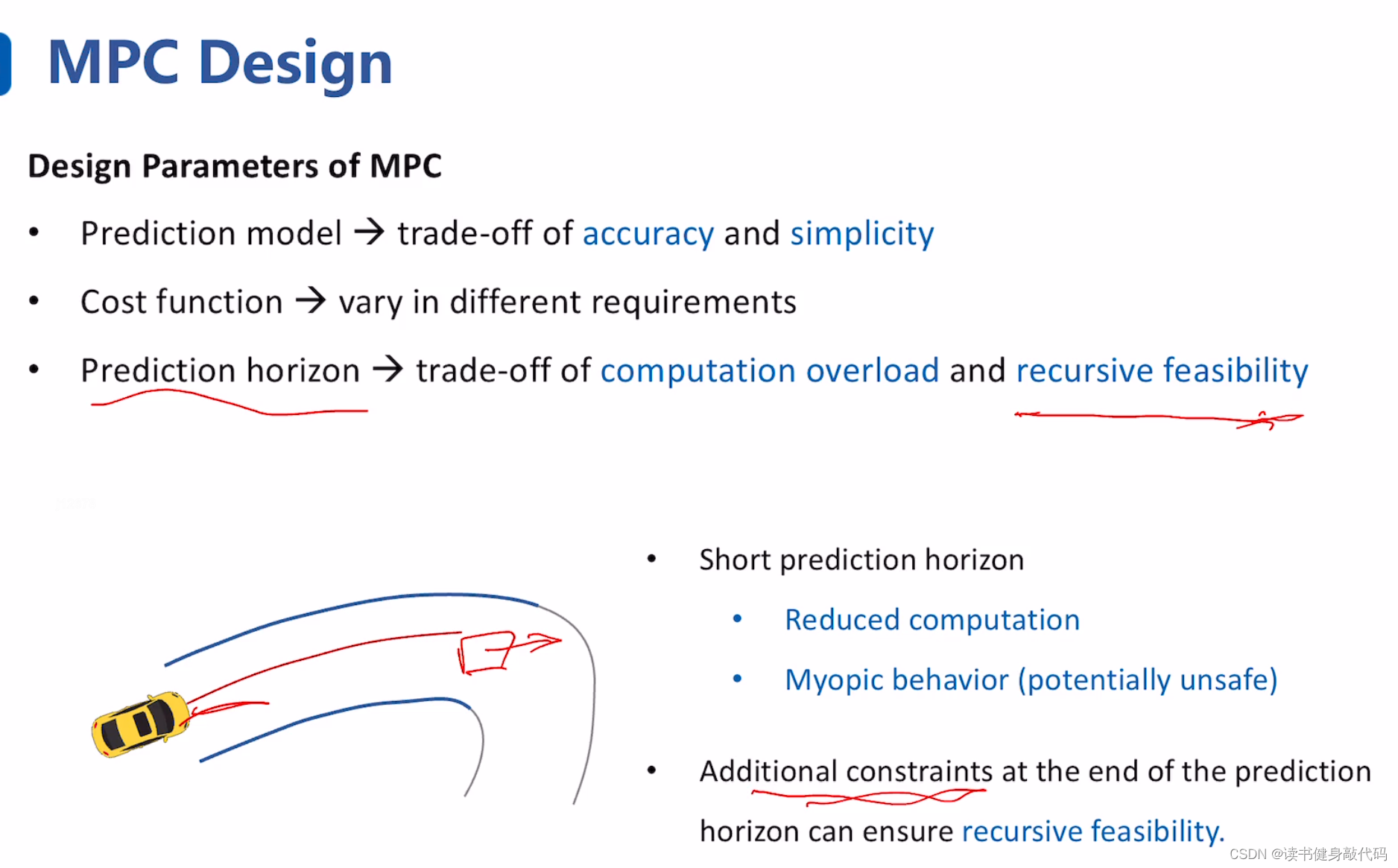
在这里插入图片描述

MPC的设计：

预测模型的选择：是求解精读和复杂性的trade-off，ref [5,6]（大部分自动驾驶，工业AGV使用左边模型就足够)。
MPC cost funtion设计：不同要求会有不同的参数设计
预测时长PH：最优控制的预测时长是整段轨迹时长，而MPC只针对一小段轨迹。recursive feasiability：虽然只优化一小段，但是保证问题一定有解，常见实现方法是给PH终点的末状态增加约束。(在ref[8]中有所提及)

3.2 Linear MPC

3.2.1 Unconstrained Case

先讲解简单的无约束MPC：
在这里插入图片描述
线性MPC假设系统模型是线性的，即系统的未来状态可以用当前状态和控制输入的线性函数来表示。由于线性模型的预测较为简单且计算量较小，线性MPC在工业和工程应用中非常流行。

$x_k$ 是系统状态， $y_k$ 是系统输出，一般是系统状态的一部分或者线性组合。

在这里插入图片描述
线性系统cost funtion为二次costs，系数矩阵 $P, Q, R$ 均为正定，保证问题有解。

costs可能也是stage cost + terminal cost

在这里插入图片描述

把目标函数中系统未来N个时刻的状态组成的向量 $z$ 表示成关于未来的控制输入和初始状态 $x_0$ 的形式，带入原cost function可进一步整理。

在这里插入图片描述
ref[7]

对整理过后的cost funtion进行优化，简单的思路是求导等于0，解出最优解 $z^*=-H^{-1}F^Tx_0$ ，发现线性系统最优解竟然与初始状态 $x_0$ 呈线性关系，所以无约束的线性MPC又称为线性状态反馈，最优解又称为batch solution。

这种linear MPC的推导（把系统状态 $x$ 和输入 $u$ 分开写）又叫做condense MPC，如果把 $x, u$ 放在一起表示，则可以推导出非稠密的MPC(Non-condensed MPC)，ref[7]：
在这里插入图片描述

推导出来的系数矩阵是稀疏的，不过non-condenced MPC会引入额外的系统状态转移约束，在无约束linear MPC中一般不使用，在有约束的情况下可能比dense MPC求解更快。

在这里插入图片描述

condensed-MPC的batch solution存在解析解，但需要对大矩阵 $H$ 求逆，时间复杂度 $O(n^3)$ ，需要考虑更快的求解方法，引出了接下来要讲的LQR方法。

3.2.2 LQR线性二次调节器（控制器）

在这里插入图片描述
使用了问题的序列化结构。

首先介绍贝尔曼法则Bellman princlple：
如果一个问题可分为很多步来实现，该问题的最优解中，那么整个问题在某个状态之后的最优解部分，仍然是剩余的子问题的最优解。

如MPC中整个问题最优解 $z^*$ 为 $x^*=(x_0^*,x_1^*,\cdots x_k^*,\cdots,x_N^*)$ $u^*=(u_0^*,u_1^*,\cdots,u_k^*,\cdots,u_{N-1}^*)$
那么在 $x_k$ 时，有子问题“从 $x_k$ 到 $x_N$ 的最优解”，该子问题的最优解与 $z^*$ 中对应的部分相同，即 $x^*=(x_k^*,\cdots,x_N^*)$ $u^*=(u_k^*,\cdots,u_{N-1}^*)$

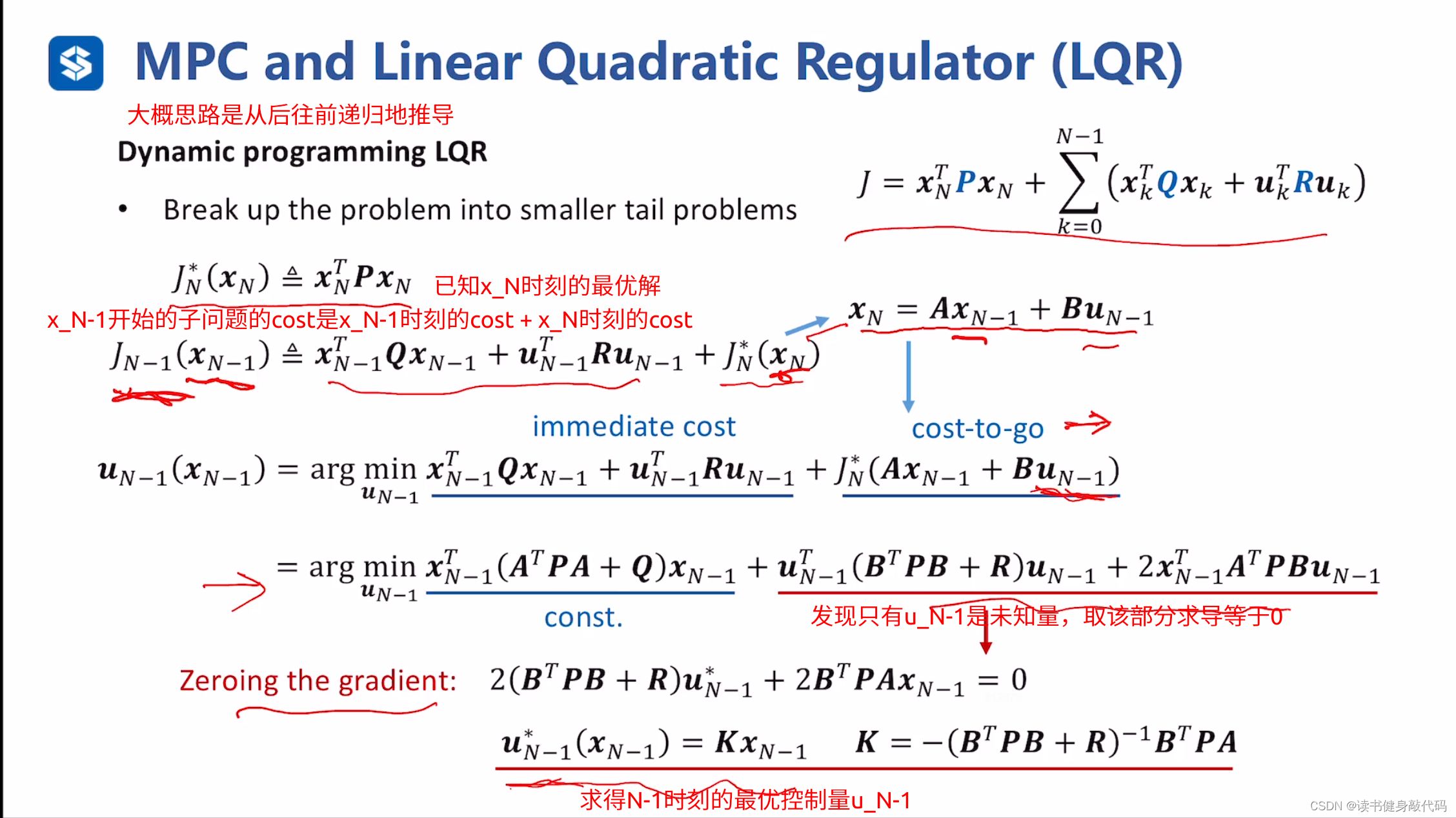
在这里插入图片描述
求出的 $u_{N-1}$ 仍然只和 $x_{N-1}$ 有关。

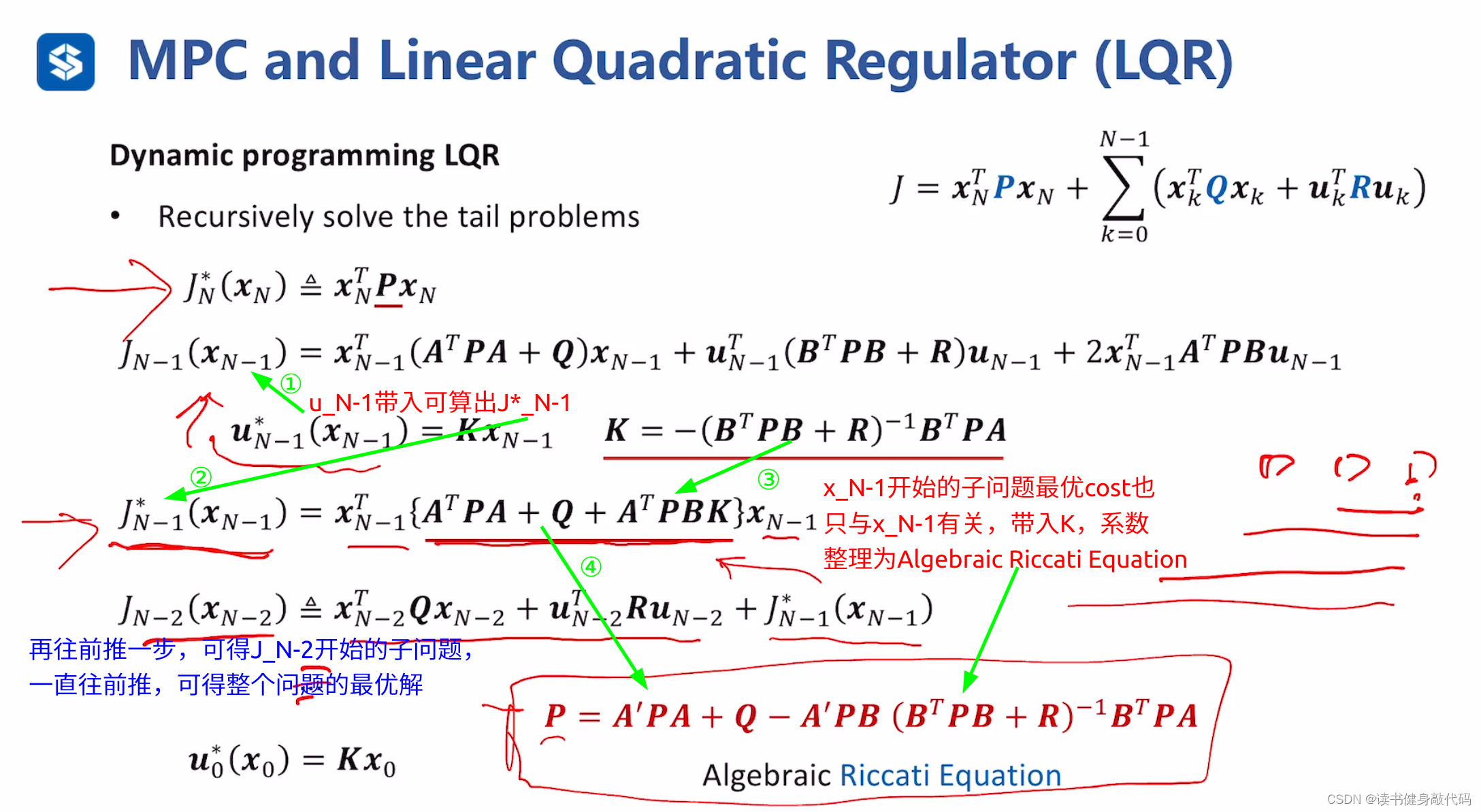
在这里插入图片描述
最终可推导出代数Riccati方程。

LQR小结：

LQR比batch solution计算效率高，为线性复杂度。
MPC可以施加约束，而LQR无法施加。
MPC通常用于有限的PH，而LQR的PH趋于无穷。
MPC更通用，LQR只能用于目标函数为二次型的cost funtion。

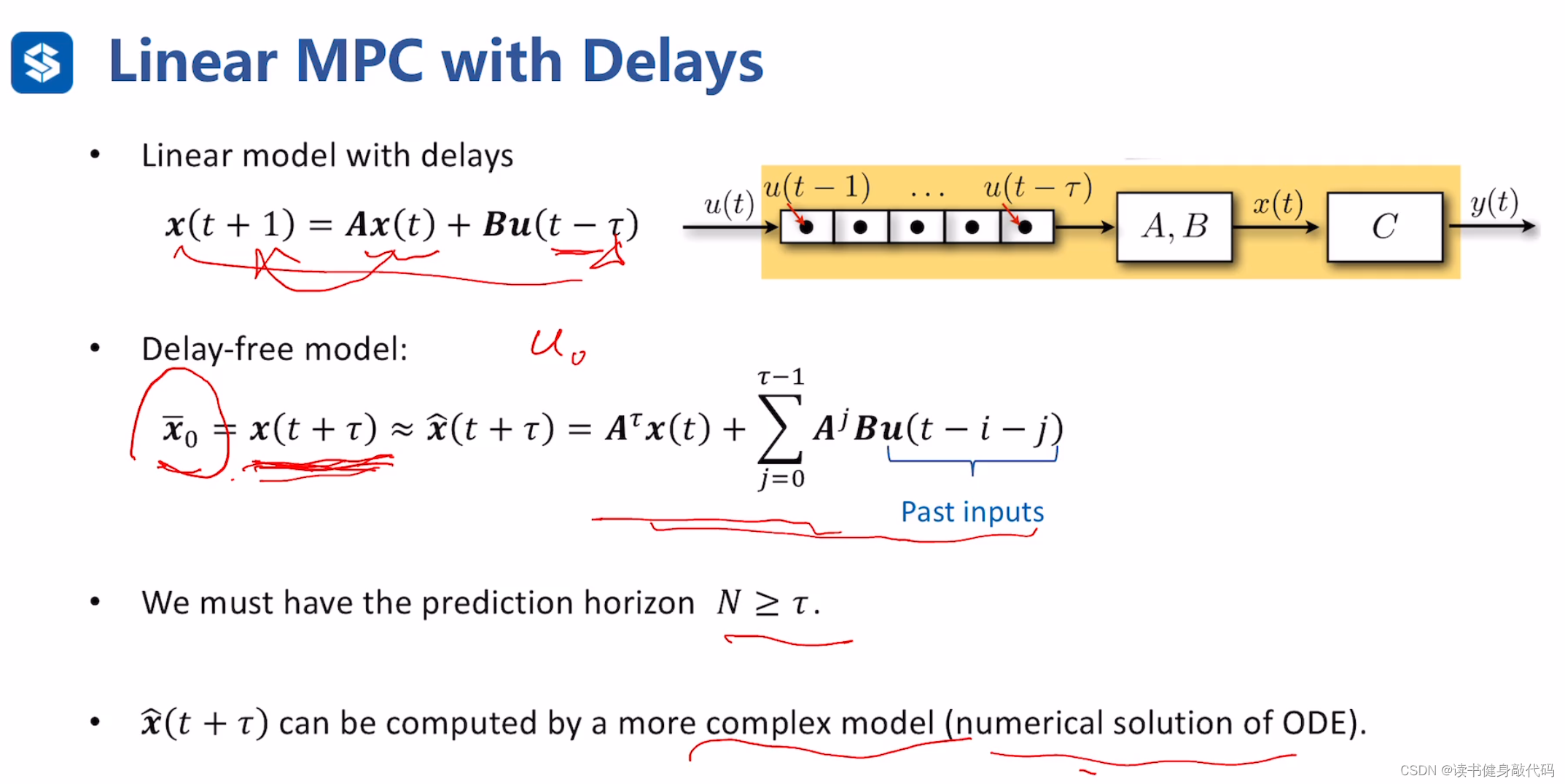
在这里插入图片描述
考虑系统延迟，未来的状态至于现在状态和过去输入有关，与当前输入无关，考虑延迟不仅仅适用于linear MPC，也适用于其他MPC，这里提一下，仅做了解。

在这里插入图片描述

目标函数式二次型，且约束为线性约束的问题称为二次规划问题QP（可回顾上一章博客3.4.1节对凸优化问题的介绍），上图给出了一些常用的QP求解器。

3.3 Other MPC methods

3.3.1 Explict MPC显式MPC(多用于有约束线性MPC)

在这里插入图片描述

无约束的MPC可以推出闭式解batch solution，而有约束的MPC无法推出，只能使用QP求解器进行在线求解。

显式MPC思想：按照初始状态落在不同的区间内提前算好闭式解，使用时查表。

在这里插入图片描述
对于优化问题，如果是等式约束，可以使用Lagrange乘子法求解，对于不等式约束求极值，使用KKT条件求解。

KKT（Karush-Kuhn-Tucker）条件是数学优化领域的一组非常重要的条件，主要用于非线性规划问题的最优解判定。KKT条件是对线性规划中的单纯形方法和对偶理论在非线性情况下的推广。

在一个有约束的优化问题中，如果目标函数和不等式约束是连续可微的，那么在某些正则性条件下，任何局部最优解都必须满足KKT条件。这些条件包括：

梯度条件：目标函数的梯度必须可以表示为各个约束函数梯度的线性组合。
原始可行条件：解必须满足问题中所有的约束。
对偶可行条件：涉及拉格朗日乘子的不等式必须非负。
互补松弛条件：拉格朗日乘子与相应的不等式约束的乘积应该为零。

这些条件在求解实际问题时非常有用，特别是在工程设计、经济学和运筹学中。对于某些优化问题，只要找到满足KKT条件的点，就能确定它是问题的局部最优解，有时甚至是全局最优解。KKT条件是非线性规划领域的基石之一，对于理论研究和实际应用都有极其重要的意义。

GPT4分析：

对于给出的优化问题，我们有目标函数 ( $\frac{1}{2} z^2$ ) 和约束条件 ( $\leq 1 + 3x$ )。要列出这个问题的KKT条件，我们首先需要构造拉格朗日函数 ( $\lambda)$ )，其中 ( $\lambda$ ) 是拉格朗日乘子。

拉格朗日函数为：
$\lambda) = J(z, x) + \lambda (1 + 3x - z)$ $\lambda) = \frac{1}{2} z^2 + \lambda (1 + 3x - z)$

接下来我们根据KKT条件列出：

梯度条件（stationarity）: 解必须使拉格朗日函数的梯度为零。对 ( $z$ ) 和 ( $\lambda$ ) 分别求偏导，我们得到：
$\frac{\partial L}{\partial z} = z - \lambda = 0$ $\frac{\partial L}{\partial \lambda} = 1 + 3x - z = 0$
原始可行性（primal feasibility）: 解必须满足原始问题的约束。
$\leq 0$
对偶可行性（dual feasibility）: 拉格朗日乘子对于不等式约束必须非负。
$\lambda \geq 0$
互补松弛性（complementary slackness）: 对于每个乘子和对应约束的乘积为零。
$\lambda (z - (1 + 3x)) = 0$

将第一个梯度条件 ( $\lambda = 0$ ) 代入互补松弛性的条件，我们得到：
$\lambda (z - (1 + 3x)) = \lambda z - \lambda (1 + 3x) = 0$
由于 ( $\lambda$ )，这可以简化为：
$\lambda^2 - \lambda (1 + 3x) = 0$ $\lambda (\lambda - (1 + 3x)) = 0$

这意味着要么 ( $\lambda = 0$ )，要么 ( $\lambda = 1 + 3x$ )。根据对偶可行性的规则，我们知道 ( $\lambda$ ) 必须非负，因此
( $\lambda = 0$ ) 或者 ( $\lambda$ ) 是一个非负值。

当 $\lambda=0$ 时，z=0
当 $\lambda>0$ 时， $z = 3 x + 1 > 0$

即可得出上图中满足约束时的J的曲线。

可以证明，对于一个严格凸的QP，其多参数优化的解是连续分段线性的。

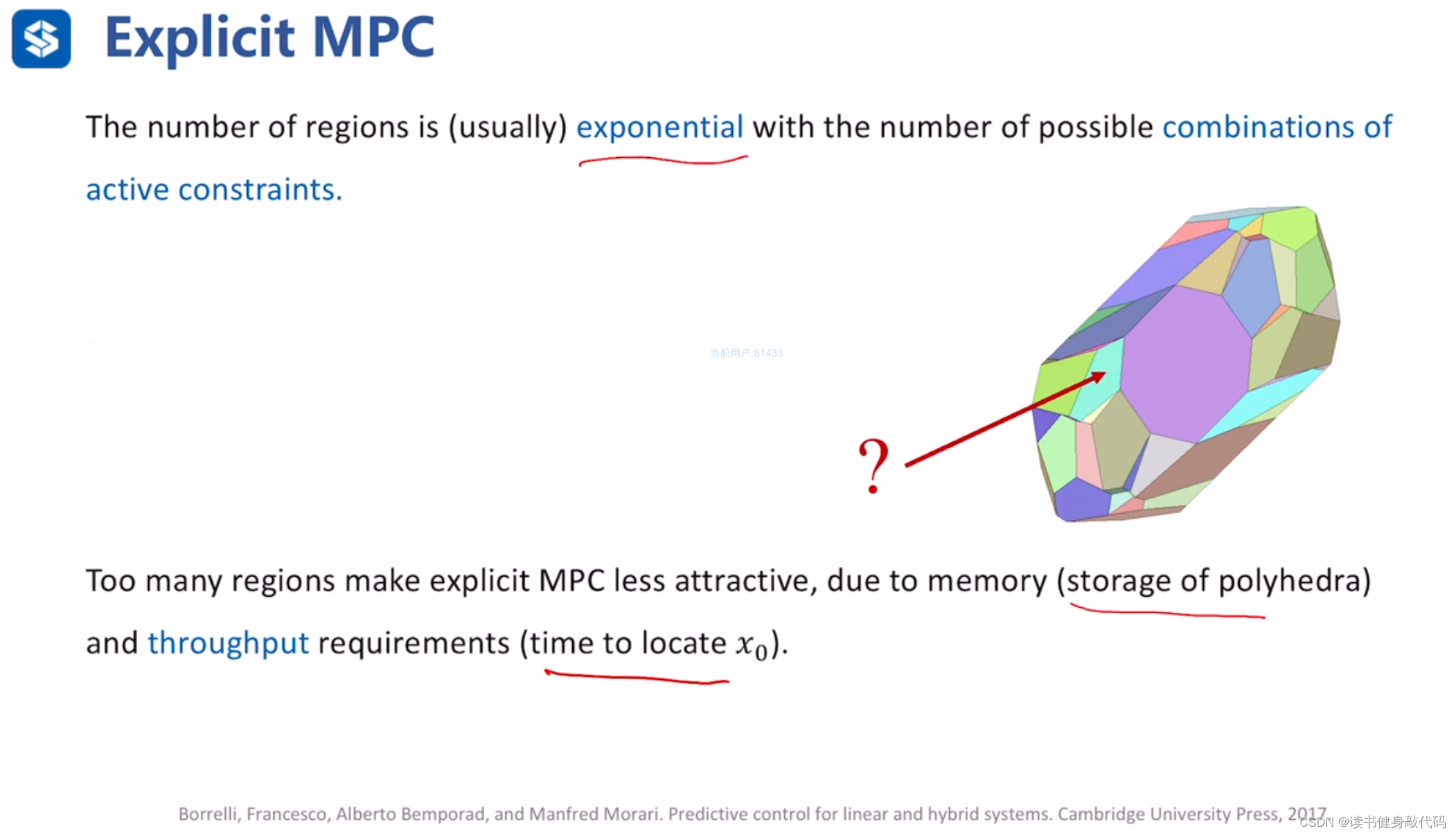
在这里插入图片描述
Explicit MPC根据状态的区间个数来计算最优解，但问题是区间的个数与有效约束的个数呈指数级增长，存储和查找区间的代价非常高昂。所以Explicit MPC多用于自动化控制，而在Robotics领域很少使用。

3.3.2 Linear Time-Varying MPC and Nonlinear MPC(线性时变MPC和非线性MPC)

3.3.2.1 Linear Time-Varying MPC

在这里插入图片描述
线性时变模型：典型的线性时变系统是火箭动力，随着火箭的上升，消耗的燃料增加，质量减少，系统方程随着时间发生改变。

非线性模型：系统方程无法线性表示。处理方法一般是对非线性模型进行线性化（如一阶Taylor展开，然后对线性化的模型进行处理），由于线性化点不同，不同时刻的系统方程也不同，所以也是时变系统。

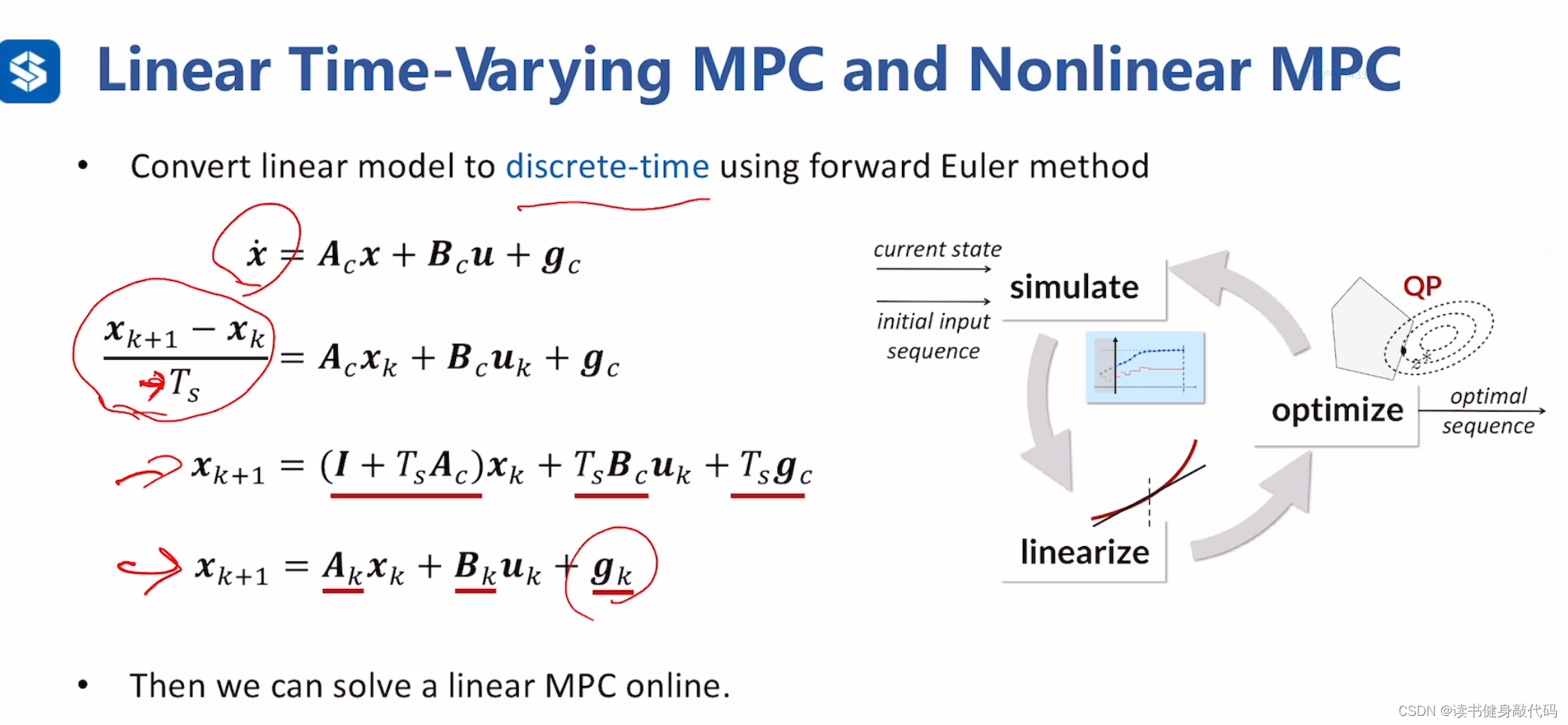
在这里插入图片描述
线性化之后进行离散化，得到离散的线性化MPC模型，从而在线求解。

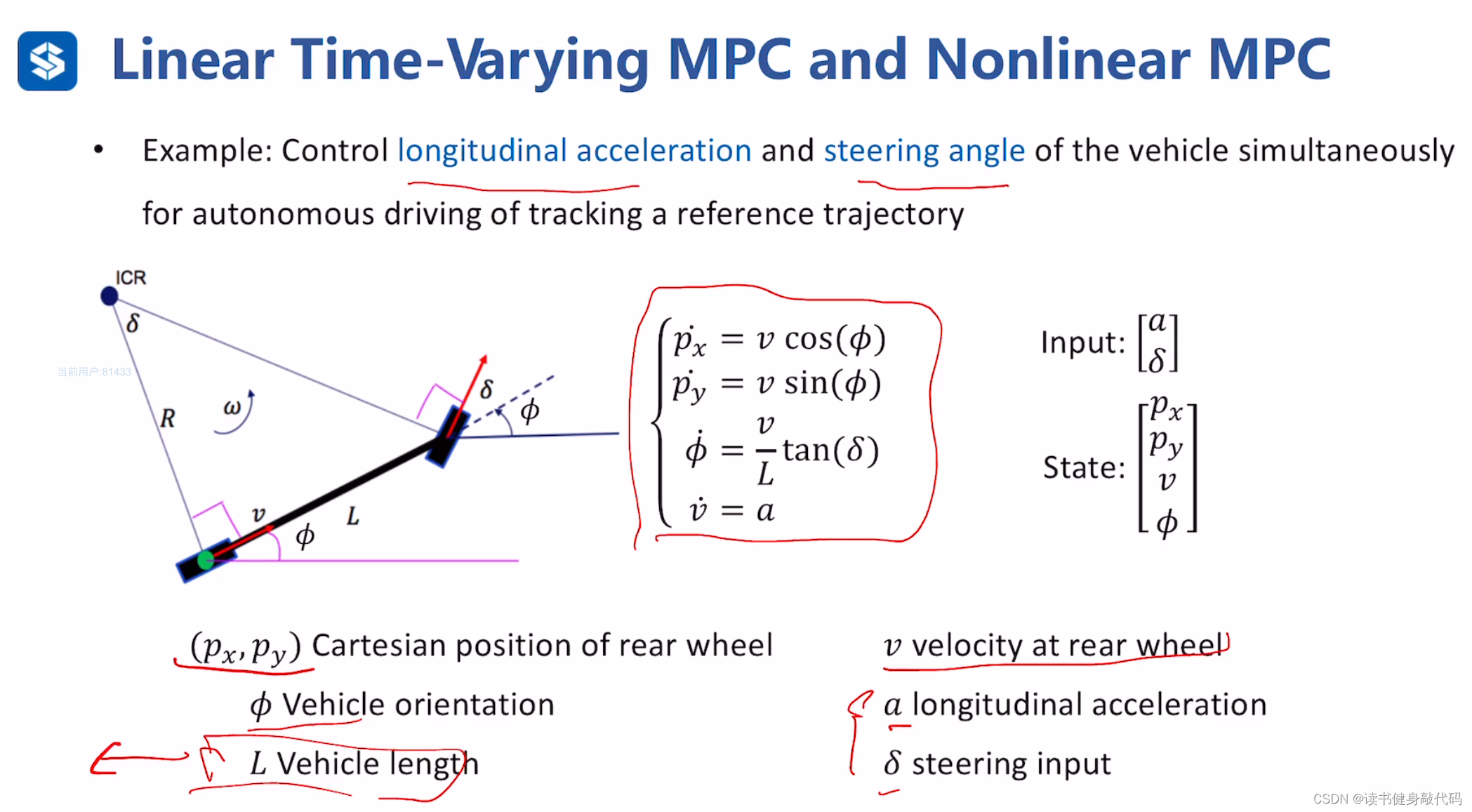
在这里插入图片描述
图为自行车模型，通过状态转移方程可知系统为非线性时变系统。

上述推导，使用了一阶泰勒展开，以 $\dot{p_x}$ 为例，简要推导。
Taylor公式，展开点为 $x_0$ ：
$f(x)=f(x_0)+\frac{f^{(1)}(x_0)}{1!}(x-x_0)+\frac{f^{(2)}(x_0)}{2!}(x-x_0)^2\cdots$

取第一阶导进行线性化，忽略高阶导，在 $(\bar{v},\bar{\phi},\bar{\delta})$ 处进行展开，则
$\begin{align*} \dot{p(x)} &=\bar{v}cos(\bar{\phi})+\frac{\partial(\dot{p_x})}{\partial v}(v-\bar{v})+ \frac{\partial(\dot{p_x})}{\partial \phi}(\phi-\bar{\phi}) \notag \\ &=\bar{v}cos(\bar{\phi})+cos(\bar{\phi})(v-\bar{v})-\bar{v}sin(\bar{\phi})(\phi-\bar{\phi})\\ &=cos(\bar{\phi})v-\bar{v}sin(\bar{\phi})(\phi-\bar{\phi}) \end{align*}$ 但是在对 $\dot{p_x}$ 进行整理时，我的结果为
$\dot{p_x}= \begin{bmatrix} 0 &0&cos(\bar{\phi})&-\bar{v}sin(\bar{\phi}) \end{bmatrix} \begin{bmatrix} p_x\\p_y\\v\\ \phi \end{bmatrix} + \begin{bmatrix} 0&0 \end{bmatrix} \begin{bmatrix} a\\\delta \end{bmatrix} + \begin{bmatrix} \bar{v}\bar{\phi}sin(\bar{\phi}) \end{bmatrix}$
与课程所给的结果有出入，但是整体推导思路应该没错。

在这里插入图片描述
线性化之后，进行离散化。

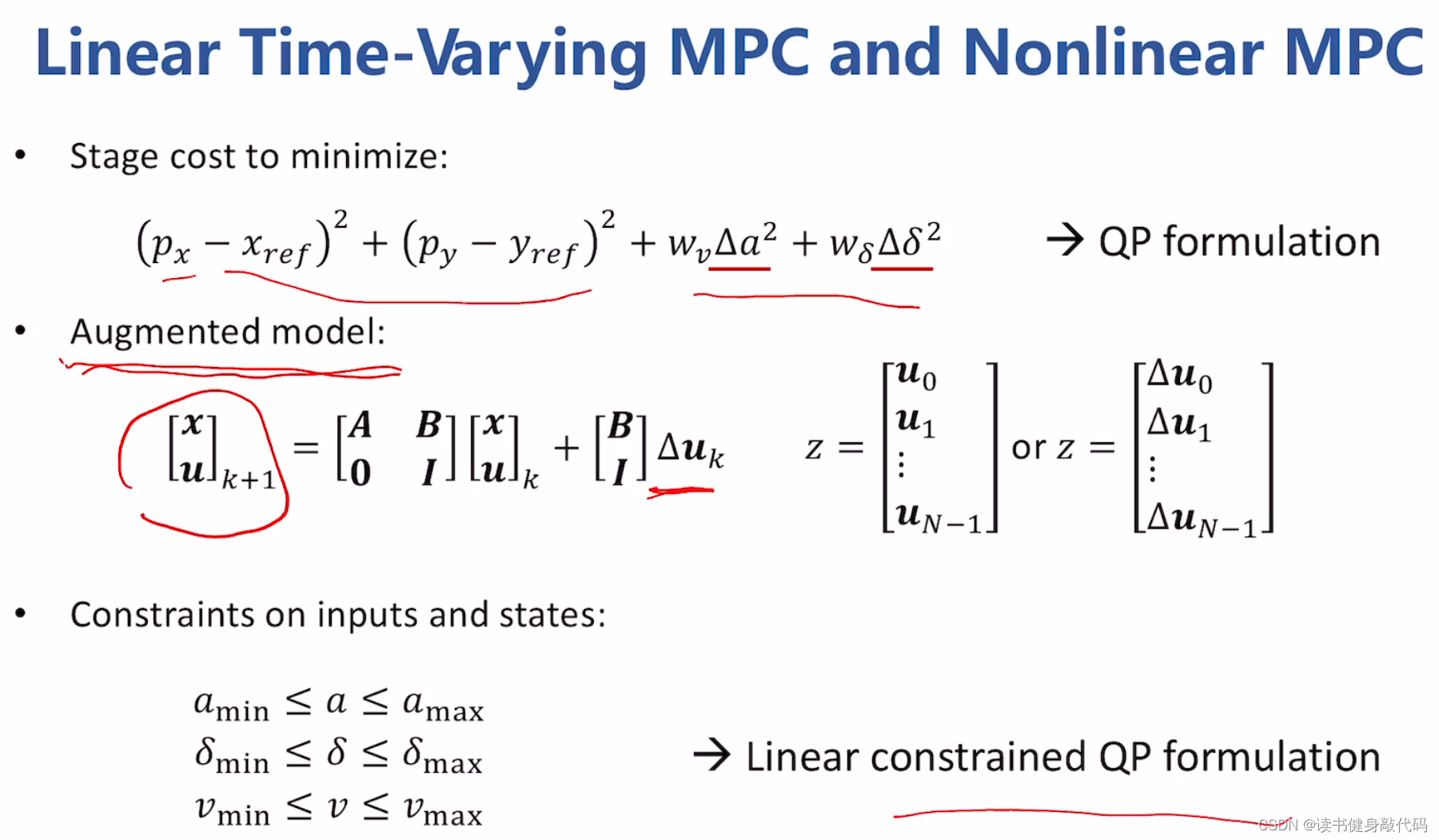
在这里插入图片描述
回到问题的cost function，由两部分组成：最小化轨迹跟踪误差；对轨迹进行smooth，使变化率不会太大。

有一个模型的技巧，称为Augmented model，把系统的新的状态量 $x_{k+1}$ 和输入 $u_{k+1}$ 当做新状态，把输入量的增量 $\Delta {u_k}$ 当做新的输入（有点类似增量式PID的思想，控制比例，积分，微分的增量，而不是绝对量。）

最后，读输入和状态进行约束，交给求解器求解。

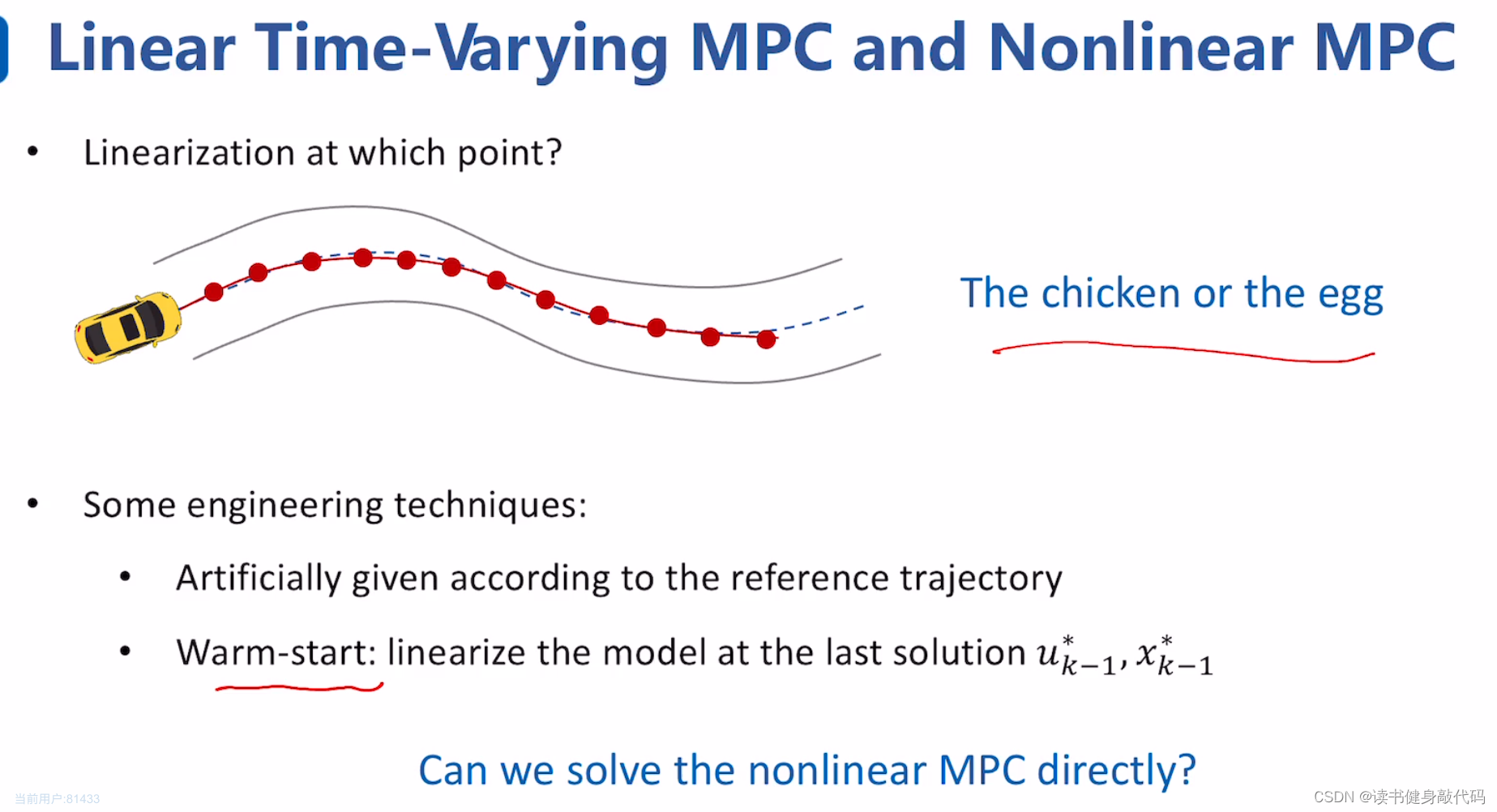
在这里插入图片描述
这里比较重要的一点是线性化点如何给定，如果知道了线性化点，那就没有必要进行求解了，输入先有鸡还是先有蛋的问题(The chicken or the egg)

给线性化点有一些工程上的策略：

根据参考轨迹给出。
warm-start：使用 $k - 1$ 时刻的解( $u_{k-1}^*,x_{k-1}^*$ )来作为 $k$ 时刻线性化的点(会不会出现SLAM中的线性化点不同而导致的解零空间的退化问题，那里是因为Jacobian的线性化点不同会导致Jacobian在被marg掉的点处不再发生变化，导致information matrix中多加了信息，有可能改变解的零空间。有类似于EFJ算法来解决这个问题。)

3.3.2.2 Nonlinear MPC

在这里插入图片描述
非线性可以由cost funtion、系统方程、约束带来。

前面讲解了对非线性优化问题进行线性化、离散化求解，也可以直接对非线性优化进行求解，即求解NLP，但是后者难度更大，因为QP问题是凸的，local munimum就是global minimum，而非凸NLP的local minimum不一定是global minimum。

一些NLP求解方法：

SQP
内点法

求解非线性MPC(即NMPC)有FORCES Pro，可以基于MATLAB代码生成C代码。

3.3.3 Tube MPC（抗扰动）

在这里插入图片描述
非线性MPC难点：

系统辨识难（通常是对系统参数进行辨识）
迭代求解的可行性和稳定性无法保证（可能求着求着就无解了）

提出一种方法：Tube MPC。具体思路是：MPC+反应式控制器。MPC使用nominal model（名义模型，标称模型），后面接上一个反应式控制器，使得实际的状态收敛到MPC规划出的名义的管道内(nominal tube)。这里MPC实际上是一个规划器，后面的feedback controller才是控制器，一个辅助反馈控制器，其目的是保持实际状态在忽略干扰计算出的名义轨迹周围的一个不变的“管”内。

所以Tube MPC本身就具有一定的抗干扰能力，常用于鲁棒控制。

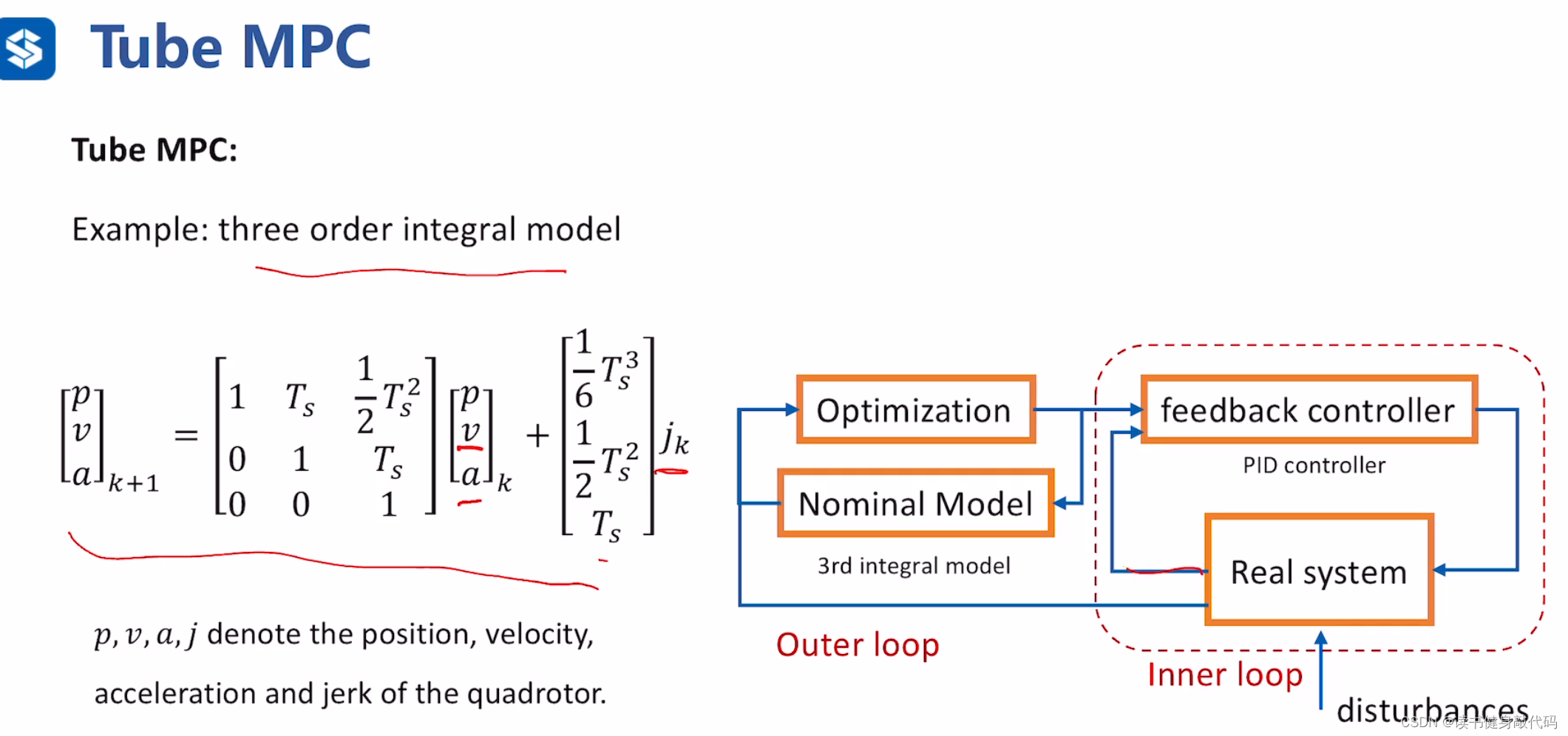
在这里插入图片描述

例子：名义模型使用了三积分模型（以jerk作为系统输入），feedback controller使用了PID控制器。
整个控制框架很像串级控制。内外环的反馈均使用了真实的系统测量。

3.3.4 Hybrid MPC（混合MPC）

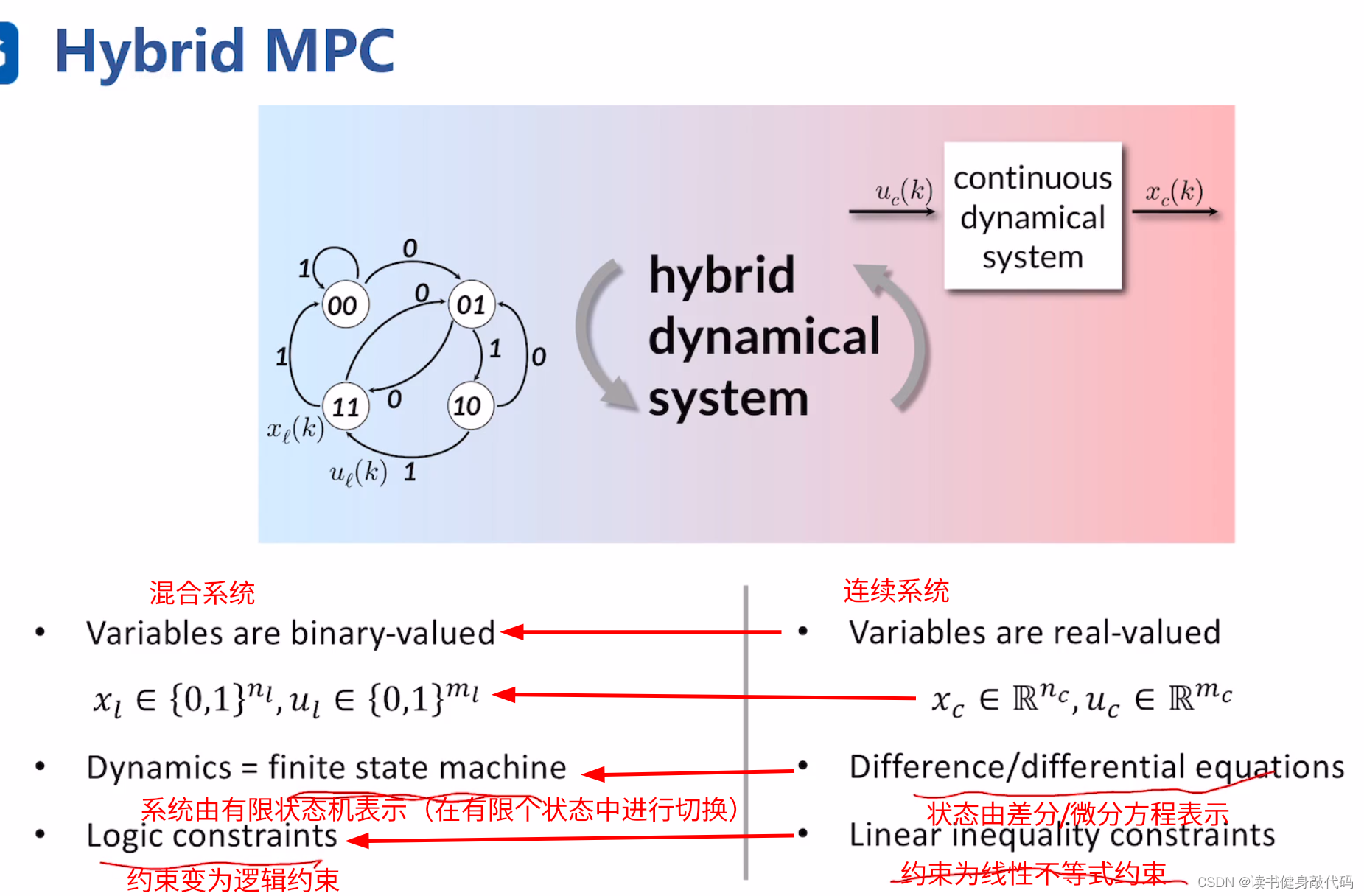
在这里插入图片描述
主要指系统的状态和约束由“连续” 变为 “连续 + 逻辑”混合。

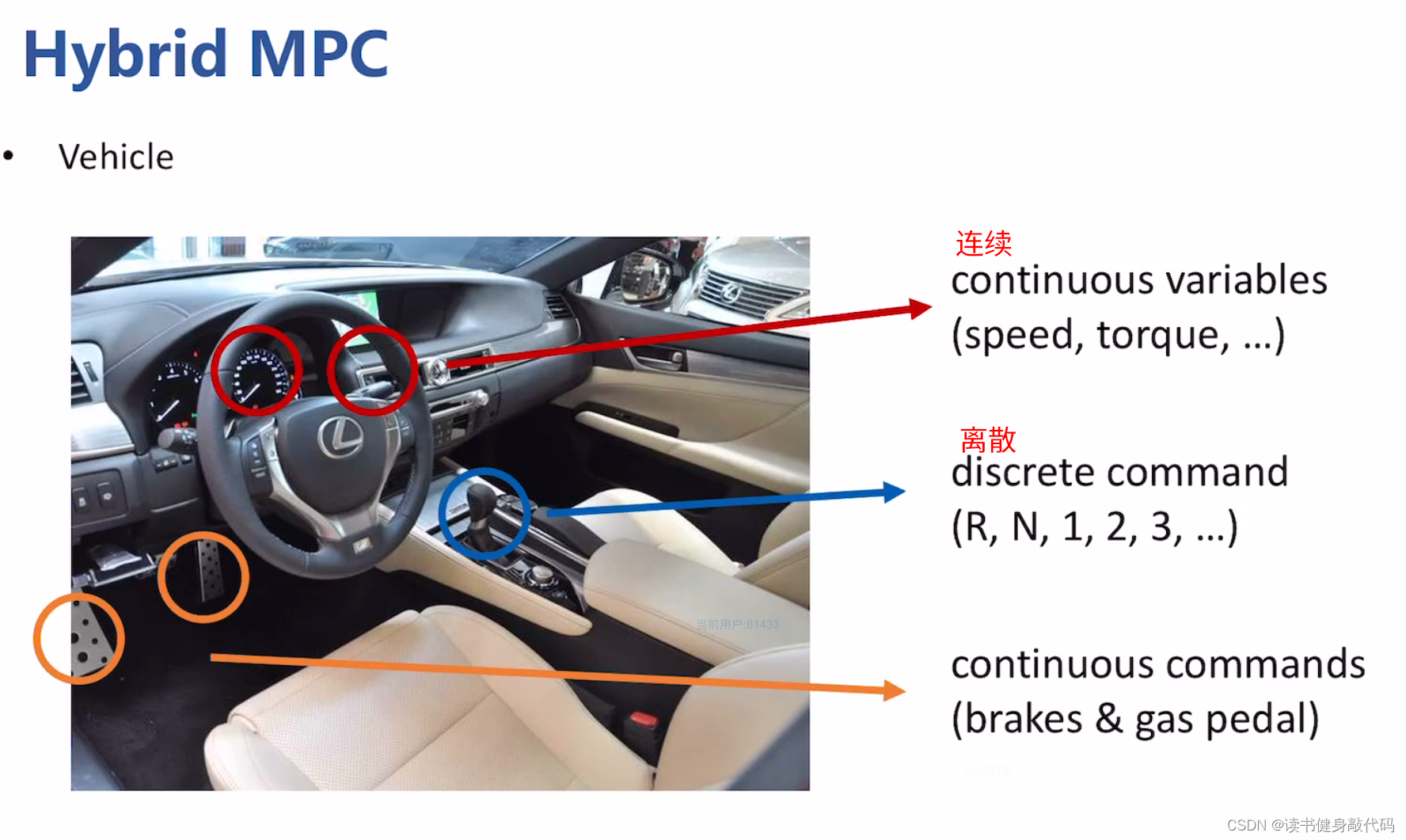
汽车就是连续+逻辑的混合系统。

在连续动态系统中混合着逻辑变量或约束的系统称为混合逻辑动态(MLD)系统
这里 $\leq 0$ 表示的是反弹的过程，实际 $y$ 不可能小于0，但用符号来代表不同的运动过程。
简言之， $y > 0$ 表示下落， $y\leq 0$ 表示反弹，将这种逻辑约束用含有逻辑变量 $\delta$ 的不等式进行表示
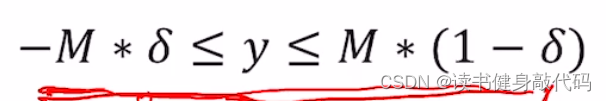
在这里插入图片描述
速度转移方程可如下表示：

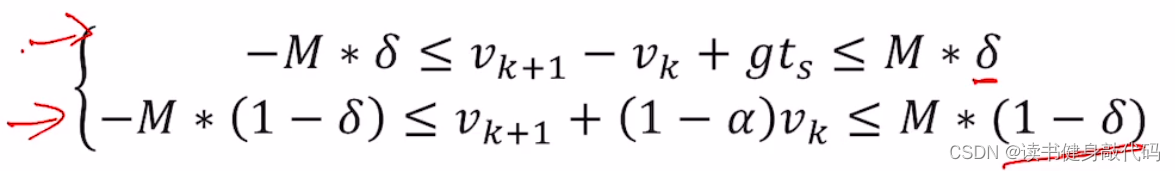
在这里插入图片描述
将逻辑约束转换为混合整数线性不等式，就能使用线性/非线性方法求解。

上图为一个无人机拉重物的例子，物体对无人机的拉力 $T$ ，在绳子紧绷时等于 $m_La$ ，松弛时 $T = 0$
$T$ 为无人机推力， $q$ 为无人机相对重物(load)方向， $m_L$ 为重物质量， $\ddot{p_L}$ 为重物位置的二阶导，即加速度， $l$ 为无人机距离重物距离， $l_0$ 为绳长(假设身子为刚性，无形变)。

第二个式子表示当 $l$ 小于绳长时，拉力就为0。

3.3.5 MPCC（模型预测轮廓控制）

GPT4：
模型预测轮廓控制（Model Predictive Contouring Control，简称 MPCC）是一种先进的控制策略，它是模型预测控制（Model Predictive Control，MPC）的一个变体，专门用于控制系统在保持特定轨迹或轮廓精度方面的性能。

模型预测控制是一种基于模型的控制算法，能够考虑系统的未来行为，并在每一个控制步骤中解决一个优化问题，以确定当前的最优控制动作。MPC的这个特点使得它非常适合处理多变量系统、受约束的系统和非线性系统。

MPCC特别关注于在给定的轨迹或轮廓上实现高精度跟踪，这在很多工业应用中非常重要，比如机器人路径跟踪、CNC机床加工和汽车路径跟踪等。MPCC不仅考虑系统的动态和可能的约束，而且还将轨迹跟踪误差最小化作为关键的优化目标。它通常可以分为两个主要部分：轨迹规划和轨迹跟踪。

轨迹规划负责生成理想的、可执行的路径或轮廓，而轨迹跟踪则确保控制系统能够尽可能精确地跟随这个路径。MPCC通过在线优化实时控制输入，不仅可以减少轨迹偏差，还可以应对外部扰动，从而保证系统沿着预定轨迹高精度运行。

MPCC的实施通常需要强大的计算能力，因为它需要在实时或准实时条件下解决优化问题。随着计算技术的发展，MPCC已经成为许多高精度和高性能控制应用的首选方法。

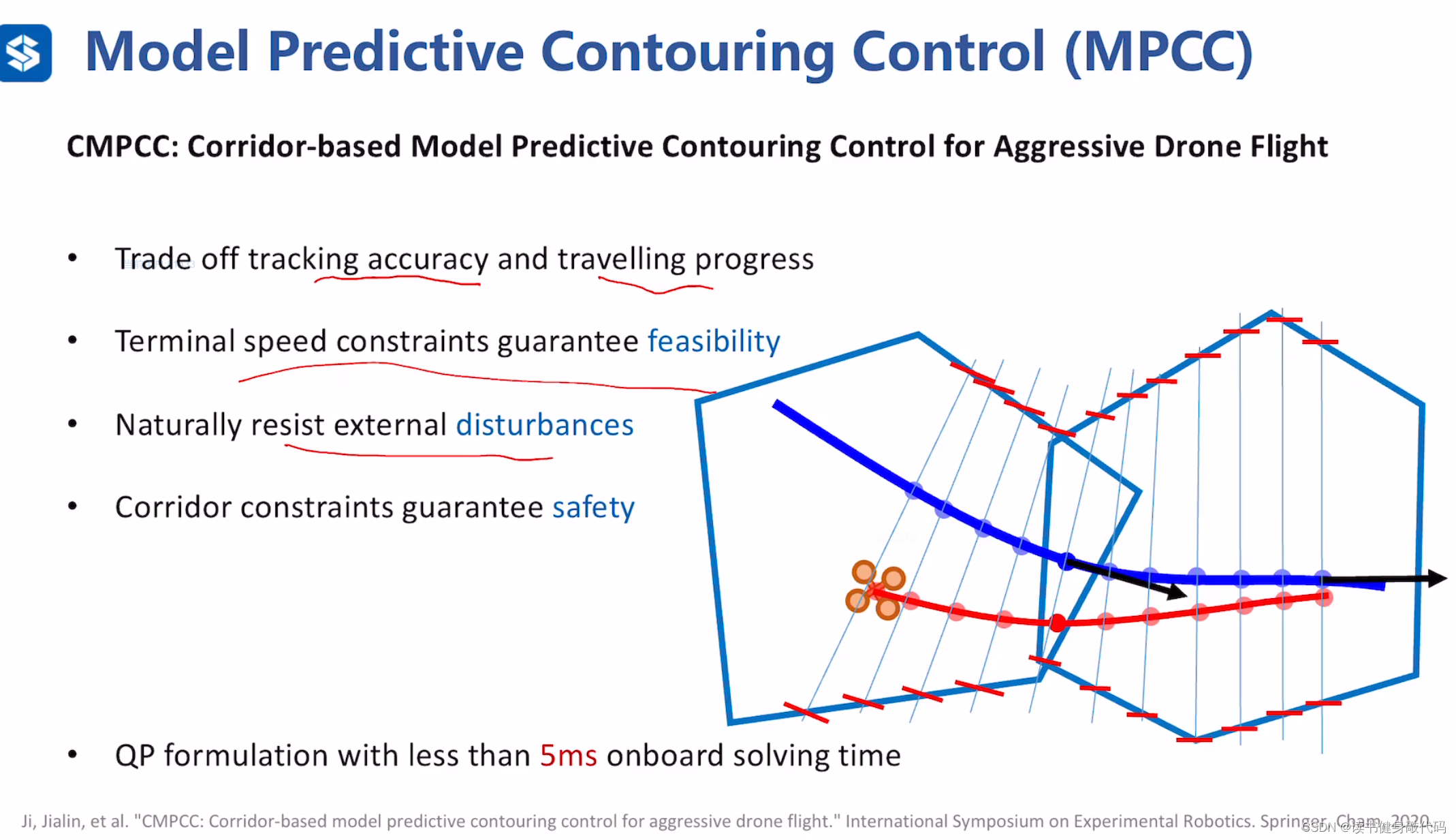
在这里插入图片描述

把MPCC应用在无人机的抗扰动鲁棒飞行中(讲师工作ref[8])。
Contribution：

是精度和跟踪速度的trade-off
用末端轨迹速度约束来保证可行性(末端速度小于参考轨迹的速度)
使用tube MPC抗扰动
使用flight corridor保证飞行的安全性

任务是跟踪一个小球的轨迹。

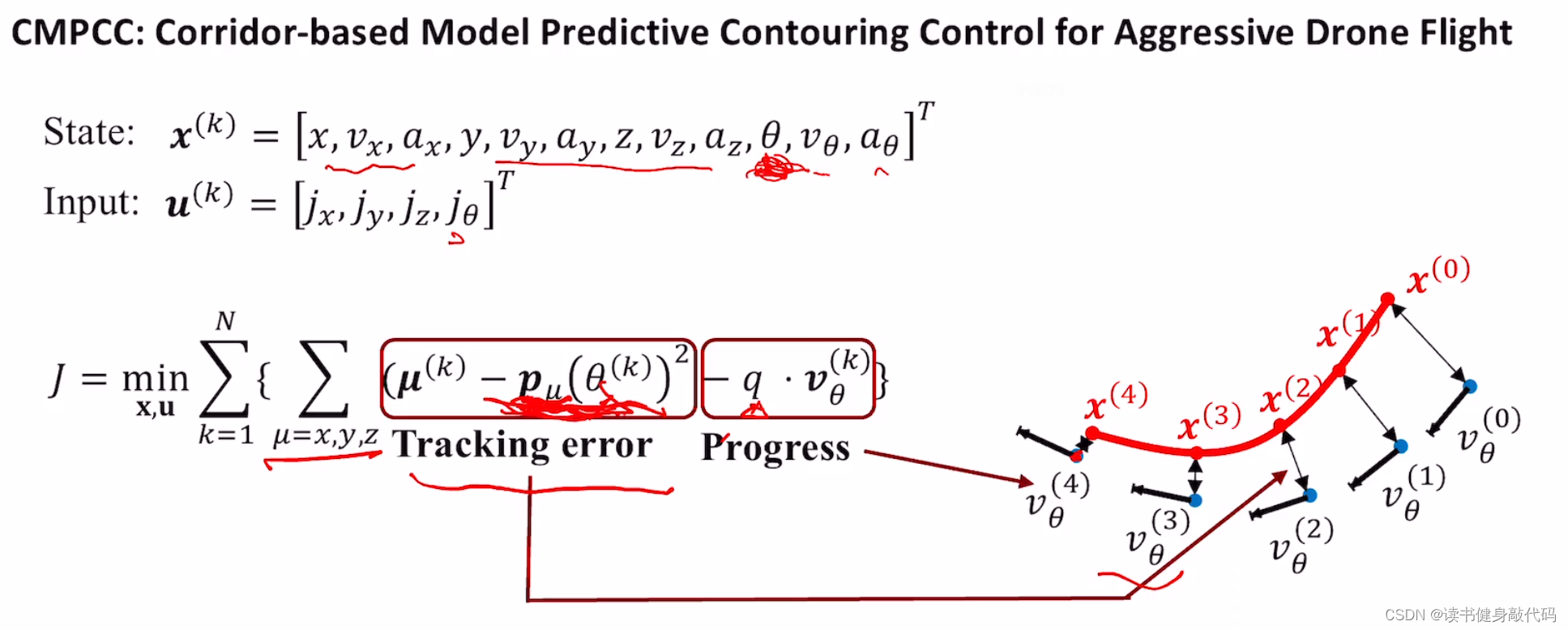
在这里插入图片描述
把非时变MPC转化为线性时变MPC。

$\theta$ 表示跟踪的小球的位置，输入是无人机的jerk和小球的jerk

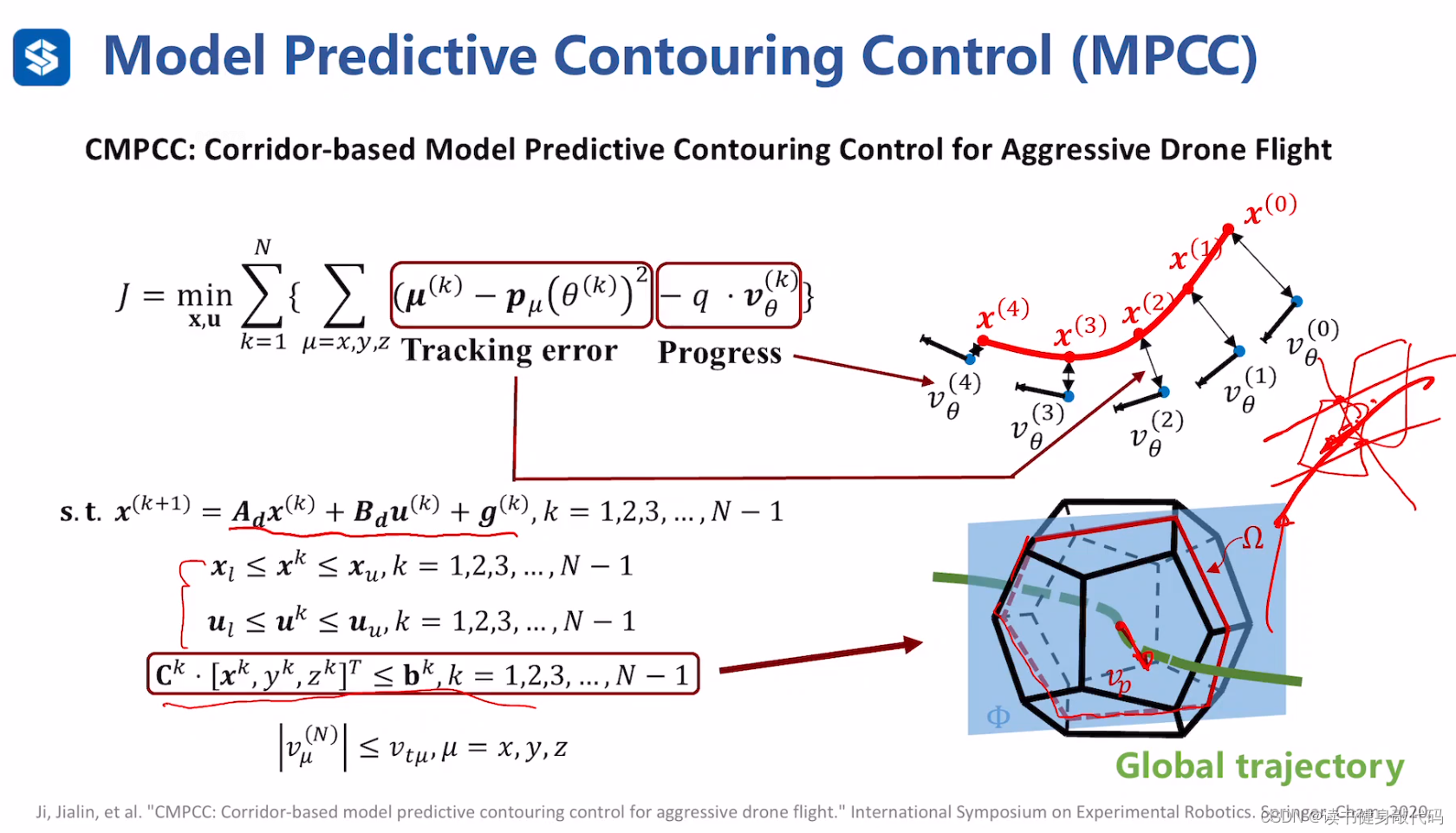
在这里插入图片描述
$-q\cdot v_{\theta}$ 项是最大化跟踪进度(不是很理解)，
约束：
第一行：系统线性化，离散化
第二、三行：状态和输入的最值约束
第四行：安全约束，使用flight corridor，但由于优化过程中对处于两个flight corridor间的轨迹不知道属于哪个corridor，不知如何优化，处理方法是：做该点速度方向的法平面，与flight corridor相较，沿着速度方向向外拉，与flight corridor组成的平面就作为安全约束（不是很清楚，需要看论文）。

算法效果如下：
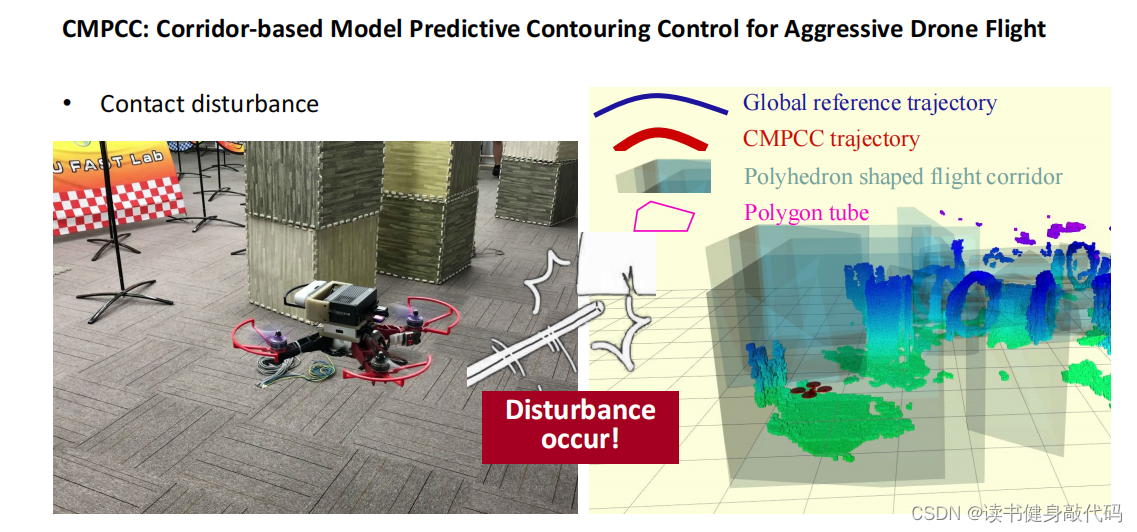
在这里插入图片描述
飞行过程中遭遇打击也能正常飞行。

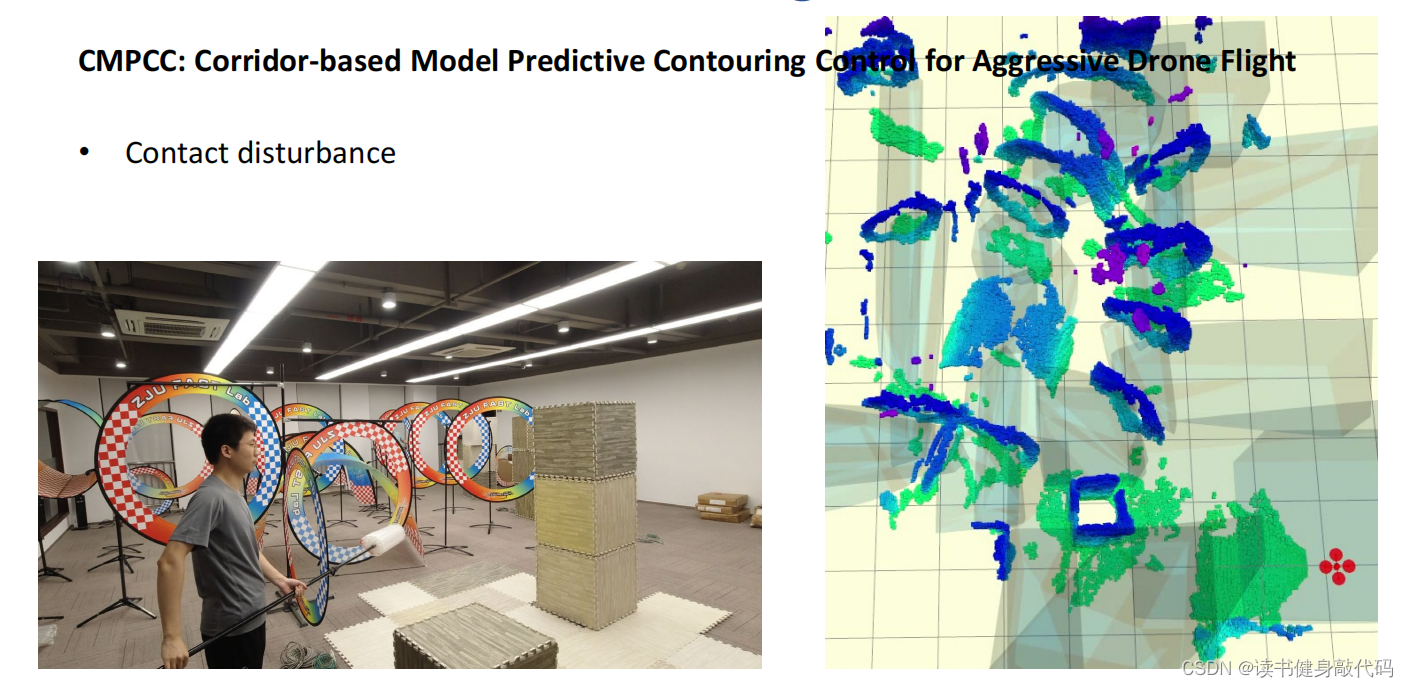
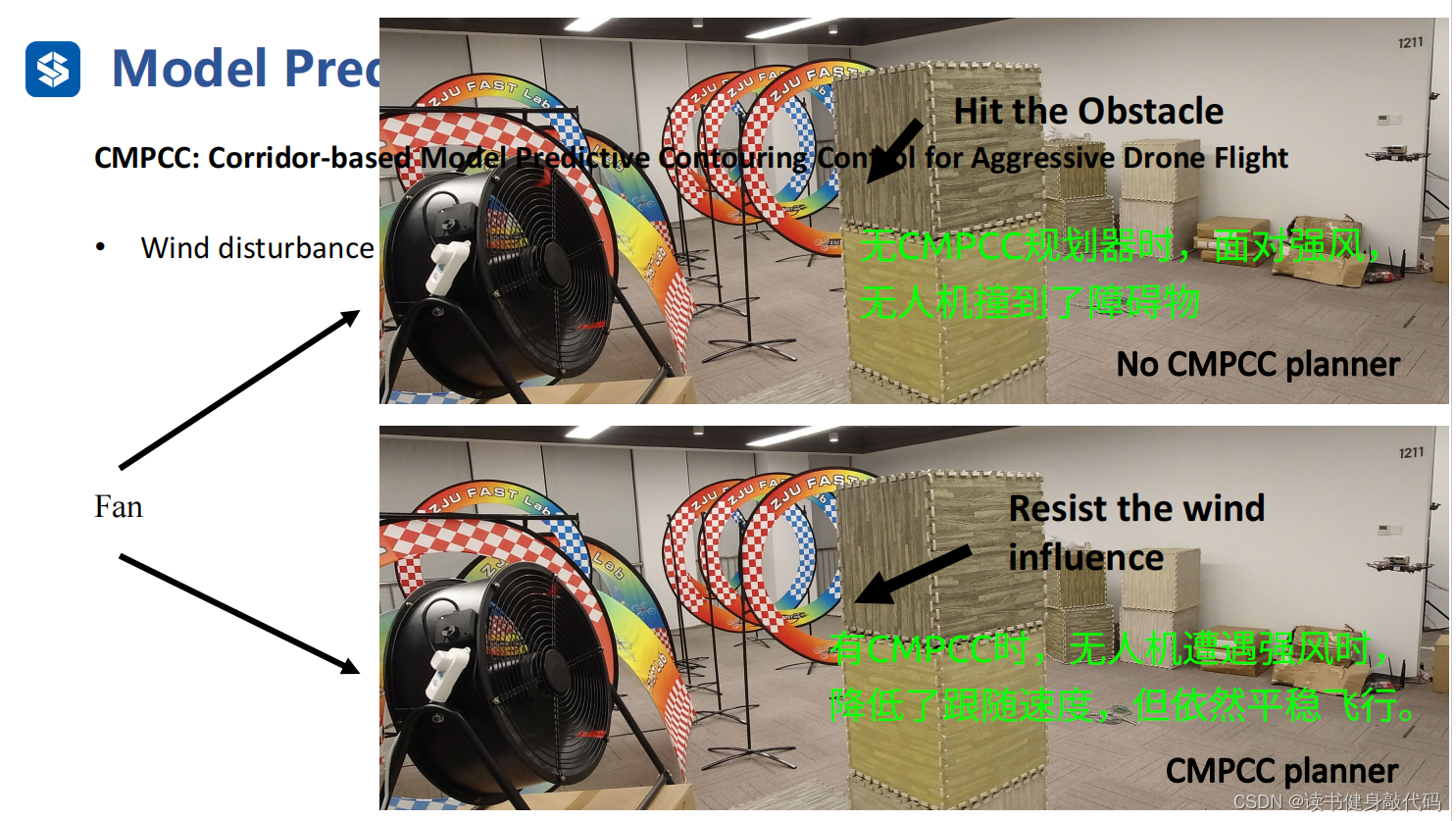
在这里插入图片描述

4. Summary

在这里插入图片描述

Reactive Control & Optimal Control
reactive control能使用误差信息，但无法处理具有耦合关系的约束等，optimal control处理了约束问题，但无法解决长时间控制问题，且没考虑扰动问题。
Model Predictive Control：
与最优控制不同，MPC只预测一小段的轨迹，然后只执行一部分，然后根据measurements继续执行预测，控制，测量的循环。
MPC pros：1. 能够考虑未来的信息(相对最优控制而言)，2. 补偿误差，3. 减小问题的规模。
MPC design：
1. 预测模型的选择：是求解精读和复杂性的trade-off，ref [5,6]
2. MPC cost funtion设计：不同要求会有不同的参数设计
3. 预测时长PH：最优控制的预测时长是整段轨迹时长，而MPC只针对一小段轨迹。recursive feasiability：虽然只优化一小段，但是保证问题一定有解，常见实现方法是给PH终点的末状态增加约束。(在ref[8]中有所提及)
Linear MPC (unconstrained and constrained case)
- unconstrained case可以推导出closed-form solution：
  1. condensed batch solution，但是求逆较慢， $O(n^3)$ 。
  2. non-condenced MPC，会引入新的约束，不常用。
- LQR：鉴于condensed batch solution $O(n^3)$ 的复杂度，针对二次规划问题，提出LQR方法，使用Bellman princlple，最优解的对应部分仍然是子问题的最优解，从后往前一步步推导，直至推导完整个问题的最优解。但仅适用于cost function为二次型情况。
有约束情况在explicit MPC开始考虑，使用KKT条件添加约束。
MPC with delays
考虑系统延迟，未来的状态至于现在状态和过去输入有关，与当前输入无关，考虑延迟不仅仅适用于linear MPC，也适用于其他MPC。
Explicit MPC
针对有约束MPC，无约束的MPC可以推出闭式解batch solution，而有约束的MPC无法推出。

等式约束一般使用Langrange乘子法构建问题，不等式约束一般使用KKT条件构建问题。

我们简述了KKT条件：1.梯度条件；2. 原始可行条件；3. 对偶可行条件；4.互补松弛条件。

并在3.3.1节举例说明。

对于Explicit MPC：
1. 显式MPC思想：按照初始状态落在不同的区间内提前算好闭式解，使用时查表。
2. 缺点：根据状态的区间个数来计算最优解，但问题是区间的个数与有效约束的个数呈指数级增长，存储和查找区间的代价非常高昂。故Explicit MPC仅常用于自动控制领域，robotics领域不常用。
Linear Time-Varying MPC and Nonlinear MPC
针对非线性系统，可对系统进行线性化近似(一阶泰勒展开)，并离散化，转化为线性时变系统求解。

关于线性化点的给定，给出两个策略：1. 根据参考轨迹给出。2. warm-start，使用 $k - 1$ 时刻的解作为 $k$ 时刻的线性化点。
Tube MPC
非线性MPC难点：
1. 系统辨识难（通常是对系统参数进行辨识）。
2. 迭代求解的可行性和稳定性无法保证（可能求着求着就无解了）。
提出 Tube MPC。具体思路是：MPC+反应式控制器。MPC使用nominal model（名义模型，标称模型），通常是做规划器，反应式控制器实施控制，使输出维持在nominal trajectory的tube内，提高预测控制稳定性。
Hybrid MPC
hybrid MPC对于逻辑量，将其处理为混合整数或互补约束。
Model Predictive Contouring Control
一种具体算法，用于轮廓控制，具体可参考ref[8]，添加了末端速度约束以保证feasiability，使用Tube MPC增加了控制鲁棒性。

5. Assignment

在这里插入图片描述
给出一些拓展学习资料：
ref[9]，youtube学习MPC的一个视频。

ref[10]一个MPC课程网站，IMT School for Advanced Studies Lucca（意大利卢卡高级研究学院）一位老师做的。

ref[2]一本讲预测控制的书，前几章包含一些优化的数学知识。

6. Reference

[1] Mellinger, Daniel, and Vijay Kumar. “Minimum snap trajectory generation and control for quadrotors.” 2011 IEEE international conference on robotics and automation. IEEE, 2011.

[2] Borrelli, Francesco, Alberto Bemporad, and Manfred Morari. Predictive control for linear and hybrid systems. Cambridge University Press, 2017.

[3] Nan, Fang, et al. “Nonlinear MPC for Quadrotor Fault-Tolerant Control.” arXiv preprint arXiv:2109.12886 (2021).

[4] Bjelonic, Marko, et al. “Whole-body mpc and online gait sequence generation for wheeled-legged robots.” 2021 IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS). IEEE, 2020.

[5] Kong, Jason, et al. “Kinematic and dynamic vehicle models for autonomous driving control design.” 2015 IEEE intelligent vehicles symposium (IV). IEEE, 2015.

[6] Liniger, Alexander, Alexander Domahidi, and Manfred Morari. “Optimization-based autonomous racing of 1: 43 scale RC cars.” Optimal Control Applications and Methods 36.5 (2015): 628-647.

[7] Wang, Yang, and Stephen Boyd. “Fast model predictive control using online optimization.” IEEE Transactions on control systems technology 18.2 (2009): 267-278.

[8] Ji, Jialin, et al. “CMPCC: Corridor-based model predictive contouring control for aggressive drone flight.” International Symposium on Experimental Robotics. Springer, Cham, 2020.

[9] https://www.youtube.com/watch?v=XaD8Lngfkzk

[10] http://cse.lab.imtlucca.it/~bemporad/mpc_course.html