最近在忙学校官网上的题，就借此记录分享一下有价值的题：

1.注意枚举角度

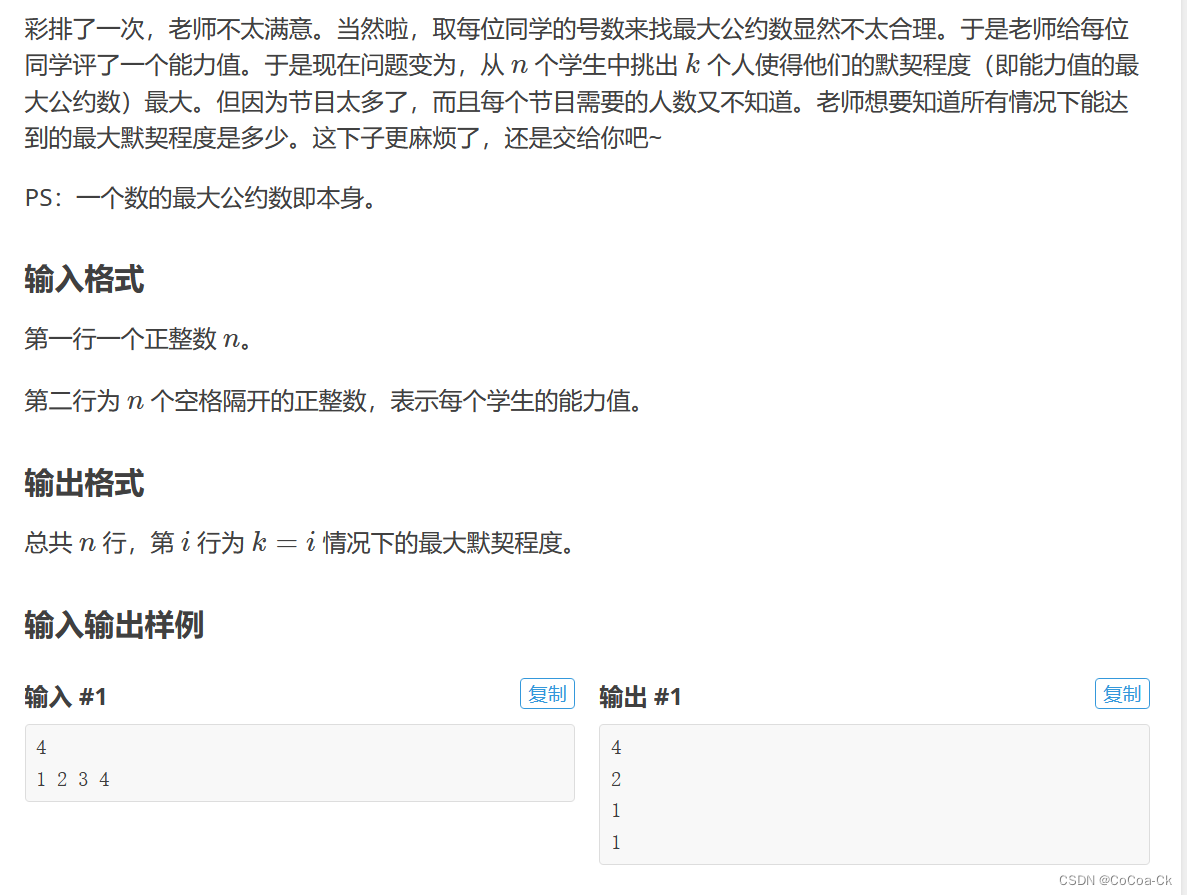
如果我们就对于不同的k常规的枚举，复杂度直接炸了。

于是我们考虑换一个角度，我们不妨从1开始枚举因子，我们记录下他的倍数的个数sum个，

这样子我们就保证了最大gcd至少为他的个数有sum个。

然后我们从k=1开始，倒着输出即可。（这里提供了一种求gcd的新的思路，很有意思）

这里提一下复杂度的问题，外层为n，里面为n/i;

对于学过高数的都知道他约为inn，因此复杂度为nlogn就可以了。

下面是AC代码：

#include<bits/stdc++.h>
using namespace std;
int a[1000010],b[1000010],n,x,max1=-1000000,ans[1005];
int main(){
	cin>>n;
	for(int i=1;i<=n;i++){
		scanf("%d",&x);
		a[x]++;
		max1=max(max1,x);
	}
	for(int i=1;i<=max1;i++){
		for(int j=i;j<=max1;j+=i){
			if(j%i==0) b[i]+=a[j];
		}
	}
	int k=1;
	for(int j=max1;j>=1;j--){
		if(k>n) break;
		if(b[j]>=k){
			k++;
			printf("%d\n",j);
			j++;
			continue;
		}
	}
}

2.注意等效：

首先，对于把n-1个数+1，其实就是等效于指定一个数-1.

然后我们考虑相等时的数是多少。

在这里我们应该还记得带权中位数的概念（前面有讲），我们相当于让这些权1的点走到某一点处总距离min，我们只要求中位数即可。

3.水题

我们把划分两个序列区间看成向两个容器中按顺序添加值。

显然，分值加不加就看最后一个数，我们假设一个容器1最后为a,另一个容器2最后为b.（a>=b)

此时要加进来的为c,如果c>=a,那么加在b后肯定更优。

如果c<=b，那么加在b后肯定更优。

若b<c<a,那么放在a后更优，请看下面的分析：