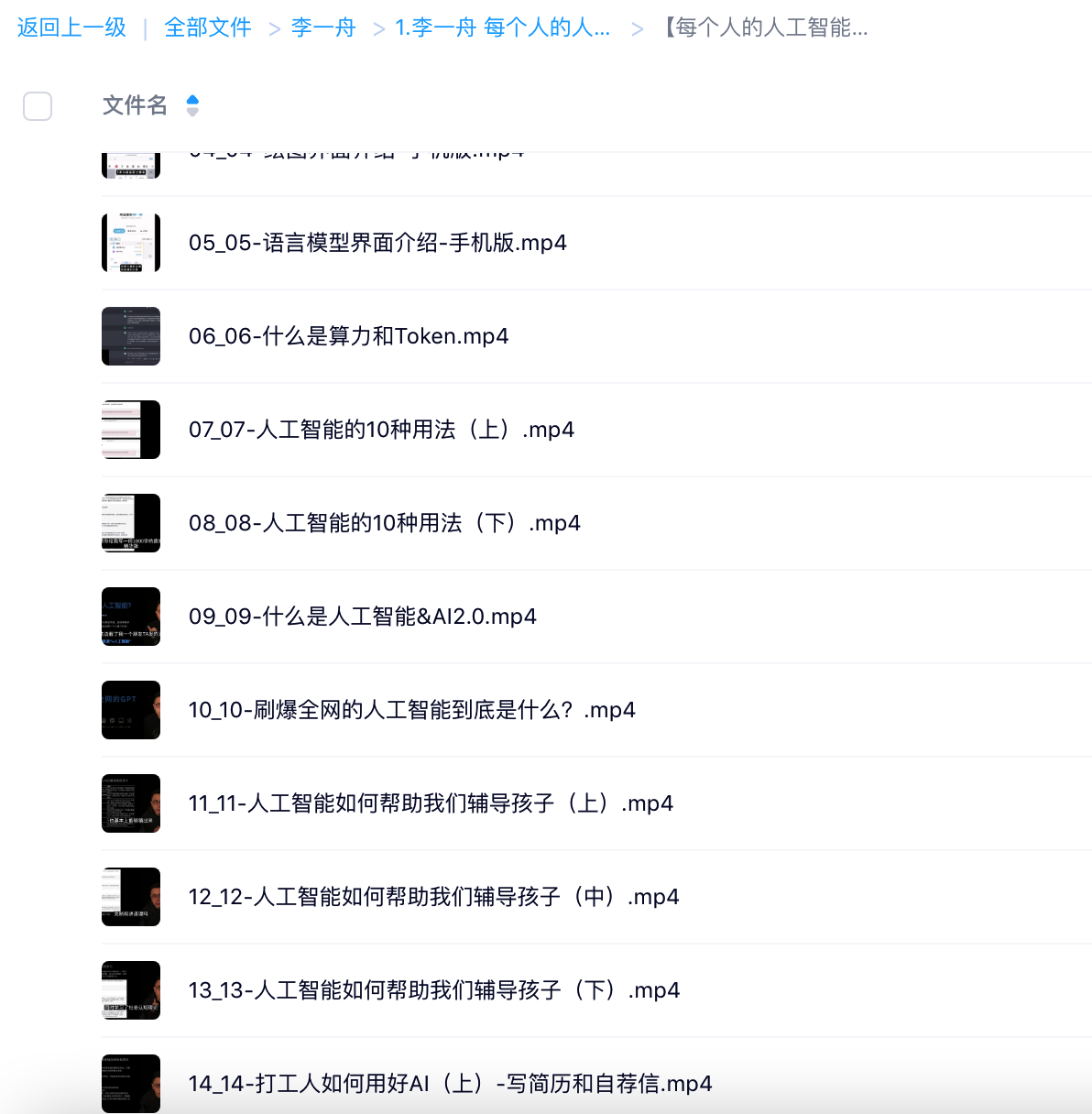
两个字符串的删除操作

dp[i][j] 表示使得[0, i-1]的word1子串和[0, j-1]的word2子串相同所需要的最小步数。
递推公式：也是分为word1[i-1]和word2[j-1]相不相等两种情况。如果相等则不需要修改，dp[i][j] = dp[i - 1][j - 1]。如果不相等，要么删除word1[i-1]，要么删除word2[j-1]，则dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1。（两个都删除的情况已经包含在其中了）
初始化按照dp数组含义即可。

class Solution {
public:
	int minDistance(string word1, string word2) {
		vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
		for(int i = 0; i <= word1.size(); i++)  dp[i][0] = i;
		for(int j = 1; j <= word2.size(); j++)  dp[0][j] = j;
		for(int i = 1; i <= word1.size(); i++) {
			for(int j = 1; j <= word2.size(); j++) {
				if(word1[i - 1] == word2[j - 1]) {
					dp[i][j] = dp[i - 1][j - 1];
				}
				else {
					dp[i][j] = min(dp[i - 1][j], dp[i][j - 1]) + 1;
				}
			}
		}
		return dp[word1.size()][word2.size()];
	}
};

编辑距离

dp[i][j] 仍然表示将[0, i-1]的word1子串转换成[0, j-1]的word2子串所需要的最少操作次数。
递推公式：在递推过程中有如下情况

if(word1[i - 1] == word2[j - 1]) {
	当前不必操作，操作次数取决于将word1[0,i-2]子串转换成word2[0,j-2]子串所需要的操作次数
}
else {
	删除，操作次数=将word1[0,i-2]子串转换成word2[0,j-1]子串所需要的操作次数+1
	或替换，将word1[0,i-2]子串转换成word2[0,j-2]子串所需要的操作次数+1
	或插入，这块有点绕弯，*word2删除一个字符，相当于word1插入一个字符*，所以插入时操作次数等于
	将word1[0,i-1]子串转换成word2[0,j-2]子串所需要的操作次数+1
}

初始化也是根据dp数组含义来就行。

class Solution {
public:
	int minDistance(string word1, string word2) {
		vector<vector<int>> dp(word1.size() + 1, vector<int>(word2.size() + 1, 0));
		for(int i = 0; i <= word1.size(); i++)  dp[i][0] = i;
		for(int j = 1; j <= word2.size(); j++)  dp[0][j] = j;
		for(int i = 1; i <= word1.size(); i++) {
			for(int j = 1; j <= word2.size(); j++) {
				if(word1[i - 1] == word2[j - 1]) {
					dp[i][j] = dp[i - 1][j - 1];
				}
				else {
					dp[i][j] = min(dp[i - 1][j - 1], min(dp[i - 1][j], dp[i][j - 1])) + 1;
				}
			}
		}
		return dp[word1.size()][word2.size()];
	}
};