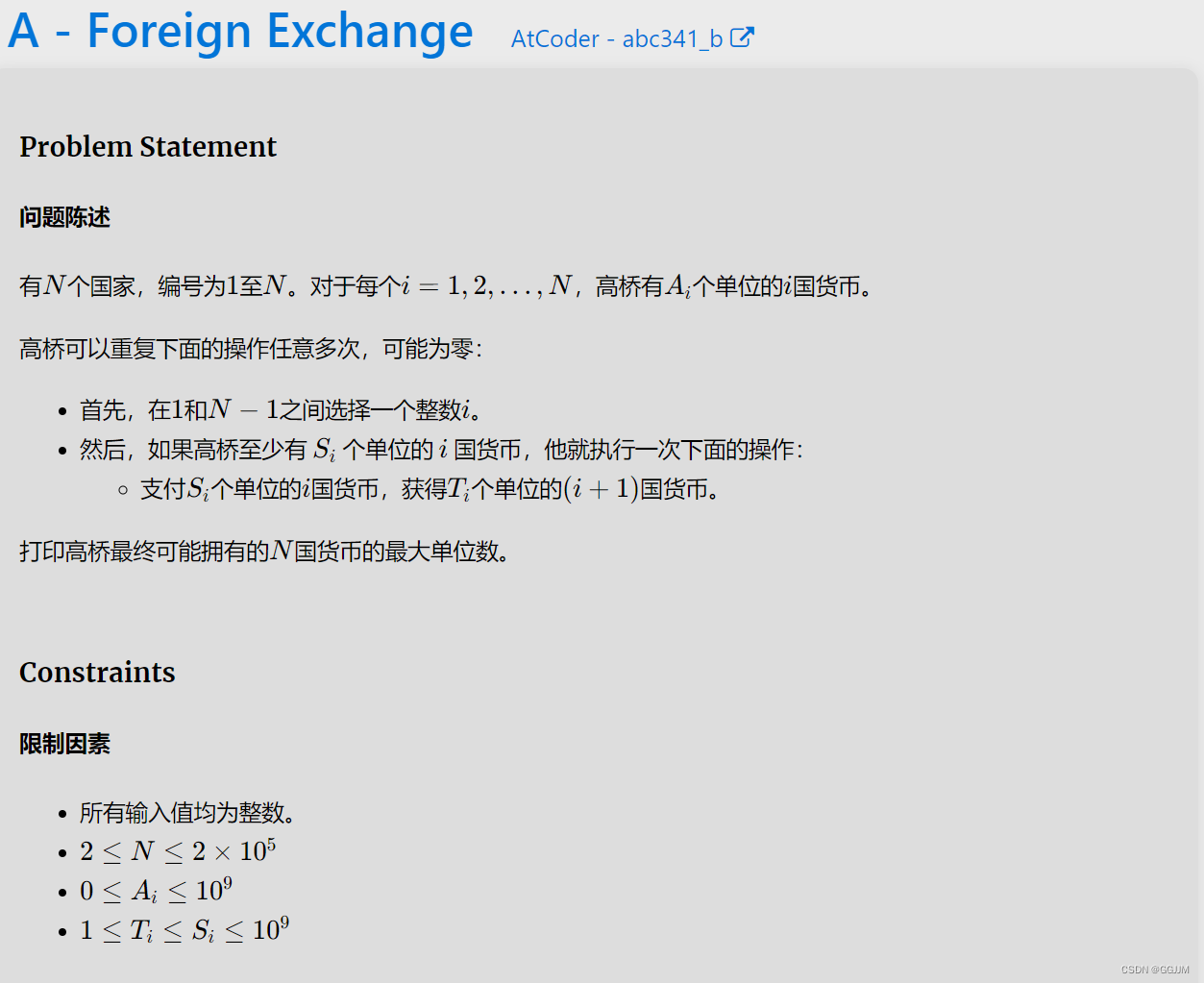
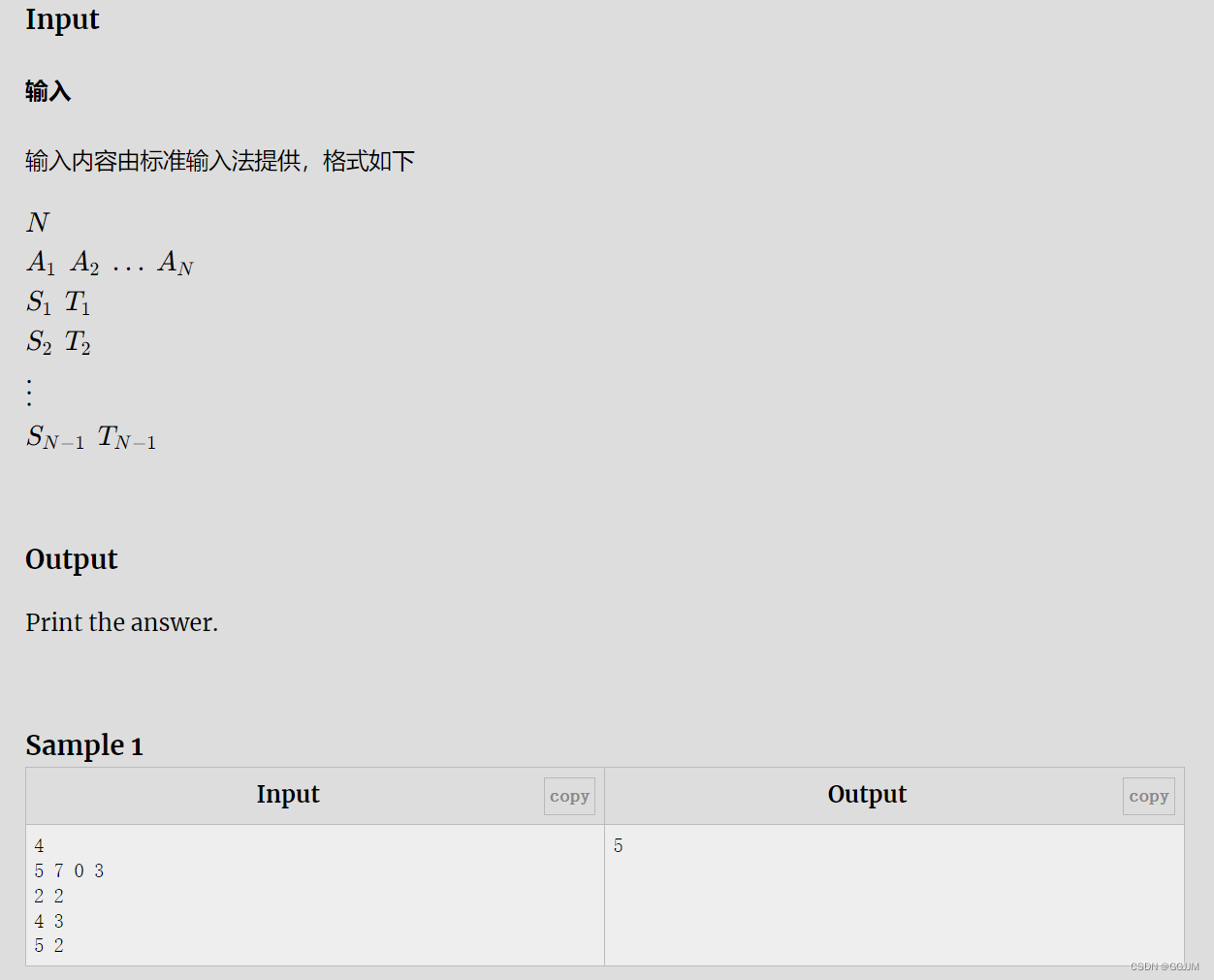
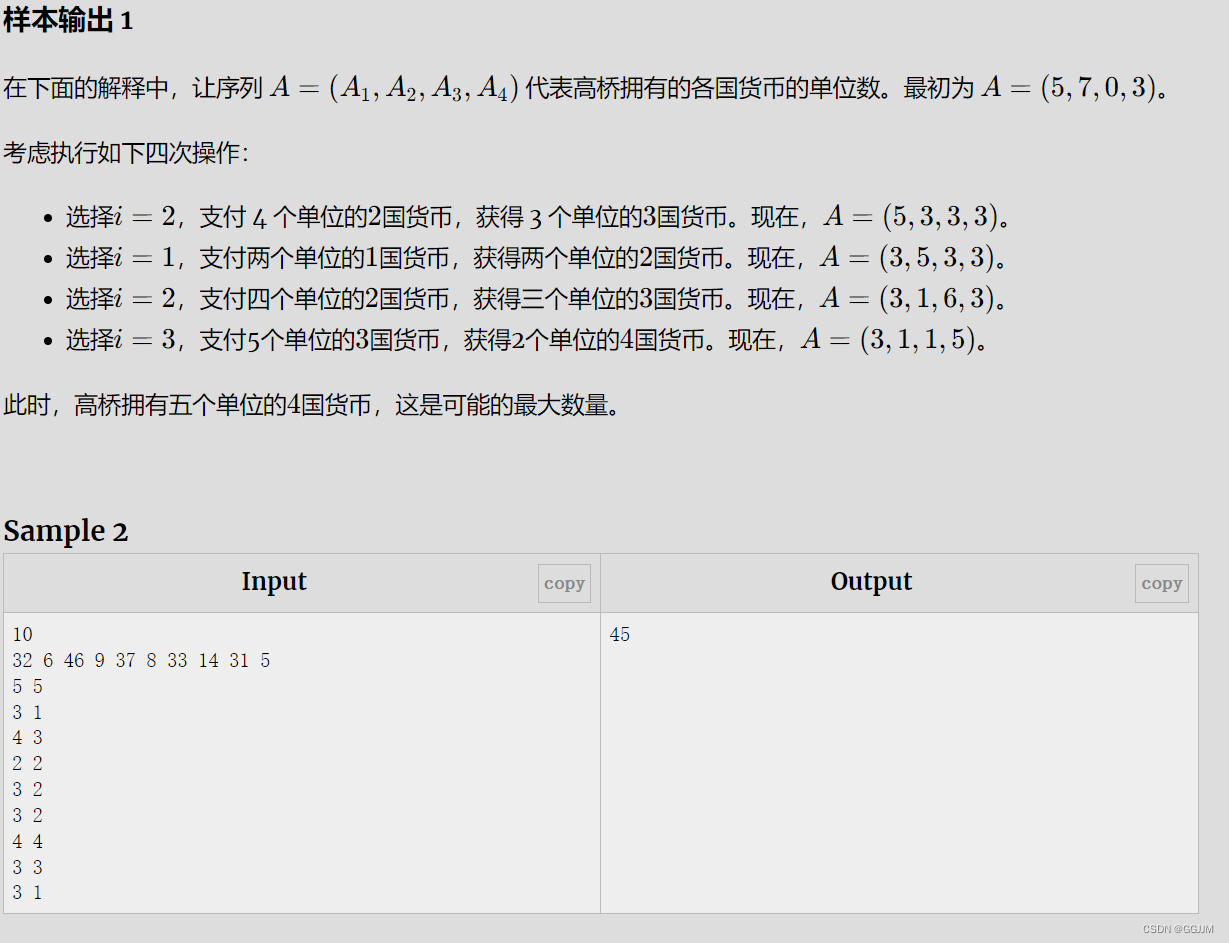
解题思路

简单模拟。

代码

#include <bits/stdc++.h>
using namespace std;
long long g[2000000];
long long n;
int main()
{
    long long x,y,z,sum=0,k=0;
    scanf("%lld",&n);
    for(x=1;x<=n;x++)
        scanf("%lld",&g[x]);
    for(x=1;x<n;x++)
    {
        scanf("%lld%lld",&y,&z);
        k=g[x]/y;
        g[x+1]+=z*k;
    }
    printf("%lld",g[x]);
    return 0;
}

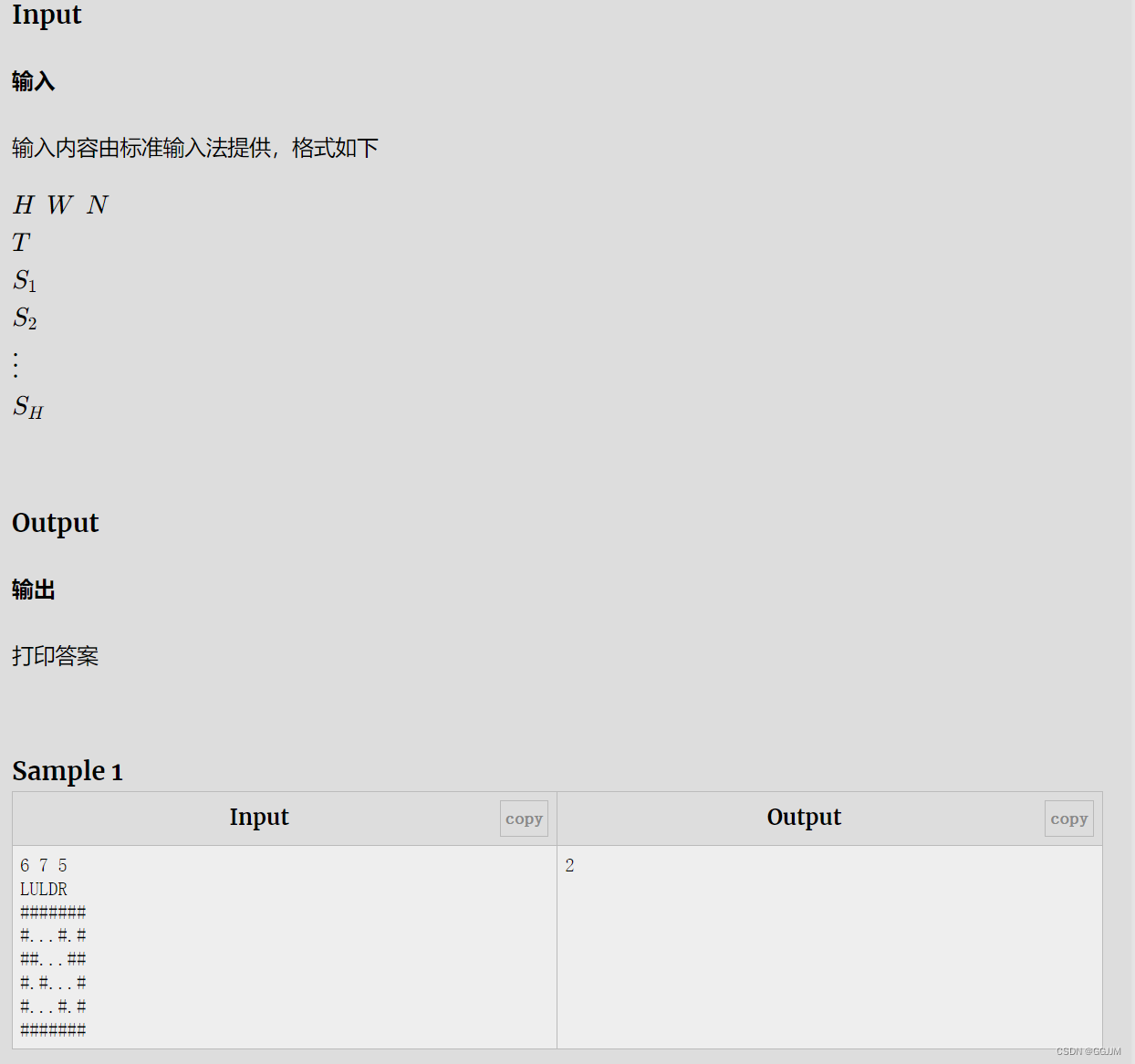
解题思路

运用dfs的方法，但搜索方向和顺序都是固定的。

代码

#include <bits/stdc++.h>
using namespace std;
char g[510][510];
int h,w,n;
char t[510];
int m[510];
int ne[5][2]={{0,0},{1,0},{0,1},{-1,0},{0,-1}};
int main()
{
    int x,y,z,l,r,tx,ty,sum=0;
    scanf("%d%d%d",&h,&w,&n);
    scanf("%s",t);
    for(x=0;t[x]!='\0';x++)
    {
        switch(t[x])
        {
            case 'L':m[x]=4;break;
            case 'U':m[x]=3;break;
            case 'R':m[x]=2;break;
            case 'D':m[x]=1;break;
        }

    }
    for(x=1;x<=h;x++)
    {
        getchar();
        scanf("%s",g[x]+1);
    }
    for(x=1;x<=h;x++)
    {
        for(y=1;y<=w;y++)
        {
            if(g[x][y]=='.')
            {
                l=x;r=y;
                for(z=0;z<n;z++)
                {
                    tx=l+ne[m[z]][0];
                    ty=r+ne[m[z]][1];
                    if(g[tx][ty]!='.')
                        break;

                    l=tx;
                    r=ty;
                }
                if(z==n)
                    sum++;
            }
        }
    }
    printf("%d",sum);
    return 0;
}

解题思路

排序一下然后模拟就行了。

代码

#include <bits/stdc++.h>
using namespace std;
long long g[110];
int main()
{
    long long t,n,sum=0;
    long long x,y,z;
    scanf("%d",&t);
    for(x=0;x<t;x++)
    {
        sum=0;
        scanf("%lld",&z);
        for(y=1;y<=z;y++)
            scanf("%lld",&g[y]);
        sort(g+1,g+z+1);
        for(y=1;y<z;y++)
            sum+=g[y+1]-g[y];
        printf("%lld\n",sum);
    }
    return 0;
}

解题思路

运用并查集来模拟连接各个村子，然后检查有几个城镇没有链接就将它链接就行了（要小心多棵树出现的情况）。

代码

#include <bits/stdc++.h>
using namespace std;
int j[1010];
struct ss
{
    int x;
    int y;
}g[1010*1010];
int find1(int x)
{
    if(j[x]==x)
        return x;
    return j[x]=find1(j[x]);
}
void unit(int x,int y)
{
    j[find1(y)]=find1(x);
}
void sset(int b)
{
    for(int x=1;x<=b;x++)
        j[x]=x;
}
int main()
{
    int n,m;
    int x,y,z,sum;
    while(1)
    {
        scanf("%d",&n);
        if(n==0)
            break;
        sset(n);
        sum=0;
        scanf("%d",&m);
        for(x=0;x<m;x++)
        {
            scanf("%d%d",&g[x].x,&g[x].y);
            if(find1(g[x].x)!=find1(g[x].y))
            {
                unit(g[x].x,g[x].y);
            }
        }
        for(x=2;x<=n;x++)
        {
            if(find1(1)!=find1(x))
            {
                unit(1,x);
                sum++;
            }
        }
        printf("%d\n",sum);
    }
    return 0;
}

# [蓝桥杯 2013 省 B] 翻硬币

## 题目背景

小明正在玩一个“翻硬币”的游戏。

## 题目描述

桌上放着排成一排的若干硬币。我们用 `*` 表示正面，用 `o` 表示反面（是小写字母，不是零），比如可能情形是 `**oo***oooo`，如果同时翻转左边的两个硬币，则变为 `oooo***oooo`。现在小明的问题是：如果已知了初始状态和要达到的目标状态，每次只能同时翻转相邻的两个硬币，那么对特定的局面，最少要翻动多少次呢？

## 输入格式

两行等长字符串，分别表示初始状态和要达到的目标状态，每行长度小于 1000。

数据保证一定存在至少一种方案可以从初始状态和要达到的目标状态。

## 输出格式

一个整数，表示最小操作步数。

## 样例 #1

### 样例输入 #1

```
**********
o****o****
```

### 样例输出 #1

```
5
```

## 样例 #2

### 样例输入 #2

```
*o**o***o***
*o***o**o***
```

### 样例输出 #2

```
1
```

代码

#include <bits/stdc++.h>
using namespace std;
char g[1010];
char j[1010];
int main()
{
    int x,y,z=0;
    scanf("%s%s",g,j);
    for(x=0;g[x]!='\0';x++)
    {
        if(g[x]!=j[x])
        {
            g[x]=j[x];
            if(g[x+1]=='*')
                g[x+1]='o';
            else
                g[x+1]='*';
            z++;
        }
    }
    printf("%d",z);
    return 0;
}