本专栏内容为：算法学习专栏，分为优选算法专栏，贪心算法专栏，动态规划专栏以及递归，搜索与回溯算法专栏四部分。 通过本专栏的深入学习，你可以了解并掌握算法。

💓博主csdn个人主页：小小unicorn
⏩专栏分类：动态规划专栏
🚚代码仓库：小小unicorn的代码仓库🚚
🌹🌹🌹关注我带你学习编程知识

题目来源

本题来源为：

Leetcode 740. 删除并获得点数

题目描述

给你一个整数数组 nums ，你可以对它进行一些操作。

每次操作中，选择任意一个 nums[i] ，删除它并获得 nums[i] 的点数。之后，你必须删除 所有 等于 nums[i] - 1 和 nums[i] + 1 的元素。

开始你拥有 0 个点数。返回你能通过这些操作获得的最大点数。

题目解析

还是老样子，先做一下预处理：
我们将数组中的数保存在arr中，转化成一次“打家劫舍”问题

算法原理

1.状态表示

经验+题目要求

对于本题而言就是：
f[i]表示：选择到i位置时，nums[i]必选，此时能获得最大点数
g[i]表示：选择到i位置时，不选nums[i]，此时能获得最大点数

2.状态转移方程

和之前一样：
在i位置选和不选两种情况

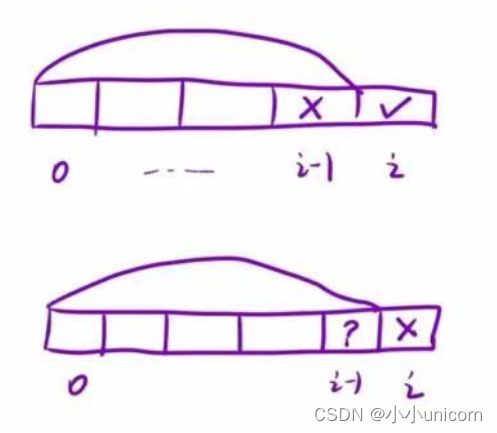
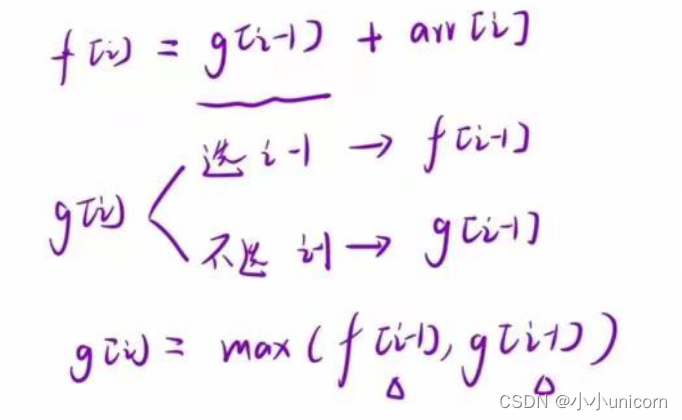
因此状态方程为：

f[i]=g[i-1]+nums[i];
g[i]=max(f[i-1],g[i-1]);

3.初始化

只有0位置会发生越界，初始化一下0位置即可

4.填表顺序

从左往右，两个表同时填

5.返回值

max(f[n-1],g[n-1])

代码实现

动态规划的代码基本就是固定的四步：

1.创建dp表
2.初始化
3.填表
4.返回值

本题完整代码实现：

class Solution 
{
public:
    int deleteAndEarn(vector<int>& nums) 
    {
        const int N =10001;
        //预处理:
        int arr[N]={0};
        for(auto x:nums)
            arr[x]+=x;
        //创建dp表
        vector<int> f(N);
        vector<int> g(N);
        //初始化
        f[0]=arr[0];
        //填表
        for(int i=1;i<N;i++)
        {
            f[i]=g[i-1]+arr[i];
            g[i]=max(f[i-1],g[i-1]);
        }
        //返回值
        return max(f[N-1],g[N-1]);
    }
};