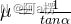CSP-J 2023 T3 一元二次方程

news2024/10/6 1:39:30

文章目录

  • 题目
    • 题目背景
    • 题目描述
    • 输入格式
    • 输出格式
    • 样例 #1
      • 样例输入 #1
      • 样例输出 #1
    • 提示
  • 题目传送门
  • 题解
    • 思路
    • 总代码
  • 提交结果
  • 尾声

题目

题目背景

众所周知，对一元二次方程 a x 2 + b x + c = 0 , ( a ≠ 0 ) ax ^ 2 + bx + c = 0, (a \neq 0) ax2+bx+c=0,(a=0)，可以用以下方式求实数解：

  • 计算 Δ = b 2 − 4 a c \Delta = b ^ 2 - 4ac Δ=b2−4ac，则:
    1. 若 Δ < 0 \Delta < 0 Δ<0，则该一元二次方程无实数解。
    2. 否则 Δ ≥ 0 \Delta \geq 0 Δ≥0，此时该一元二次方程有两个实数解 x 1 , 2 = − b ± Δ 2 a x _ {1, 2} = \frac{-b \pm \sqrt \Delta}{2a} x1,2​=2a−b±Δ ​​。

例如：

  • x 2 + x + 1 = 0 x ^ 2 + x + 1 = 0 x2+x+1=0 无实数解，因为 Δ = 1 2 − 4 × 1 × 1 = − 3 < 0 \Delta = 1 ^ 2 - 4 \times 1 \times 1 = -3 < 0 Δ=12−4×1×1=−3<0。
  • x 2 − 2 x + 1 = 0 x ^ 2 - 2x + 1 = 0 x2−2x+1=0 有两相等实数解 x 1 , 2 = 1 x _ {1, 2} = 1 x1,2​=1。
  • x 2 − 3 x + 2 = 0 x ^ 2 - 3x + 2 = 0 x2−3x+2=0 有两互异实数解 x 1 = 1 , x 2 = 2 x _ 1 = 1, x _ 2 = 2 x1​=1,x2​=2。

在题面描述中 a a a 和 b b b 的最大公因数使用 gcd ⁡ ( a , b ) \gcd(a, b) gcd(a,b) 表示。例如 12 12 12 和 18 18 18 的最大公因数是 6 6 6，即 gcd ⁡ ( 12 , 18 ) = 6 \gcd(12, 18) = 6 gcd(12,18)=6。

题目描述

现在给定一个一元二次方程的系数 a , b , c a, b, c a,b,c，其中 a , b , c a, b, c a,b,c 均为整数且 a ≠ 0 a \neq 0 a=0。你需要判断一元二次方程 a x 2 + b x + c = 0 a x ^ 2 + bx + c = 0 ax2+bx+c=0 是否有实数解，并按要求的格式输出。

在本题中输出有理数 v v v 时须遵循以下规则：

  • 由有理数的定义，存在唯一的两个整数 p p p 和 q q q，满足 q > 0 q > 0 q>0， gcd ⁡ ( p , q ) = 1 \gcd(p, q) = 1 gcd(p,q)=1 且 v = p q v = \frac pq v=qp​。

  • 若 q = 1 q = 1 q=1，则输出 {p}，否则输出 {p}/{q}，其中 {n} 代表整数 n n n 的值；

  • 例如：

    • 当 v = − 0.5 v = -0.5 v=−0.5 时， p p p 和 q q q 的值分别为 − 1 -1 −1 和 2 2 2，则应输出 -1/2；
    • 当 v = 0 v = 0 v=0 时， p p p 和 q q q 的值分别为 0 0 0 和 1 1 1，则应输出 0。

对于方程的求解，分两种情况讨论：

  1. 若 Δ = b 2 − 4 a c < 0 \Delta = b ^ 2 - 4ac < 0 Δ=b2−4ac<0，则表明方程无实数解，此时你应当输出 NO；

  2. 否则 Δ ≥ 0 \Delta \geq 0 Δ≥0，此时方程有两解（可能相等），记其中较大者为 x x x，则：

    1. 若 x x x 为有理数，则按有理数的格式输出 x x x。

    2. 否则根据上文公式， x x x 可以被唯一表示为 x = q 1 + q 2 r x = q _ 1 + q _ 2 \sqrt r x=q1​+q2​r ​ 的形式，其中：

      • q 1 , q 2 q _ 1, q _ 2 q1​,q2​ 为有理数，且 q 2 > 0 q _ 2 > 0 q2​>0；
      • r r r 为正整数且 r > 1 r > 1 r>1，且不存在正整数 d > 1 d > 1 d>1 使 d 2 ∣ r d ^ 2 \mid r d2∣r（即 r r r 不应是 d 2 d ^ 2 d2 的倍数）；

    此时：

    1. 若 q 1 ≠ 0 q _ 1 \neq 0 q1​=0，则按有理数的格式输出 q 1 q _ 1 q1​，并再输出一个加号 +；
    2. 否则跳过这一步输出；

    随后：

    1. 若 q 2 = 1 q _ 2 = 1 q2​=1，则输出 sqrt({r})；
    2. 否则若 q 2 q _ 2 q2​ 为整数，则输出 {q2}*sqrt({r})；
    3. 否则若 q 3 = 1 q 2 q _ 3 = \frac 1{q _ 2} q3​=q2​1​ 为整数，则输出 sqrt({r})/{q3}；
    4. 否则可以证明存在唯一整数 c , d c, d c,d 满足 c , d > 1 , gcd ⁡ ( c , d ) = 1 c, d > 1, \gcd(c, d) = 1 c,d>1,gcd(c,d)=1 且 q 2 = c d q _ 2 = \frac cd q2​=dc​，此时输出 {c}*sqrt({r})/{d}；

    上述表示中 {n} 代表整数 {n} 的值，详见样例。

    如果方程有实数解，则按要求的格式输出两个实数解中的较大者。否则若方程没有实数解，则输出 NO。

输入格式

输入的第一行包含两个正整数 T , M T, M T,M，分别表示方程数和系数的绝对值上限。

接下来 T T T 行，每行包含三个整数 a , b , c a, b, c a,b,c。

输出格式

输出 T T T 行，每行包含一个字符串，表示对应询问的答案，格式如题面所述。

每行输出的字符串中间不应包含任何空格。

样例 #1

样例输入 #1

9 1000
1 -1 0
-1 -1 -1
1 -2 1
1 5 4
4 4 1
1 0 -432
1 -3 1
2 -4 1
1 7 1

样例输出 #1

1
NO
1
-1
-1/2
12*sqrt(3)
3/2+sqrt(5)/2
1+sqrt(2)/2
-7/2+3*sqrt(5)/2

提示

【样例 #2】

见附件中的 uqe/uqe2.in 与 uqe/uqe2.ans。

【数据范围】

对于所有数据有： 1 ≤ T ≤ 5000 1 \leq T \leq 5000 1≤T≤5000， 1 ≤ M ≤ 1 0 3 1 \leq M \leq 10 ^ 3 1≤M≤103， ∣ a ∣ , ∣ b ∣ , ∣ c ∣ ≤ M |a|,|b|,|c| \leq M ∣a∣,∣b∣,∣c∣≤M， a ≠ 0 a \neq 0 a=0。

测试点编号 M ≤ M \leq M≤特殊性质 A特殊性质 B特殊性质 C
1 1 1 1 1 1是是是
2 2 2 20 20 20否否否
3 3 3 1 0 3 10 ^ 3 103是否是
4 4 4 1 0 3 10 ^ 3 103是否否
5 5 5 1 0 3 10 ^ 3 103否是是
6 6 6 1 0 3 10 ^ 3 103否是否
7 , 8 7, 8 7,8 1 0 3 10 ^ 3 103否否是
9 , 10 9, 10 9,10 1 0 3 10 ^ 3 103否否否

其中：

  • 特殊性质 A：保证 b = 0 b = 0 b=0；
  • 特殊性质 B：保证 c = 0 c = 0 c=0；
  • 特殊性质 C：如果方程有解，那么方程的两个解都是整数。

题目传送门

洛谷 P9750 [CSP-J 2023] 一元二次方程

题解

思路

没有任何算法，纯粹的大模拟，细节还蛮多的

由于这道题有多测，所以用一个函数比较好，可以把 a , b , c a,b,c a,b,c 都传进去，这就是主函数

int T, m;
int a, b, c;
int main() {
	scanf("%d%d", &T, &m);
	
	while(T-- && scanf("%d%d%d", &a, &b, &c))
		work(a, b, c);
	
	return 0;
}

函数里面首先是判断无解，也就是 Δ < 0 \Delta<0 Δ<0，那我们就需要算出 Δ \Delta Δ，即 b 2 − 4 a c b^2-4ac b2−4ac

int delta = b * b - 4 * a * c;

void work(int a, int b, int c) {
	delta = b * b - 4 * a * c;
	
	if(delta < 0) {
		puts("NO");
		return;
	}
}

然后需要判断 Δ \Delta Δ 是完全平方数，那么就可以直接算出 − b + Δ 2 a \frac{-b+\sqrt\Delta}{2a} 2a−b+Δ ​​ 和 − b − Δ 2 a \frac{-b-\sqrt\Delta}{2a} 2a−b−Δ ​​ 哪个大，然后如果能除开就直接输出那个根，否则就输出约分后的那个根

（那个 p r i n t d i v i s i o n ( p , q ) printdivision(p,q) printdivision(p,q) 函数是用来输出 p / q p/q p/q 的，具体请参考注释）

int delta;
double x1, x2;
int sq;

void print_division(int p, int q) {
	if(!p) {											// 分子为 0，则输出 0 
		putchar('0');
		return;
	}
	
	if(p * q < 0)										// 两数异号，则输出符号 
		putchar('-');
	
	if(p < 0)											// 将两数都变成正数 
		p = -p;
	
	if(q < 0)
		q = -q;
	
	int g = __gcd(p, q);								// 约分 
	
	p /= g;
	q /= g;
	
	if(q == 1)											// 分母为 1，则输出分子 
		printf("%d", p);
	else												// 否则输出 “分子/分母” 
		printf("%d/%d", p, q);
}

void work(int a, int b, int c) {
	delta = b * b - 4 * a * c;
	
	if(delta < 0) {
		puts("NO");
		return;
	}
	
	sq = sqrt(delta);
	
	if(sq * sq == delta) {
		x1 = 1.0 * (-b + sq) / 2 * a;
		x2 = 1.0 * (-b - sq) / 2 * a;
		
		if(x1 > x2)
			print_division(-b + sq, 2 * a);
		else
			print_division(-b - sq, 2 * a);
		
		puts("");
		
		return;
	}
}

否则的话就需要按照 “ − b / 2 a + Δ / 2 a -b/2a+\sqrt\Delta/2a −b/2a+Δ ​/2a” 的格式输出

首先如果 b ≠ 0 b\neq0 b=0，那么就说明 − b / 2 a ≠ 0 -b/2a\neq0 −b/2a=0，就可以输出 “ − b / 2 a + -b/2a+ −b/2a+”

为什么一定是 + + + ？因为如果是 − b − Δ 2 a \frac{-b-\sqrt\Delta}{2a} 2a−b−Δ ​​ 更大，那就说明 2 a < 0 2a<0 2a<0，否则不可能 − b − Δ 2 a > − b − Δ 2 a \frac{-b-\sqrt\Delta}{2a}>\frac{-b-\sqrt\Delta}{2a} 2a−b−Δ ​​>2a−b−Δ ​​，所以一定是 + + +

最后就是输出 Δ / 2 a \sqrt\Delta/2a Δ ​/2a 了，具体怎么做请参考代码注释

int delta;
double x1, x2;
int sq;

void print_division(int p, int q) {
	if(!p) {											// 分子为 0，则输出 0 
		putchar('0');
		return;
	}
	
	if(p * q < 0)										// 两数异号，则输出符号 
		putchar('-');
	
	if(p < 0)											// 将两数都变成正数 
		p = -p;
	
	if(q < 0)
		q = -q;
	
	int g = __gcd(p, q);								// 约分 
	
	p /= g;
	q /= g;
	
	if(q == 1)											// 分母为 1，则输出分子 
		printf("%d", p);
	else												// 否则输出 “分子/分母” 
		printf("%d/%d", p, q);
}

void print_sqrt(int p, int q) {
	if(q < 0)											// 如果分母是负数，则将其变为正数，因为和前面的负号消没了（上文说过了） 
		q = -q;
	
	int u = 1;											// 根号前面的系数 
	
	for(int i = sqrt(p); i > 1; --i)					// 化简 
		if(!(p % (i * i))) {
			p /= i * i;
			u *= i;
			break; 
		}
	
	int g = __gcd(u, q);								// 约分 
	
	u /= g;
	q /= g;
	
	if(u > 1)											// 系数大于 1，则输出 “系数*” 
		printf("%d*", u);
	
	if(p > 1)											// 根号下的数大于 1，则输出 “sqrt(根号下的数)” 
		printf("sqrt(%d)", p);
	
	if(q > 1)											// 分母大于 1，则输出 “/分母” 
		printf("/%d", q);
}

void work(int a, int b, int c) {
	delta = b * b - 4 * a * c;
	
	if(delta < 0) {
		puts("NO");
		return;
	}
	
	sq = sqrt(delta);
	
	if(sq * sq == delta) {
		x1 = 1.0 * (-b + sq) / 2 * a;
		x2 = 1.0 * (-b - sq) / 2 * a;
		
		if(x1 > x2)
			print_division(-b + sq, 2 * a);
		else
			print_division(-b - sq, 2 * a);
		
		puts("");
		
		return;
	}
	
	if(b) {
		print_division(-b, 2 * a);
		putchar('+');
	}
	
	print_sqrt(delta, 2 * a);
	
	puts("");
}

总代码

#include <cstdio>
#include <algorithm>
#include <cmath>
using namespace std;

int T, m;
int a, b, c;
int delta;
double x1, x2;
int sq;

void print_division(int p, int q) {
	if(!p) {
		putchar('0');
		return;
	}
	
	if(p * q < 0)
		putchar('-');
	
	if(p < 0)
		p = -p;
	
	if(q < 0)
		q = -q;
	
	int g = __gcd(p, q);
	
	p /= g;
	q /= g;
	
	if(q == 1)
		printf("%d", p);
	else
		printf("%d/%d", p, q);
}

void print_sqrt(int p, int q) {
	if(q < 0)
		q = -q;
	
	int u = 1;
	
	for(int i = sqrt(p); i > 1; --i)
		if(!(p % (i * i))) {
			p /= i * i;
			u *= i;
			break; 
		}
	
	int g = __gcd(u, q);
	
	u /= g;
	q /= g;
	
	if(u > 1)
		printf("%d*", u);
	
	if(p > 1)
		printf("sqrt(%d)", p);
	
	if(q > 1)
		printf("/%d", q);
}

void work(int a, int b, int c) {
	delta = b * b - 4 * a * c;
	
	if(delta < 0) {
		puts("NO");
		return;
	}
	
	sq = sqrt(delta);
	
	if(sq * sq == delta) {
		x1 = 1.0 * (-b + sq) / 2 * a;
		x2 = 1.0 * (-b - sq) / 2 * a;
		
		if(x1 > x2)
			print_division(-b + sq, 2 * a);
		else
			print_division(-b - sq, 2 * a);
		
		puts("");
		
		return;
	}
	
	if(b) {
		print_division(-b, 2 * a);
		putchar('+');
	}
	
	print_sqrt(delta, 2 * a);
	
	puts("");
}

int main() {
	scanf("%d%d", &T, &m);
	
	while(T-- && scanf("%d%d%d", &a, &b, &c))
		work(a, b, c);
	
	return 0;
}

提交结果

戳这里看我的提交记录
提交结果

尾声

如果这篇题解对您（或您的团队）有帮助的话，就帮忙点个赞，加个关注！

最后，祝您（或您的团队）在 OI 的路上一路顺风！！！

┬┴┬┴┤・ω・)ノ Bye~

本文来自互联网用户投稿，该文观点仅代表作者本人，不代表本站立场。本站仅提供信息存储空间服务，不拥有所有权，不承担相关法律责任。如若转载，请注明出处：http://www.coloradmin.cn/o/1463376.html

如若内容造成侵权/违法违规/事实不符，请联系多彩编程网进行投诉反馈，一经查实，立即删除！

相关文章

关于dxf文件中，多段线凸度的计算

关于dxf文件中，多段线凸度的计算

1.前言 在前面的CAD中的dxf文件解析(二)中讲到了一些CAD的dxf文件解析点、线、圆弧、圆、块等的思路。下面提供链接&#xff1a; &#xff08;二): CAD中的dxf文件解析(二):dxflib的使用_不爱学习 未完待续的博客-CSDN博客_dxflib (一)&#xff1a;CAD中的dxf文件解析(一):准备…
阅读更多...
2024.2.22 C++QT 作业

2024.2.22 C++QT 作业

思维导图 练习题 1>完善对话框&#xff0c;点击登录对话框&#xff0c;如果账号和密码匹配&#xff0c;则弹出信息对话框&#xff0c;给出提示”登录成功“&#xff0c;提供一个Ok按钮&#xff0c;用户点击Ok后&#xff0c;关闭登录界面&#xff0c;跳转到其他界面。如果账…
阅读更多...
如何将 .NET Aspire 应用程序部署到 Azure Container App

如何将 .NET Aspire 应用程序部署到 Azure Container App

作者&#xff1a;Jiachen Jiang 排版&#xff1a;Alan Wang 最近发布的用于构建云原生应用程序的 .NET Aspire 与 Azure Container App&#xff08;ACA&#xff09;非常匹配。.NET Aspire 旨在轻松管理由一系列相互依赖的微服务组成的应用程序。Azure Container App 专为微服务…
阅读更多...
Linux-时间接口-005

Linux-时间接口-005

学习重点&#xff1a; 1.函数接口 2.【ls-l】命令的实现1【time】 1.1函数原型 【time_t time(time_t *tloc);】1.2函数功能 返回1970-1-1到现在的秒数&#xff08;格林威治时间&#xff09;1.3函数参数 1.3.1【tloc】 存放秒数空间首地址 存放的秒数&#xff1a;如果【t…
阅读更多...
MySQL 窗口函数温故知新

MySQL 窗口函数温故知新

本文用于复习数据库窗口函数&#xff0c;希望能够温故知新&#xff0c;也希望读到这篇文章的有所收获。 本文以&#xff1a;MySQL为例 参考文档&#xff1a; https://www.begtut.com/mysql/mysql-window-functions.html 使用的样例数据&#xff1a;https://www.begtut.com/m…
阅读更多...
提高效率、降低成本：外贸企业必备好用ERP软件盘点

提高效率、降低成本：外贸企业必备好用ERP软件盘点

好用的外贸ERP软件有哪些&#xff1f;本期为您盘点的外贸ERP软件有&#xff1a;Zoho Books&#xff0c;孚盟M8&#xff0c;富通天下&#xff0c;睿贝软件。 外贸ERP系统是什么 企业资源规划&#xff08;ERP&#xff09;系统是一种先进的管理软件&#xff0c;尤其是在外贸和国际…
阅读更多...
如何使用Docker部署开源Leanote蚂蚁笔记并发布个人博客至公网

如何使用Docker部署开源Leanote蚂蚁笔记并发布个人博客至公网

最近&#xff0c;我发现了一个超级强大的人工智能学习网站。它以通俗易懂的方式呈现复杂的概念&#xff0c;而且内容风趣幽默。我觉得它对大家可能会有所帮助&#xff0c;所以我在此分享。点击这里跳转到网站。 文章目录 1. 安装Docker2. Docker本地部署Leanote蚂蚁笔记3. 安装…
阅读更多...
通过eeprom验证FPGA实现的单字节/页读写IIC接口时序

通过eeprom验证FPGA实现的单字节/页读写IIC接口时序

1、概括 前文设计基于FPGA的IIC接口模块&#xff0c;本文将使用eeprom来验证该模块的设计。为了便于查看读写波形&#xff0c;采用两个按键来控制对eeprom数据的读写&#xff0c;当按键0按下后&#xff0c;FPGA向eeprom的前64个存储地址写入地址对应的数据&#xff0c;当按键1按…
阅读更多...
文件上传漏洞--Upload-labs--Pass20--数组绕过

文件上传漏洞--Upload-labs--Pass20--数组绕过

一、漏洞原理 漏洞来源&#xff1a;count()函数漏洞。 现自定义一个数组 arr[]&#xff0c;定义arr[0]1,arr[3]2, 此时count(arr)的值为2&#xff0c;则arr[count[arr]]即为arr[2]&#xff0c;但是arr[2]未定义&#xff0c;即为一个空值&#xff0c;若使用count()函数的本意是…
阅读更多...
大数据计算技术秘史（上篇）

大数据计算技术秘史（上篇）

在之前的文章《2024 年&#xff0c;一个大数据从业者决定……》《存储技术背后的那些事儿》中&#xff0c;我们粗略地回顾了大数据领域的存储技术。在解决了「数据怎么存」之后&#xff0c;下一步就是解决「数据怎么用」的问题。 其实在大数据技术兴起之前&#xff0c;对于用户…
阅读更多...
【TCP/IP】组播

【TCP/IP】组播

一、组播介绍 组播&#xff08;Multicast&#xff09;是网络技术中数据传输的一种方法&#xff0c;它允许将数据包同时发送给一组指定的目标&#xff0c;而不是单个的目标&#xff08;单播 Unicast&#xff09;或所有可能的目标&#xff08;广播 Broadcast&#xff09;。组播传…
阅读更多...
Python的自定义函数

Python的自定义函数

Python的自定义函数 自定义函数的作用匿名函数语法示例 自定义函数语法示例 自定义函数的作用 定制化需求降低代码重复编写 匿名函数 匿名函数&#xff0c;可以用lambda关键字定义。通过lambda构造的函数可以没有名称&#xff0c;即在自定义匿名函数时&#xff0c;所有代码可…
阅读更多...
【智能家居】7、主程序编写+实现语音、网络和串口功能

【智能家居】7、主程序编写+实现语音、网络和串口功能

需要毕业论文私信有偿获取 截止目前mainPro.c代码 #include <stdio.h> #include <string.h>#include "controlDevices.h" #include "inputCmd.h"struct Devices *findDevicesName(char *name,struct Devices *phead){struct Devices *tmp=ph…
阅读更多...
得物面试：Kafka消息0丢失，如何实现？

得物面试：Kafka消息0丢失，如何实现？

得物面试&#xff1a;Kafka消息0丢失&#xff0c;如何实现&#xff1f; 尼恩说在前面 在40岁老架构师 尼恩的读者交流群(50)中&#xff0c;最近有小伙伴拿到了一线互联网企业如得物、阿里、滴滴、极兔、有赞、希音、百度、网易、美团的面试资格&#xff0c;遇到很多很重要的面…
阅读更多...
更改WordPress作者存档链接author和Slug插件Edit Author Slug

更改WordPress作者存档链接author和Slug插件Edit Author Slug

WordPress默认所有用户的存档永久链接都是/author/username/&#xff0c;不管是管理员还是订阅者或贡献者或作者或编辑。如果你想要自定义用户存档链接&#xff0c;比如根据角色不同使用不一样的author&#xff0c;或者自定义作者链接中的用户名Slug&#xff0c;那么建议考虑使…
阅读更多...
Win32 获取EXE/DLL文件版本信息

Win32 获取EXE/DLL文件版本信息

CFileVersion.h #pragma once#include <windows.h> #include <string> #include <tchar.h>#ifdef _UNICODE using _tstring std::wstring; #else using _tstring std::string; #endif// 版本号辅助类 class CVersionNumber { public:// 无参构造CVersionN…
阅读更多...
uniapp实现全局悬浮框

uniapp实现全局悬浮框

uniapp实现全局悬浮框(按钮,页面,图片自行设置) 可拖动 话不多说直接上干货 1,在components新建组件(省去了每个页面都要引用组件的麻烦) 2,实现代码 <template><view class"call-plate" :style"top: top px;left: left px;" touchmove&quo…
阅读更多...
探索Redis是否为单线程的奥秘（文末送书）

探索Redis是否为单线程的奥秘（文末送书）

&#x1f308;个人主页&#xff1a;聆风吟 &#x1f525;系列专栏&#xff1a;数据结构、网络奇遇记 &#x1f516;少年有梦不应止于心动&#xff0c;更要付诸行动。 文章目录 &#x1f4cb;前言一. Redis中的多线程二. I/O多线程三. Redis中的多进程四. 结论五. 书籍推荐5.1 书…
阅读更多...
OpenLayers水平镜像和垂直镜像

OpenLayers水平镜像和垂直镜像

目录 1.前言2.概念介绍2.1 旋转2.2 水平镜像2.3 垂直镜像 3.要素的镜像3.1 镜像轴始终是水平的或者垂直的3.2 镜像轴是任意角度 4.图片的镜像5.总结 1.前言 最近项目中用到了要素和图片的水平镜像和垂直镜像功能。这些功能说难不难&#xff0c;说简单也不简单&#xff0c;就是稍…
阅读更多...
【SQL注入】靶场SQLI DUMB SERIES-24通过二次注入重置用户密码

【SQL注入】靶场SQLI DUMB SERIES-24通过二次注入重置用户密码

先使用已知信息admin/admin登录进去查下题&#xff0c;发现可以修改密码 猜测可能存在的SQL语句&#xff1a;UPDATE user SET password新密码 WHERE user用户名 and password旧密码 假设我们知道有个admin用户&#xff0c;但是不知道其密码&#xff0c;如何可以将其密码重置&…
阅读更多...
推荐文章
最新文章

Copyright @ 2022~2023