题目

给定一个长度为 n 的整数数组 height 。有 n 条垂线，第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。

找出其中的两条线，使得它们与 x 轴共同构成的容器可以容纳最多的水。

返回容器可以储存的最大水量。

说明：你不能倾斜容器。

示例 1：

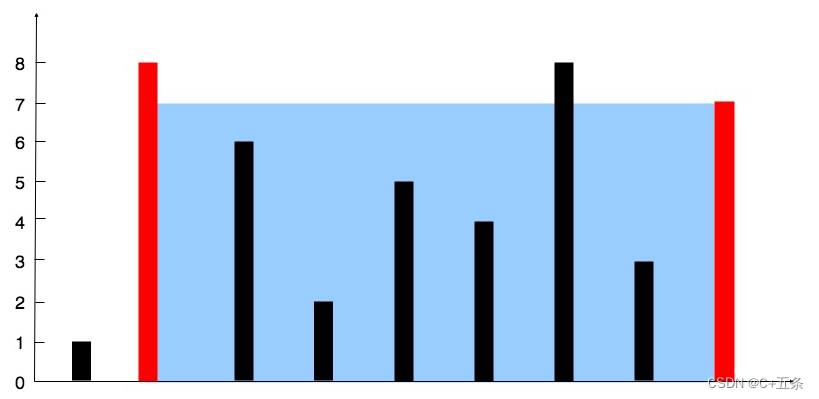
输入：[1,8,6,2,5,4,8,3,7]
输出：49 
解释：图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。在此情况下，容器能够容纳水（表示为蓝色部分）的最大值为 49。

示例 2：

输入：height = [1,1]
输出：1

 思路

题目给定一个数组让求最大容量，有以下两种方法

一、暴力枚举

从下标0开始把所有情况全部算出来求最大，及其原始暴力的方法，作为一个学习算法和编程的人，首先排除此方法。

二、双指针

此类型题目可以理解为日常生活中所说的木桶效应，一个木桶能装多少水是由最短的那块板子来决定的，同样在计算容积时，高是由最短的那个数来决定的，而想要从数组中找出最优解，枚举是不可缺少的，但要尽可能的控制枚举的次数，从而降低代码的时间复杂度。

用h表示高，w表示宽

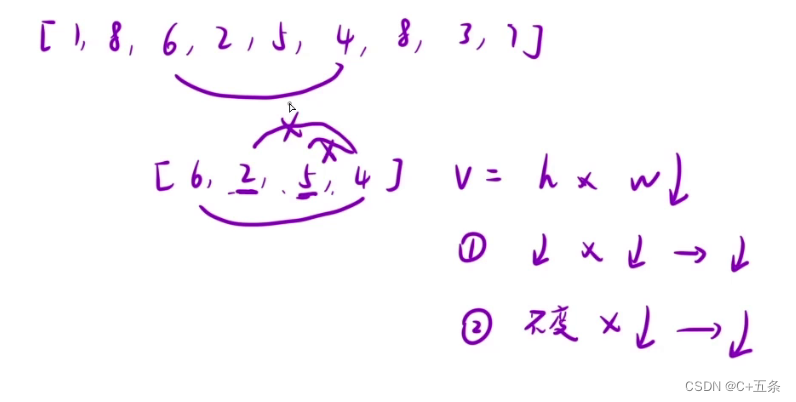
从中间随机截取一段来举例，[6,2,5,4]首先可以算出体积为3*4=12，现在假设拿4依次根其他几个数作枚举，w无疑是在减小的，那么现在会出现两种情况：

但只要仔细观察就会发现无论哪种情况，总容量都是在减少的。

1.h比4小，和刚开始比h减小了w也减小了，容量无疑也减小了。

2.h比4大，那高度还得是4，所以和刚开始比h不变，w减小，容积量在减小。

所以当在一个区间内选最左和最右两个数算出容积之后，两个数中小的那个数已经完全没有必要再去向内进行枚举了，因为无论怎么枚举，容量都是变小的。此时4可以直接不考虑了。

我们可以知道，容量是受宽和高的影响的，而我们需要找出的就是一个宽和高都相对较高的值，结合上面的分析，所以为了加快效率，两个指针一个在前一个在后同时由外向内进行遍历可以大大节约时间，那边小直接向内移动那边，然后计算容量，这样就可以用O(n)的时间复杂度来找出最大容量了。

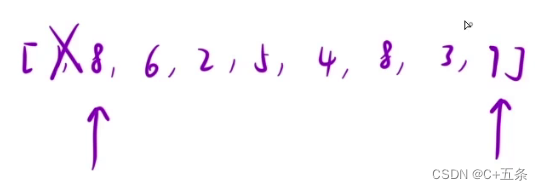
扩大到整个数组，最左最右计算完直接干掉1向右移，继续找，如果比之前算出来的都大就更新max。

题解

class Solution {
public:
    int maxArea(vector<int>& height) 
    {
        int left=0,right=height.size()-1;
        int max=0,h=0,w=0;
        while(left<right)
        {
            w=right-left;
            if(height[left]<height[right]) h=height[left++];
            else h=height[right--];
            if(w*h>max) max=w*h;
        }
        return max;
    }
};