✨个人主页: 熬夜学编程的小林
💗系列专栏: 【C语言详解】 【数据结构详解】
目录
1、整数在内存中的存储
2、大小端字节序和字节序
2.1、什么是大小端?
2.2、为什么有大小端?
2.3、练习
2.3.1、练习1
2.3.2、练习2
2.3.3、练习3
2.3.4、练习4
2.3.5、练习5
2.3.6、练习6
总结
1、整数在内存中的存储
三种表示方法均有 符号位和数值位 两部分,符号位都是用 0表示“正”,用1表示“负” ,而数值位最高位(第一位)的⼀位是被当做符号位,剩余的都是数值位。正整数的原、反、补码都相同。负整数的三种表示方法各不相同。原码:直接将数值按照正负数的形式翻译成⼆进制得到的就是原码。反码:将原码的符号位不变,其他位依次按位取反就可以得到反码。补码:反码+1就得到补码。
原因在于,使用补码,可以将符号位和数值域统⼀处理; 同时,加法和减法也可以统⼀处理(CPU只有加法器)此外,补码与原码相互转换,其运算过程是相同的,不需要额外的硬件电路。
2、大小端字节序和字节序
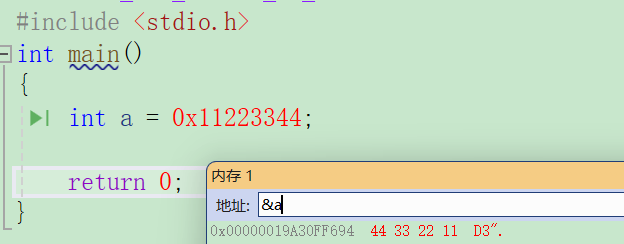
#include <stdio.h>
int main()
{
int a = 0x11223344;
return 0;
}
2.1、什么是大小端?
大端(存储)模式:是指数据的低位字节内容保存在内存的高地址处,而数据的高位字节内容,保存在内存的低地址处。小端(存储)模式:是指数据的低位字节内容保存在内存的低地址处,而数据的高位字节内容,保存在内存的高地址处。
2.2、为什么有大小端?
这是因为在计算机系统中,我们是以字节为单位的,每个地址单元都对应着⼀个字节,⼀个字节为8 bit 位,但是在C语言中除了8 bit 的 char 之外,还有16 bit 的 short 型,32 bit 的 long 型(要看具体的编译器),另外,对于位数大于8位的处理器,例如16位或者32位的处理器,由于寄存器宽度大于⼀个字节,那么必然存在着⼀个如何将多个字节安排的问题。因此就导致了大端存储模式和小端存储模式。
2.3、练习
2.3.1、练习1

//代码1
#include <stdio.h>
int check_sys()
{
int i = 1;
return (*(char *)&i);
}
int main()
{
int ret = check_sys();
if(ret == 1)
{
printf("小端\n");
}
else
{
printf("大端\n");
}
return 0;
}

思路二:
使用联合体方法,创建一个char类型和一个int类型的联合体,将int类型的数据赋值成1,如果char类型的数据也为1,则为小端。
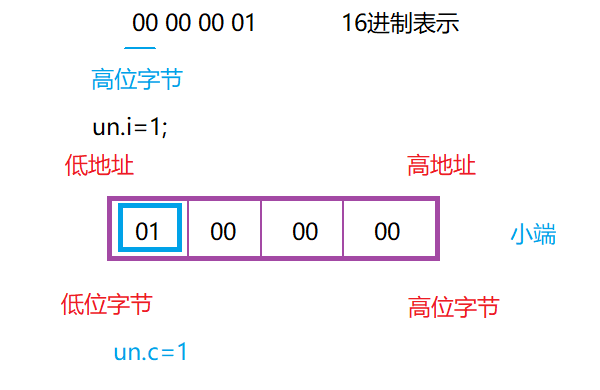
//代码2
int check_sys()
{
union
{
int i;
char c;
}un;
un.i = 1;
return un.c;
}2.3.2、练习2
#include <stdio.h>
int main()
{
char a= -1;
signed char b=-1;
unsigned char c=-1;
printf("a=%d,b=%d,c=%d",a,b,c);
return 0;
}在第十六弹的操作符(下)中我们谈到整型提升,C语言中整型算术运算总是至少以缺省整型类型的精度来进行的。( 即储存数据类型小于整型储存的32比特位时就使小于32比特位的数据类型整型提升) 为了获得这个精度,表达式中的字符和短整型操作数在使用之前被转换为普通整型(int),这种转换称为整型提升。
1. 有符号整数提升是按照变量的数据类型的符号位来提升的
2. 无符号整数提升,高位补0
我们可以知道我们一般整数进行计算时需要转化为int类型。
10000000 00000000 00000000 00000001 -1的原码
111111111 111111111 111111111 111111110 -1的反码
111111111 111111111 111111111 111111111 -1的补码
但是a的类型为char类型,因此只能存储8个bit位,即11111111 a在内存中实际存储
b的类型为signed char类型,因此只能存储8个bit位,即11111111 b在内存中实际存储
c的类型为unsigned char类型,因此只能存储8个bit位,即11111111 c在内存中实际存储
a按照%d进行打印,即10进制无符号整数打印,a为char类型,根据整型提升规则,有符号按照符号位提升,a提升之后为11111111 11111111 11111111 11111111
11111111 11111111 11111111 11111111 补码
11111111 11111111 11111111 11111110 反码
1000000 0000000 0000000 00000001 原码 值为-1 因此a打印的值为-1,b同理
c按照%d进行打印,即10进制无符号整数打印,c为unsigned char类型,根据整型提升规则,无符号在前面补0,c提升后为00000000 00000000 00000000 11111111 ----为正数,因为正数的原反补码相同,因此c的10进制值为255

2.3.3、练习3
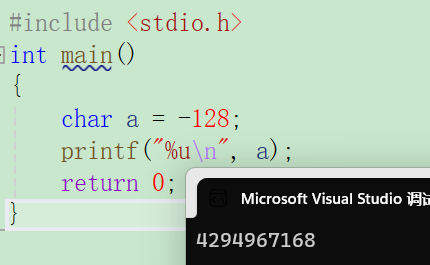
#include <stdio.h>
int main()
{
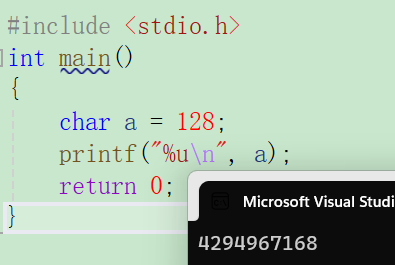
char a = -128;
printf("%u\n",a);
return 0;
}10000000 00000000 00000000 10000000 -128原码
111111111 111111111 111111111 011111111 -128反码
111111111 111111111 111111111 10000000 -128补码
a为char类型,因此a在内存中实际存储为 10000000
a按照%u进行打印,即10进制无符号打印,a首先进行整型提升,无符号按照符号位进行提升,即
11111111 11111111 11111111 10000000 提升之后
按照无符号打印,即直接打印,转化为10进制后结果为:4,294,967,168
#include <stdio.h>
int main()
{
char a = 128;
printf("%u\n",a);
return 0;
}00000000 00000000 00000000 10000000 128原、反、补码 正数都相等
a为char类型,在内存中存储为10000000
a按照%u打印,先整型提升,char类型按照符号位提升,即
11111111 11111111 11111111 10000000
10进制无符号打印即为4,294,967,168
2.3.4、练习4
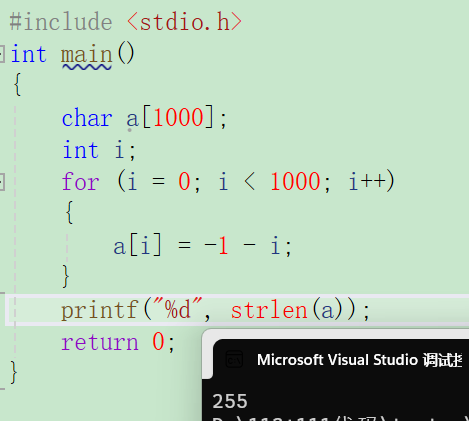
#include <stdio.h>
int main()
{
char a[1000];
int i;
for(i=0; i<1000; i++)
{
a[i] = -1-i;
}
printf("%d",strlen(a));
return 0;
}strlen计算的是'\0'之前的字符串长度,即需知道什么时候为0,循环第一次a[i]=-1-0=-1,然后-2,一直到-128,-128-1为127,然后一直减到0,中间个数有255个,因此长度为255.
2.3.5、练习5
#include <stdio.h>
unsigned char i = 0;
int main()
{
for(i = 0;i<=255;i++)
{
printf("hello world\n");
}
return 0;
}根据unsigned char类型大小的取值范围,范围为0-255,因此 i 一定小于等于255,所以此处为死循环,一直打印hello world
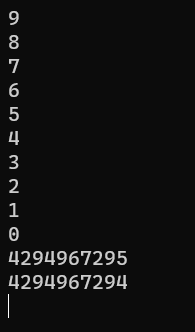
#include <stdio.h>
int main()
{
unsigned int i;
for(i = 9; i >= 0; i--)
{
printf("%u\n",i);
}
return 0;
}根据unsigned int类型大小的取值范围,范围为0-4,294,967,295,i 一定大于等于0,因此此处也为死循环,先打印9 8 7 ....0 然后打印最大值,最大值-1.....一直循环。
调试可得下图。
2.3.6、练习6
#include <stdio.h>
int main()
{
int a[4] = { 1, 2, 3, 4 };
int *ptr1 = (int *)(&a + 1);
int *ptr2 = (int *)((int)a + 1);
printf("%x,%x", ptr1[-1], *ptr2);
return 0;
}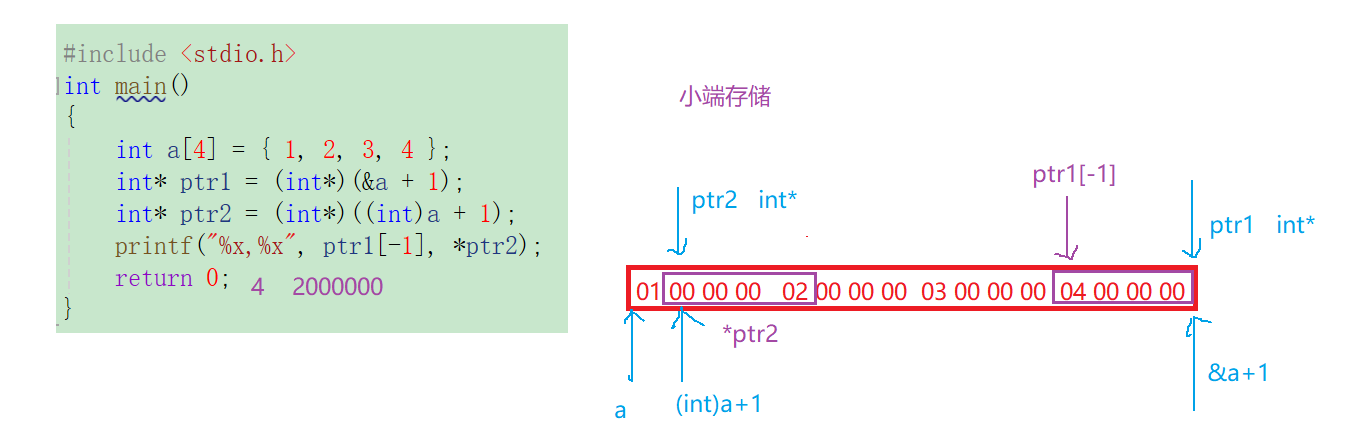
x86环境得到的结果,x64可能会出错。
总结
本篇博客就结束啦,谢谢大家的观看,如果公主少年们有好的建议可以留言喔,谢谢大家啦!