总览

dp问题的优化

要清楚：dp问题的优化一般是对dp问题的代码或者计算方程做一个等效变形
有了这个前提，我们在写dp问题时，要先将基本的代码写出来，之后再做优化

01背包问题

概述

假设我们有N个物品，我们的背包的体积是V，
N个物品每个物品有两个属性，分别是v体积、和w价值，或者说权重，每个物品要么不选，如果选的话，只能选一次
我们的目标是：要选出一些物品，在总体积能装的下的情况下（不一定必须装满），争取价值之和最大化

算法思想

Dp问题，要考虑两个问题，一个是状态表示，一个是状态计算
对于01背包问题，
状态表示：
我们先来看状态表示，因为大前提是N个物品和V的体积，也就是不算物品属性的话，我们有两个参数，所以，状态表示f，就有两个参数，那他就是二维的状态表示，f（i，j）
而对于一个状态表示 f，我们要清楚，他是一个集合，那么一个集合就会有属性，一个集合有三种属性，根据不同的题设，选择不同的属性，三种属性分别是max（元素最大值）、min（元素最小值）、数量（元素数量），本题根据题设，是属性选定为max，表示求最大价值
那这个集合的元素表示什么呢，该集合的元素表示在所有的选法中，只从前 i 个物品选择，总体积小于等于 j 的选法
总结：状态表示就是将题意数学化，将题设信息数学化为 f（i，j）
状态计算：
状态计算就是对上面的 f（i，j）进行计算，主要用到集合划分的思想
首先将集合划分为两部分，
第一个部分是 f 集合中所有不含 i 的选法的最大值，那么就是从1~i-1中选，总体积不超过 j ，也及时 f（i-1，j）
第二个部分是 f 集合中所有含 i 的选法的最大值，那么我们先将 i 排除，求得不算 i 时剩余的值最大的选法，因为排除了一个 i ，那么体积限制也跟着缩小，所以是从1~i-1中选，总体积不超过 j-vi 的选法的元素的最大值，即 f （i-1，j-vi）

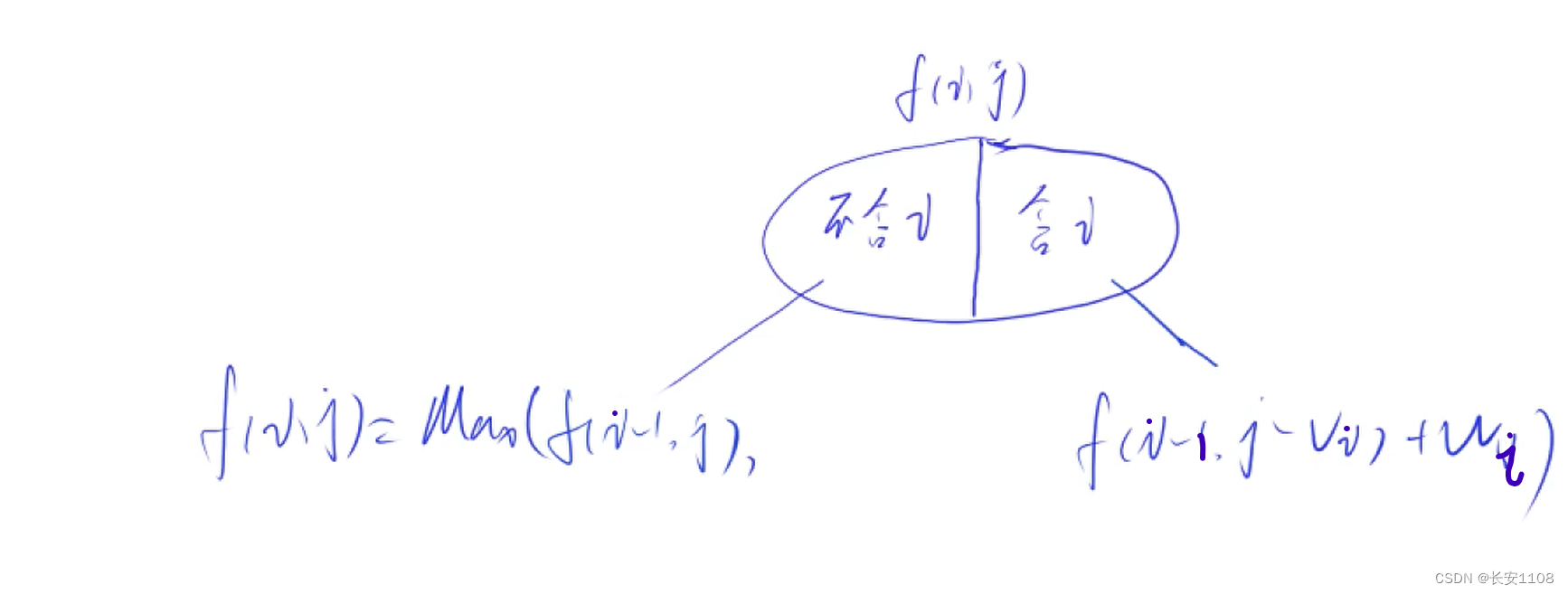
最后，将两部分取maxAPI，求得 f（i，j），注意，因为第二部分是将 i 排除之后计算得出的，所以，在取max时，第二个参数要加上i的价值wi，即第二个参数为 f（i-1，j-vi）+ wi
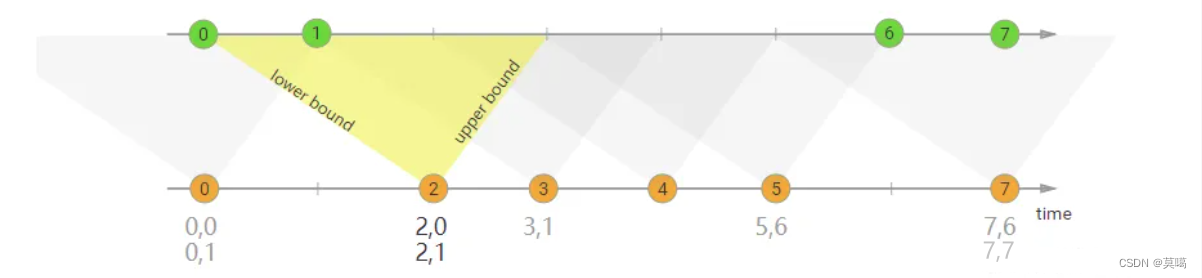
如下三张图

算法思想中的注意点

首先，f（i，j）表示在前i个物品中选，总体积不超过 j 的选法，最大价值的值
这里的i 和 j 是通量，相当于将题设扩展成普遍性了，不是题设的最终量，也就是 i 和 j在代码中是变化的，最后是要输出f（N，V）

其次，对于状态计算，不含i的部分一定会出现，含i部分未必一定会出现，所以代码中要加一个判断，代码中会体现，注意留意

例题+代码

n，m分别表示有n个物品，总体积是m
v[N],w[N]数组，分别存储每个物品的体积和价值
f[N][N]，是状态表示，也就是前i个物品中选，总体积不超过j的选法中，价值最大的值

main函数里，
首先输入n和m
然后for循环，依次向v，和w中输入值
之后，双重循环 i 从1到等于n，j从0到等于m（至于为什么i从1开始而不从0开始，是因为f[0][0~m],表示前0个物品中，选出体积不超过 j的选法，因为物品是0，所以总价值也是0，所以f[0][0到m]都是0，又因为int定义自动初始化为0，所以不用管 i =0的情况）
循环内，f[i][j] = f[i-1][j]，先将这个赋值给f[i][j]
之后判断第二部分，因为第二部分只有在 j>=v[i]时，才会出现，所以加上if判断之后，f[i][j] = max( f[i][j] , f[i-1][ j-v[i] ] + w[i] )
（因为第一步直接将值赋给了f[i][j]，所以这里是用f[i][j]进行对比，这样做的好处是，将第一部分与第二部分隔离开，因为第二部分需要特判）

完全背包问题

概述

完全背包问题，是每个物品有无限个，每个物品都可以选无限次

多重背包问题

概述

多重背包问题，是每个物品的个数不一样，也就是每个物品的可选次数不一样

分组背包问题

概述

分组背包问题，是会将物品进行分组，每一组最多只能选择改组内的一个物品，要么这个组不选，如果想选择这个组里的物品，只能选择改组内的一个物品且一次