最长回文子串------Manacher算法

目录
一、问题
二、Manacher算法基本思想
三、manacher算法对称性中的计算
四、manacher算法代码

最长回文子串------Manacher算法

一、问题

最长连续回文子序列(longest continuous palindrome subsequence，LCPS)，给定序列A，求A中按顺序连续元素构成回文的最长子序列的长度，这个子序列称为序列A的最长连续回文子序列(longest continuous palindrome subsequence)。

本题通常用来求解字符串问题，因而最长连续回文子序列也通常叫最长回文子串(longest palindromic substring，LPS)问题。

回文序列是指以序列中心位置左右对称的元素相同，也即序列以中心位置左右颠倒过来与原来是一样的。比如：'aba'、'abba'都是回文字符串。

计算机的序列是指序列的元素在代码中呈现出的顺序与内存存储顺序一致，在计算机中序列是可以通过索引来引用的。在python中字符串、列表、元组都是序列。

子序列是保持原序列中的顺序，比如：' ea ' 是' eahjkf '的子序列，但' ae '不是它的子序列。本题是关于连续回文子序列问题。比如：序列'aaaba'，它的多个连续元素构成的回文子序列为'aa'、'aaa'、'aba' 。显然，原序列本身也可以看作是自身的子序列，可以看着是特殊的子序列。

子序列可以是连续的和不连续的，这里的连续是指子序列中的元素在原序列中是不间隔、不间断的，也即在原序列中也是相邻（紧邻）的，这里的连续类似连贯的意思。本题是在一个序列中找出最长连续回文子序列(最长回文子串)的长度，考察连续性，也就是考察原序列中连续个元素的回文，找出其中最长的长度。

我们可以用动态规划算法求解最长连续回文子序列(最长回文子串)问题，下面我们利用对称性的manacher算法(manacher's algorithm)求解最长回文子串(最长连续回文子序列)问题。

Manacher算法(马拉车算法)充分利用了回文序列的对称性。回文字序列有中心对称特点，这种对称性也决定了中心左边的计算与右边的计算有关联，比如：计算到左边的值可以根据对称性得到右边的值。下面我们以字符串为例来理解manacher算法。

下面不仅求最长连续回文子序列(最长回文子串)的长度，还求出最长连续回文子序列及其个数(数量)。

二、Manacher算法基本思想

Manacher算法(马拉车算法)主要是先确定一个最长回文子串的范围，这个范围由这个回文子串的中心位置和半径就确定了，这也确定了这个回文子串的右边界位置索引right_boundary，这个中心位置center实际是for循环里的前一个i，循环到下一个i时，显然，这时的i在center的后面(即center<i)，我们找出i在center与右边界right_boundary之间的半径radius[i]，再通过while循环以步长radius[i]进行循环判断来确定radius[i]是否增加长度，radius[i]增加长度后，再判断i的右边界是否超过right_boundary，若超过，把这时的i赋给center，i的右边界赋给right_boundary，也即center，right_boundary得到了更新，然后比较最长长度与radius[i]的大小，更新最长长度，再进入for循环里的下一个i，同理上述操作，最终会求得回文子串的最长长度。

上面提到的回文子串右边界就是回文子串的最右边位置，左边界就是回文子串的最左边位置。我们可以用下面步骤更详细的表达上面的含义。下面提到i的回文子串就是以i为中心的回文子串的意思。

①确定索引0为中心的最长回文子串的范围，它的半径和右边界，0和它的回文子串右边界索引另记为center、right_boundary。

②求出i在区间(center, right_boundary)取值时的回文子串半径。在这个区间内以i为中心的回文子串半径是根据center为中心的对称性求得。i关于center对称的左侧索引记为_i，注意这里的i并不是与center只间隔1，这里i符合区间(center, right_boundary)的范围。根据回文子串的对称特点，i的回文子串半径radius[i]可以由_i的回文半径确定。

③对i的回文子串达到或越过右边界right_boundary，增长i的回文子串半径radius[i]，至此可以统计到i的完整的回文子串的半径。这一步里i的radius[i]可能经过②的计算，也可能不符合②的区间条件没有计算，在这一步才开始统计。这一步是while循环以步长radius[i]进行左右匹配判断来实现的。

④i的回文子串确定后，比较i的回文子串的右边界与right_boundary的大小，若超过right_boundary，则center的值更新为i，right_boundary的值更新为i的回文子串右边界，否则，不更新center、right_boundary。

⑤比较长度值max_length与radius[i]的大小，更新长度值max_length，然后进入i的下一个循环，重复②、③、④、⑤，最终可比较所有的回文子串长度，循环结束即可得到最终最长回文子串长度max_length。

上述算法主要思想是先确定一个回文子串(可以称为参考回文、参照回文)，根据回文子串对称性，求出下一个循环i在这个回文子串中的半径，然后以这个半径作为内循环的步长进一步确定i的回文子串的最终半径，i的回文子串半径确定后，判断i的回文子串右边界是否超过参考回文子串的右边界，若超过，则把i的回文子串作为参考回文，并比较长度值与i的回文子串半径的大小，更新长度值，并进入下一个i循环，重复上面的过程，最终获得最长回文子串长度值。

这个算法提高速度的点是充分利用已经计算的半径，借助对称性，获得后面位置的临时半径，并以这个临时半径为循环步长进一步确定这个临时半径的最终半径。这减少了循环次数。

三、manacher算法对称性中的计算

要实现manacher算法(Manacher's Algorithm)，我们先要对原字符串做增加字符的处理。字符串的元素个数有偶数和奇数，做额外增加字符处理，统一变为奇数字符串，这样任何一个字符可以作为回文子串的中心位置，比如:回文子串A='abba'的中心位置实际是没有字符，但经过下面这种处理变为'#a#b#b#a#'，它任何一个元素位置都可以作为中心。

Manacher算法在计算时主要是确定回文子串的中心和半径，还会用到回文子串的右边界，但右边界显然可以由中心和半径求得。回文子串的半径是指以中心位置向左的元素个数且包括中心位置的这个元素个数，显然，半径也是以中心位置向右的元素个数且包括中心位置的这个元素个数。中心值是某个元素的索引。

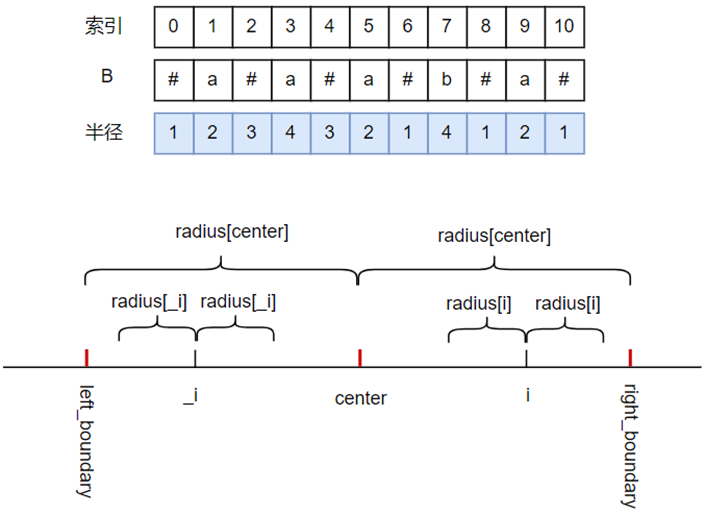
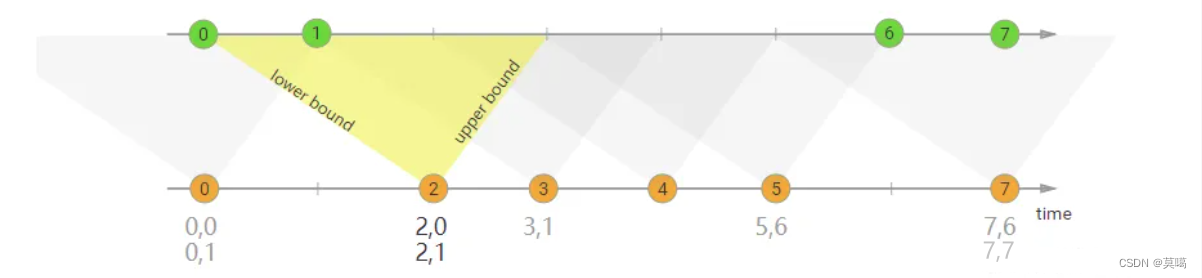
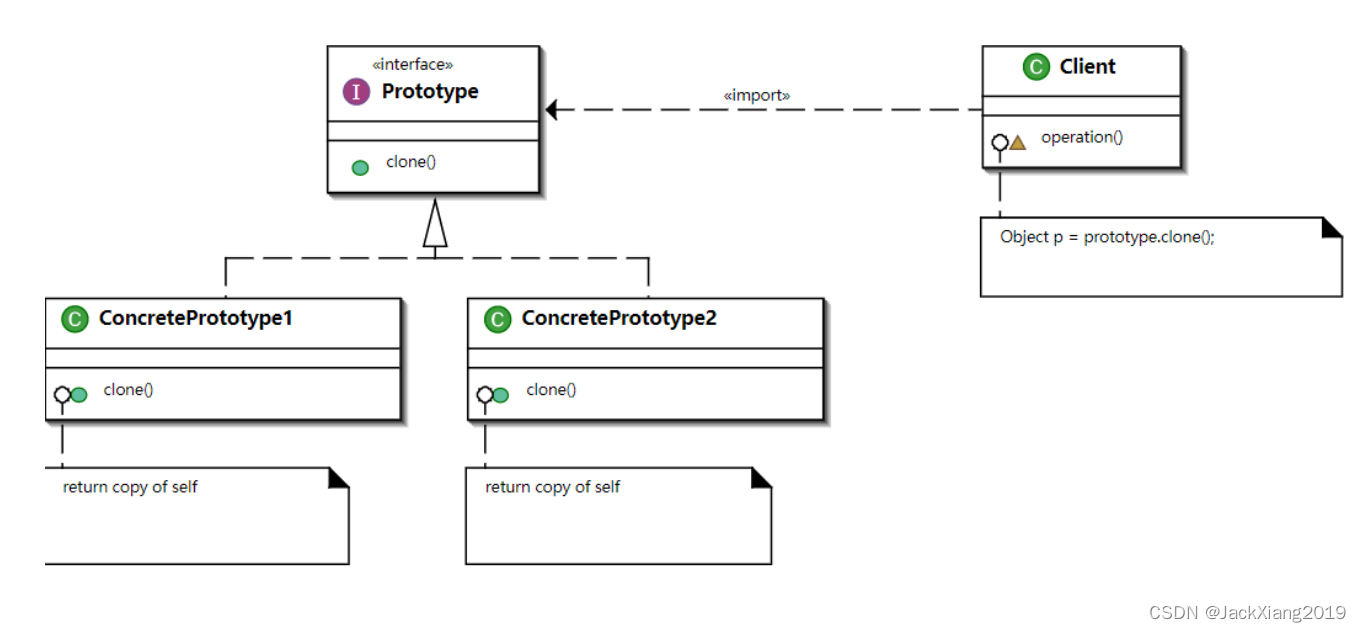
图3-1 manacher算法对称关系

图3-1中center为中心的回文子串左边界索引为left_boundary，右边界索引为right_boundary，半径记为radius[center]，显然，由center、radius[center]可以得到left_boundary、right_boundary，center的回文子串可以称为参考回文(参照回文)。

在代码计算中，center左侧的索引位置实际已经计算了，而center右侧的索引位置是有待计算的，那么根据回文子串的对称性特点，我们可以利用左侧的值来求右侧的值，也即图中_i与i是对称的，我们可以利用_i的回文子串求i的回文子串的性质。比如：若_i的回文子串半径在center的回文子串边界内，则i的回文子串半径与_i的回文子串半径是一样的，它们的回文子串也是一样的，它们是确定的，不会在增长，若_i的回文子串半径超过了left_boundary，i的回文子串真正半径至少到达了右边界right_boundary，受取值范围的影响(center< i < right_boundary)，这时候统计到的i的半径可以称为i的回文子串的临时半径，有待进一步统计，这时候i的回文子串真正半径不一定与_i的回文子串半径相等，因为已经越过center回文子串边界，超过部分不一定再以center对称。根据对称性，有_i=2 * center – i，_i到left_boundary的距离与i到right_boundary的距离是相等的，即right_boundary - i=_i-left_boundary。

四、manacher算法代码

下面Manacher算法(Manacher's Algorithm)就充分利用了这些由回文子串对称性特点决定的性质，先确定center，然后求i，获得i的回文子串若超过center的右边界，则i的回文子串作为参考回文(参照回文)，也即新的center回文子串，下一个循环的i以这个新的center回文子串作为参照计算，以此类推，就把字符串的每个位置计算了一遍。具体计算的详细过程参见下面manacher算法代码。代码的理解可以结合上面的分析、图3-1，以及代码的注释来理解。

#最长连续回文子序列(最长回文子串)长度。
def manacher(A):
    #回文序列是指以序列中心位置左右对称的元素相同,也即序列以中心位置左右颠倒过来与原来是一样的。
    #最长连续回文子序列(回文子串)是在原序列连续元素构成的回文子序列。
    #字符串的元素个数有偶数和奇数,做下面额外增加字符处理,统一变为奇数字符串,方便以一个中心及半径区域进行统计。
    #先对字符串A的两端外侧分别增加'#',字符串A的中间位置分别增加'#',A应该不含有'#',这样方便替换回来。
    #做下面处理后,任何字符串都变为奇数个,且下面字符串B的任何一个位置都可以作为中心位置。
    #若没有做下面处理,当A为偶数个字符时,比如:回文A='abba'的中心位置实际是没有字符,
    #但经过下面这种处理变为'#a#b#b#a#',它任何一个元素位置都可以作为中心。
    B = '#' + '#'.join(A) + '#'
    n = len(B)

    #radius存放各位置的半径,这里的半径也就是以中心位置向左的元素个数且包括中心位置的这个元素个数,
    #显然,半径也是以中心位置向右的元素个数且包括中心位置的这个元素个数。
    #下面初始化为0,后面代码会统计每个位置作为中心位置时回文子串的最大半径。
    radius = [0] * n

    #center对应为B的元素的索引,right_boundary是以center位置为中心的的最长回文子串的右边界的索引。
    #确定它的右边界,根据对称性,它的左边界left_boundary也能确定。
    #但因为字符串是从左到右判断回文子串,这里我们只需要用到它的右边界的值,
    #显然首个元素索引为0,且回文子串是它自身,因而右边界为0。
    #下面循环中会不断更新这两个值,它们是由i,radius[i]生成的。
    #下面提到的右边界、左边界就是以center位置为中心的right_boundary、left_boundary,
    #center、right_boundary、left_boundary是B中对应的索引号。

    #首个元素构成回文,其索引为回文子串的中心。
    center = 0
    #首个元素位置的以center=0为中心位置半径为1的最大回文子串,也就是首个元素自身。
    radius[0] = 1
    #首个元素构成的回文子串的右边界也即是center的位置。
    right_boundary = 0
    #对应到A中的回文子串长度。下面会比较更新这个值,最终会得到最大值。
    max_length = 0

    #上面0索引已经计算了,下面索引从1开始。
    for i in range(1,n):
        #下面这个条件语句主要是针对初始i=0,和在确定好以center中心后,i在center的右边界内以i为中心的半径情况,
        #找出i的半径是方便下面while中可能用到,用这个i的半径作为循环步长可以提高while循环效率。
        #并不是所有的i都会执行下面条件语句体内的语句,
        #当通过循环后i的值达到或越过了center的右边界right_boundary,则直接进入下面while循环的判断。

        #对于每个给定的center,right_boundary,下面实际是判断i在区间(center,right_boundary)取整数的情形,
        #因为center,right_boundary实际在下面由i,radius[i]决定了,除了上面0索引位置的以外。
        #center上面初始值为0,通过循环后,当i>0时,每次循环到i,i实际总是在center的后面,即center<i,
        #因为在循环到该次之前通过判断用之前的i、radius[i]确定好center,right_boundary的值,
        #循环到这次就是下一个i,因而i在center之后。
        #可见,考察i在以center为中心的最长回文子串中的情况,只需要考察i在区间(center,right_boundary)的取值。
        #对于i达到或越过right_boundary,则直接在while中判断统计。

        #当循环到i时,实际上i之前的radius[0],radius[1],...,radius[i-1]已经依据下面代码计算好了。
        #我们记i关于center中心对称的左侧位置为_i,根据对称性,则有_i=2 * center - i。

        #下面重点讨论center<i < right_boundary条件下的等式的确定。
        #i在center<i < right_boundary的范围里,i到右边界的半径为right_boundary - i,见下面代码的注释。
        #因而i在center<i < right_boundary的范围里统计到的radius[i]值应该是radius[i]≤right_boundary - i。
        #此时并不知道以i为中心的回文子串分布情况,但根据对称性,我们可以考察与i对称的_i的情况,从而得到i的情况。
        #简单地讲,我们需要考察_i,因为它已经计算了,而i是有待计算的,
        #根据回文子串对称性特点,i与_i存在联系,因而可以根据_i来确定此时i的情况。
        #根据对称性显然有right_boundary - i=_i-left_boundary。

        #对于_i,radius[_i]也有可能radius[_i]<_i-left_boundary,radius[_i]<right_boundary - i,
        #以_i为中心的回文子串在center的左边界与center范围里,
        #根据对称性可知,以i为中心的回文子串在center与center的右边界范围里,
        #实际上,这时候,根据i与_i关于center中心对称可得radius[i]=radius[_i]<right_boundary - i,
        #也就是讲,这时候,它们相等且小于right_boundary - i。
        #由于这时候回文子串在以center为中心的边界范围内,回文子串半径是已经确定的,不需要扩展,
        #因此,遇到这种情形时并不执下面while循环体内语句。

        #对于_i,radius[_i]有可能有radius[_i]≥_i-left_boundary,也即radius[_i]≥right_boundary - i,
        #因为_i在center的左侧,以_i为中心的回文子串可能达到或越过center的左边界,
        #此时,根据i与_i关于center中心对称可知,以i为中心的回文子串至少达到center的右边界,
        #只是i在center<i < right_boundary的范围里,我们最多能得到radius[i]值为right_boundary - i,
        #有可能我们还没有统计完整,也即还有待统计(下面的while会做进一步判断统计),
        #但这时候i为中心的回文子串的真正半径不一定与radius[_i]相等,因为此时越界后可能不再以center中心对称。

        #因此,综合上述两种情形,i在center<i < right_boundary的范围里,
        #统计到的radius[i]值应该为radius[_i]和right_boundary - i中的最小值。
        #但这里统计到radius[i]可能不是完整统计,是局部范围的结果,可能有待进一步统计,
        #下面while中会进行判断扩展i的半径,也即可能对radius[i]做更完整的统计。

        if center< i < right_boundary:
            #注意上面半径的定义,而center<=i < right_boundary,
            #则半径right_boundary - i=right_boundary-1- i+1,
            #前面减1因为i小于right_boundary,后面加1就是加上i这个中心位置。
            #这里的right_boundary由下面计算所得,可以参见下面代码的计算公式。
            radius[i] = min(radius[2 * center - i], right_boundary - i)

        #while对回文子串半径radius[i]的扩展(增加长度),也就是对处于或越过center的右边界时需要判断是否扩展(增加长度)。
        #因此,上面条件语句计算的radius[i],在下面不一定再计算,只有处于或越过center的右边界的才可能再次计算radius[i]。

        #尝试扩展以i为中心的半径为radius[i]的回文子串。
        #i - radius[i],i + radius[i]是在已经确定的回文子串的左右分别扩展(增加)一个字符进行比较,
        #若在字符串范围内且相等,说明以i为中心的半径radius[i]值增加1。
        #下面循环相当于在i的基础上以半径radius[i]为步长进行循环,这减少了循环次数,因此,提高了计算效率。
        while i - radius[i] >= 0 and i + radius[i] < n and B[i - radius[i]] == B[i + radius[i]]:
            radius[i] += 1

        #下面实际是对上面半径增值(扩展)后才执行条件内的更换中心和右边界,否则,不执行。
        #上面while循环若更新radius[i]值后,也即半径增值,则下面条件为真。

        #判断以i为中心在半径radius[i]下的右边界radius[i] + i - 1是否比原来right_boundary大,
        #若大,则更新center,right_boundary,也就是把这时的i,radius[i]+ i - 1分别赋给它们。
        #若不大,说明还在原中心center及右边界right_boundary范围里,
        #不需要更新,跳过下面条件判断,经过下面max比较后进入下一个循环。
        if radius[i] + i - 1 > right_boundary:
            center = i
            right_boundary = radius[i] + i - 1

        #更新最长回文子串的长度。
        #按上述增加符号后B中i位置最长回文子串长度应该为2*radius[i]-1,减去1因为重复了一个中心,
        #这个i位置最长回文子串去掉上述增加的符合,还原成A的字符,则对应的最长回文子串长度为radius[i]-1,
        #因为按上述方式增加符号,回文子串中相当于增加了radius[i]个符号,因而,去掉这些增加的符号,
        #则有radius[i]-1=2*radius[i]-1-radius[i]。
        max_length = max(max_length, radius[i]-1)

    return max_length


A = 'aaaba'

print(manacher(A))

运行结果：

在上面的while循环中以步长radius[i]进行循环降低了循环次数，从而提高了运行效率。根据上面的代码我们也可以求出所有的最长回文子串及个数(数量)。

#最长连续回文子序列(最长回文子串)长度。最长连续回文子序列(最长回文子串)及个数(数量)。
def manacher(A):

    B = '#' + '#'.join(A) + '#'
    n = len(B)

    radius = [0] * n

    center = 0
    radius[0] = 1
    right_boundary = 0
    max_length = 0

    max_sub=[]
    num=0
    #上面0索引已经计算了,下面索引从1开始。
    for i in range(1,n):
        if center< i < right_boundary:
            radius[i] = min(radius[2 * center - i], right_boundary - i)

        while i - radius[i] >= 0 and i + radius[i] < n and B[i - radius[i]] == B[i + radius[i]]:
            radius[i] += 1

        if radius[i] + i - 1 > right_boundary:
            center = i
            right_boundary = radius[i] + i - 1

        if radius[i]-1>max_length:
            num=1
            max_sub=[[B[i - radius[i]+1:i + radius[i]-1].replace('#','')]]
            max_length = radius[i]-1
        elif radius[i]-1==max_length:
            num+=1
            max_sub.append([B[i - radius[i]+1:i + radius[i]-1].replace('#','')])

    return max_length,max_sub,num


A = 'aaaba'

max_length,max_sub,num=manacher(A)
print('最长回文子串的长度:',max_length)
print('最长回文子串:',max_sub)
print('最长回文子串的个数(数量):',num)

运行结果：