目录
1、线性回归的原理
1.1 应用场景
1.2 什么是线性回归
1.2.1 定义
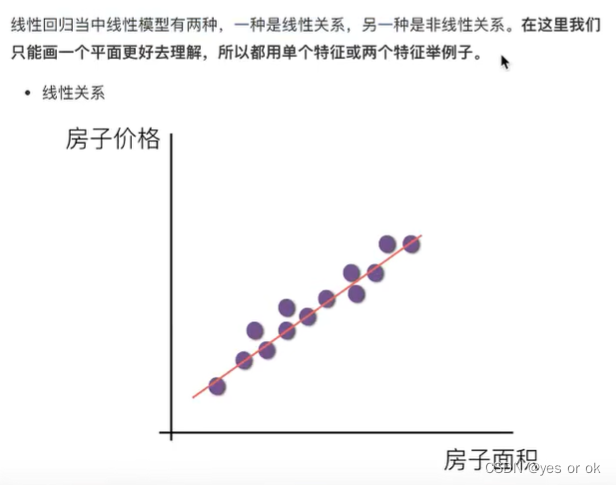
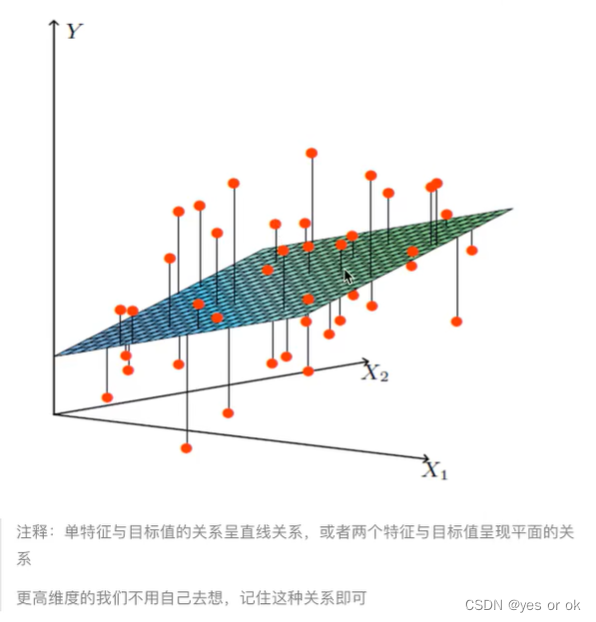
1.2.2 线性回归的特征与目标的关系分析
2、线性回归的损失和优化原理
2.1 损失函数
2.2 优化算法
2.2.1 正规方程
2.2.2 梯度下降
3、线性回归API
4、回归性能评估
5、波士顿房价预测
5.1 流程分析
5.2 代码
6、正规方程和梯度下降对比
7、梯度下降优化器
- 线性回归
- 欠拟合与过拟合
- 线性回归的改进 - 岭回归
- 分类算法:逻辑回归
- 模型保存与加载
- 无监督学习:K-means算法
1、线性回归的原理
回归问题:
目标值:连续性的数据
1.1 应用场景

1.2 什么是线性回归
1.2.1 定义

1.2.2 线性回归的特征与目标的关系分析
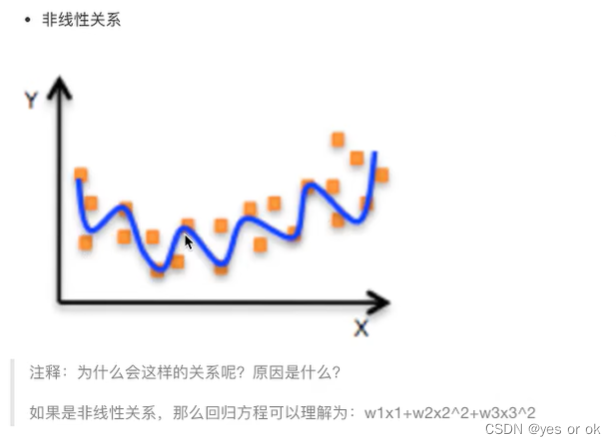

2、线性回归的损失和优化原理

2.1 损失函数

2.2 优化算法

2.2.1 正规方程

2.2.2 梯度下降

学习率:步长
3、线性回归API

4、回归性能评估

5、波士顿房价预测
5.1 流程分析
- 获取数据集
- 划分数据集
- 特征工程
- 无量纲化 - 标准化
- 预估器流程
- fit() --> 模型
- coef_ intercept_
- 模型评估
5.2 代码
from sklearn.datasets import load_boston
from sklearn.metrics import mean_squared_error
from sklearn.model_selection import train_test_split
from sklearn.preprocessing import StandardScaler
from sklearn.linear_model import LinearRegression, SGDRegressor
def linear1():
# 正规方程的优化方法对波士顿房价进行预测
# 1、获取数据
boston = load_boston()
# 2、划分数据集
x_train,x_test,y_train,y_test=train_test_split(boston.data,boston.target,random_state=22)
# 3、标准化
transfer = StandardScaler()
x_train=transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、预估器
estimator = LinearRegression()
estimator.fit(x_train,y_train)
# 5、得出模型
print("正规方程-权重系数为:\n",estimator.coef_)
print("正规方程-偏置为:\n",estimator.intercept_)
# 6、模型评估
y_predict = estimator.predict(x_test)
print("正规方程-预测房价:\n",y_predict)
errror = mean_squared_error(y_test,y_predict)
print("正规方程-均方差误差:\n",errror)
return None
def linear2():
# 梯度下降的优化方法对波士顿房价进行预测
# 1、获取数据
boston = load_boston()
# 2、划分数据集
x_train, x_test, y_train, y_test = train_test_split(boston.data, boston.target, random_state=22)
# 3、标准化
transfer = StandardScaler()
x_train = transfer.fit_transform(x_train)
x_test = transfer.transform(x_test)
# 4、预估器
estimator = SGDRegressor()
estimator.fit(x_train, y_train)
# 5、得出模型
print("梯度下降-权重系数为:\n", estimator.coef_)
print("梯度下降-偏置为:\n", estimator.intercept_)
# 6、模型评估
y_predict = estimator.predict(x_test)
print("梯度下降-预测房价:\n", y_predict)
errror = mean_squared_error(y_test, y_predict)
print("梯度下降-均方差误差:\n", errror)
return None
if __name__ == "__main__":
# 代码1 :正规方程的优化方法对波士顿房价进行预测
linear1()
# 代码2:梯度下降的优化方法对波士顿房价进行预测
linear2()6、正规方程和梯度下降对比

7、梯度下降优化器




![[bing]“gang调度 Kubernetes的并发控制和一致性机制“论点的对应的源码分析](https://img-blog.csdnimg.cn/direct/afea1bdfb04f4776945aec79e0a4abc3.png)





![NDK的log.h使用__android_log_print报错app:buildCMakeDebug[x86_64]](https://img-blog.csdnimg.cn/direct/8a09cb7fd33c4e26adbae634917d7ed8.png)