目录
二叉树基础知识
概念 :
根节点的五个形态 :
特殊的二叉树
满二叉树 :
完全二叉树 :
二叉搜索树 :
平衡二叉搜索树 :
二叉树的性质 :
二叉树的存储结构
二叉树的顺序存储结构
二叉树的链式存储结构
二叉树的遍历方式 :
基础概念
前中后遍历
层序遍历 :
二叉树基础知识
概念 :
二叉树(binary tree)是指树中节点的度不大于2的有序树,它是一种最简单且最重要的树。二叉树的递归定义为:二叉树是一棵空树,或者是一棵由一个根节点和两棵互不相交的,分别称作根的左子树和右子树组成的非空树;左子树和右子树又同样都是二叉树。
根节点的五个形态 :
-
空二叉树
-
只有一个根结点
-
根结点只有左子树
-
根结点只有右子树
-
根结点既有左子树又有右子树
特殊的二叉树
满二叉树 :
概念 :
如果一棵二叉树只有度为0的结点和度为2的结点,并且度为0的结点在同一层上,则这棵二叉树为满二叉树。
图例 :

完全二叉树 :
概念 :
在完全二叉树中,除了最底层节点可能没填满外,其余每层节点数都达到最大值,并且最下面一层的节点都集中在该层最左边的若干位置。若最底层为第 h 层(h从1开始),则该层包含 1~ 2^(h-1) 个节点。
图例 :

而

这个就不是一颗完全二叉树!
二叉搜索树 :
前面介绍的树,都没有数值的,而二叉搜索树是有数值的了,二叉搜索树是一个有序树。
- 若它的左子树不空,则左子树上所有结点的值均小于它的根结点的值;
- 若它的右子树不空,则右子树上所有结点的值均大于它的根结点的值;
- 它的左、右子树也分别为二叉排序树
下面的就是一颗二叉搜索树;

二叉搜索树最大的特点就是左<父<右 ;
平衡二叉搜索树 :
又被称为AVL(Adelson-Velsky and Landis)树,且具有以下性质:它是一棵空树或它的左右两个子树的高度差的绝对值不超过1,并且左右两个子树都是一棵平衡二叉树。
其中c++中的map、set、multimap,multiset的底层实现都是平衡二叉搜索树,所以map、set的增删操作时间时间复杂度是logn , 而unordered_map、unordered_set,unordered_map、unordered_set底层实现是哈希表。
二叉树的性质 :
-
二叉树的第i层上至多有2 ^ (i-1)(i≥1)个节点。
-
深度为h的二叉树中至多含有2^h-1个节点
-
若在任意一棵二叉树中,有 n0 个叶子节点,有 n2 个度为2的节点,则必有n0 = n2 + 1
-
具有n个节点的完全二叉树深为log2(x) + 1(其中x表示不大于n的最大整数)
-
若对一棵有n个节点的完全二叉树进行顺序编号(1<=i<=n),那么,对于编号为i(i>=1)的节点:
⑴i =1 时,该节点为根,它无双亲节点 。
⑵ i > 1 时,该节点的双亲节点的编号为i/2 。
⑶2i<= n,则有编号为2i的左节点,否则没有左节点 。
⑷2i+1<=n ,则有编号为2i+1的右节点,否则没有右节点 。
二叉树的存储结构
二叉树可以顺序存储,也可以链式存储 ;
二叉树的顺序存储结构
二叉树的顺序存储结构就是用一维数组存储二叉树中的结点,并且结点的存储位置,也就是数组的下标要能体现结点之间的逻辑关系,比如双亲与孩子的关系,左右兄弟的关系等。
如以下这颗完全二叉树 :

可以采用以下线性表来存储:
| 下标 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 | 9 | 10 |
|---|---|---|---|---|---|---|---|---|---|---|
| 数据 | A | B | C | D | E | F | G | H | I | J |
如果父节点的数组下标是 i,那么它的左孩子就是 i * 2 + 1,右孩子就是 i * 2 + 2。
二叉树的链式存储结构
在链式结构中,一个二叉树的结点包含左孩子指针,数据,右孩子指针 ;

链式存储效果如图 :
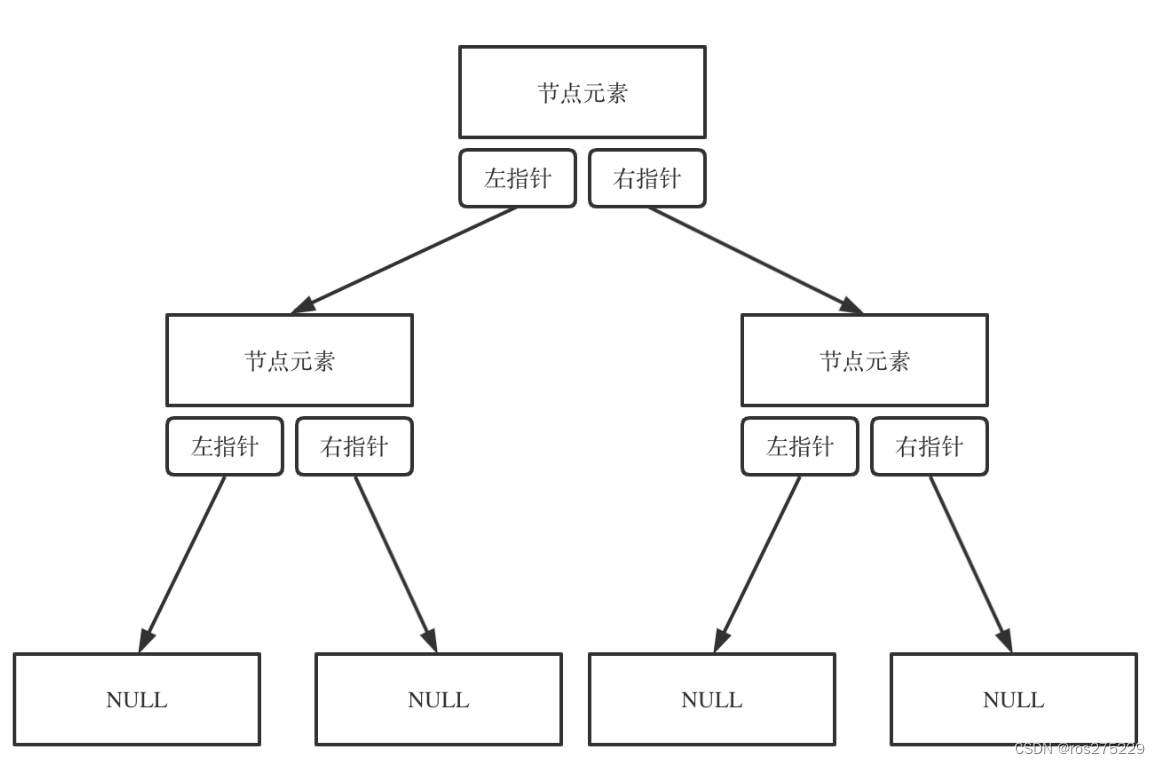
二叉链表的结构体定义 :
typedef struct BiTNode
{
TElemType data; //数据域
struct BiTNode *lchild,*rchild; //指针域
}BiTNode,*BiTree;二叉树的遍历方式 :
基础概念
首先,主要的两种遍历方式为 :
- 深度优先遍历:先往深走,遇到叶子节点再往回走。
- 广度优先遍历:一层一层的去遍历。
这两种遍历方法又可以细分 :
- 深度优先遍历
- 前序遍历(递归法,迭代法)
- 中序遍历(递归法,迭代法)
- 后序遍历(递归法,迭代法)
- 广度优先遍历
- 层次遍历(迭代法)
前中后遍历
其中前中后三种结点的遍历顺序 如下 :
- 前序遍历:中左右
- 中序遍历:左中右
- 后序遍历:左右中
图例 :

层序遍历 :
从树的第一层开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问 ;
如下图 :
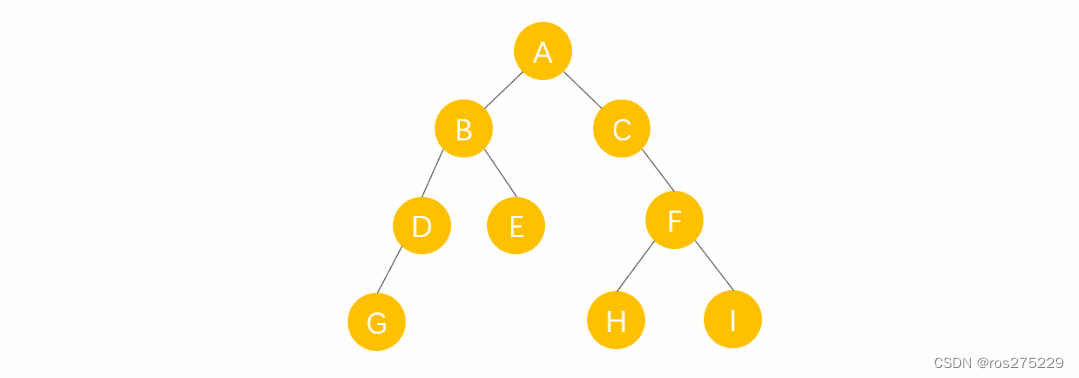
层序遍历的结果为 :
ABCDEFGHI
参考 :
-
《大话数据结构》
-
《数据结构》C语言版(清华严蔚敏考研版)
-
【数据结构与算法】二叉树
-
代码随想录