[论文阅读] 空间熵图像增强算法(Spatial Entropybased Contrast Enhancement in DCT)

最近看到了一篇介绍传统图像增强算法的文章：基于空间熵的对比度增强算法 - 知乎 (zhihu.com)，从里面看到效果还不错，如下所示，因而详细看了下。

首先在网上找到了这篇文章及代码，如下：
文章：Spatial Entropy-Based Global and Local Image Contrast Enhancement, [paper]，[code]

同时还找到了另外一篇博客来介绍这篇文章：基于空间熵的全局和局部图像对比度增强 - BrianX - 博客园 (cnblogs.com)。
这2篇博客介绍说明的差不多，说的都很详细，但个人觉得没有把这篇算法的本质说清楚，下面说说我对这个算法的理解。

1. 算法原理

算法主要可以分为2个步骤：

1. 全局直方图均衡
2. 局部对比度增强

1.1 全局直方图均衡

这篇文章中的全局直方图均衡与一般的全局直方图均衡有点不一样。

一般的全局直方图均衡是统计整幅图像的直方图来进行的，它会增强整幅图像中出现的更多的灰度，这样会使得增强后的图像出现一些问题，如对于大片平坦区域，增强后可能会出现失真，对一般全局直方图均衡可详见这里：一文搞懂直方图均衡_直方图均衡算法-CSDN博客。

那这篇文章中的算法使用什么方法来改善这些问题了？

• 一是使用分块统计来替代全局统计，改善全局出现最多像素的影响：文章中将图像均匀的分割成K=M*N块，K<=graylevel(对于8位的图像，graylevel=256)，然后对每块单独统计直方图，得到二维直方图H，H的大小是graylevel*K，每行是一个灰阶在每个块中出现的次数(概率)，每列是每块的直方图。
• 二是使用熵对比度来替代出现次数作为权重，改善出现少的像素权重：文章中将二维直方图中的每一行，也就是每个灰度，计算一个熵，得到每个灰度的熵Sk，即文中公式3，使用每个灰度的熵与其他所有灰度熵的和的比值fk，即文中公式4，来替代次数作为权重。

来看下文章中给的一个例子：

图中，a为原图，b为全局直方图均衡结果，c为使用文中方法结果。可以看到，全局直方图均衡对直方图中出现比较多的灰度增强较多，而对出现较少的灰度则有一定的抑制，使得增强后的图像存在问题，而文章中的方法则好很多。

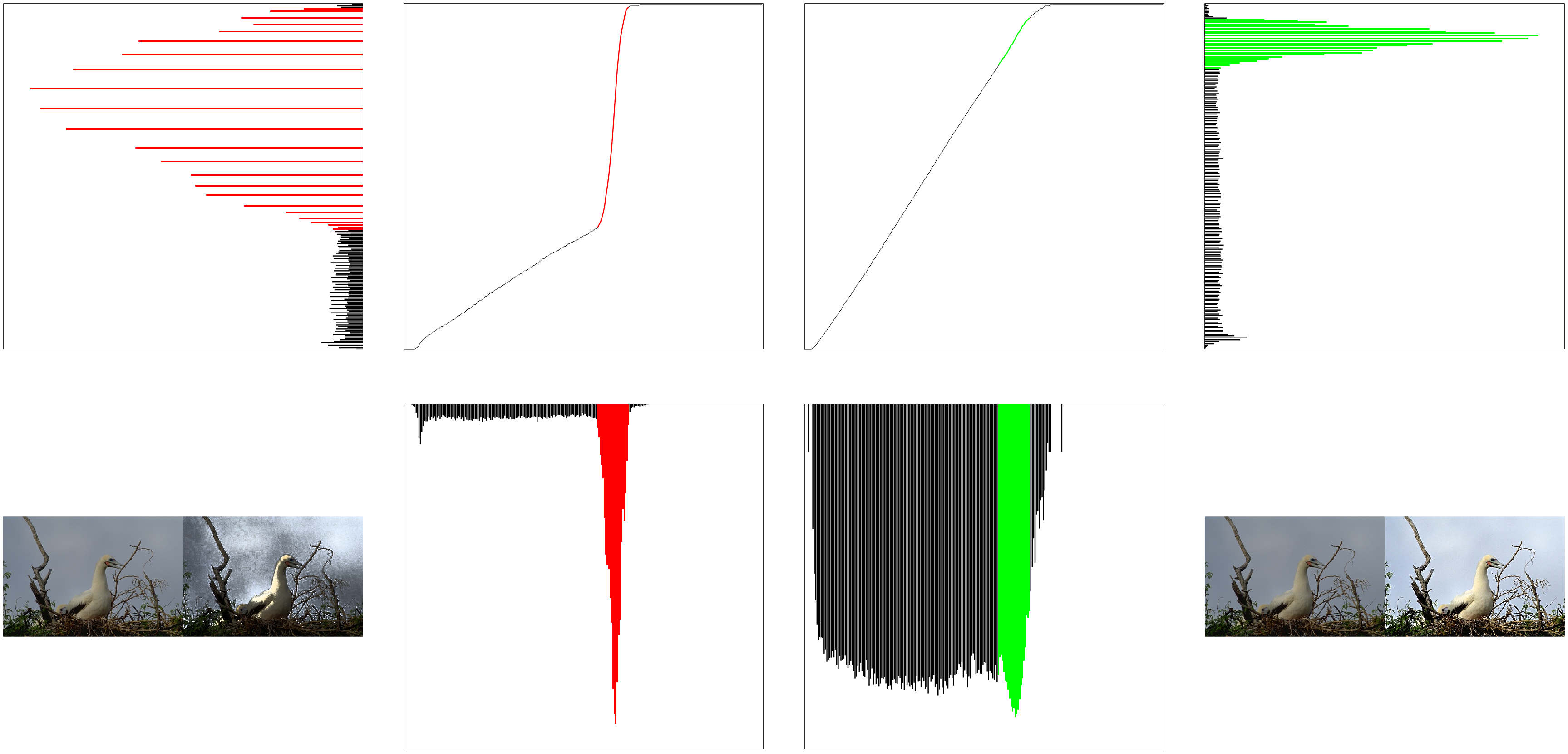
上面图像可以更直观的反映出二者区别。从左到右，从上到下，依次标号为1-8，左边4幅图像，1(增强后直方图)、2(CDF，映射曲线)、5(增强结果)、6(直方图)为全局直方图均衡结果，右边4幅图像，3(CDF，映射曲线)、4(增强后直方图)、7(熵对比度fk)、8(增强结果)为文章中结果。

可以看到，文章中方法对直方图中出现较多的灰度没有过度增强，没有出现增强太过的问题。

1.2 局部对比度增强

文章中的局部对比都增强方法比较简单，利用了DCT变换的性质，对DCT变换后的系数乘以一个大于1的数，这个数是第一步里面自适应算出来的一个数，详见文中公式12，即使用fk计算出来熵的r次幂。关于图像DCT可以查看：图像处理中的DCT变换 - 知乎 (zhihu.com)

上图为文章中的一个例子，c为文章中方法均衡后的结果，d是DCT细节增强后的结果。

2. 原理拆解

下面尝试分析下算法原理的本质。

2.1 全局直方图均衡

首先来看下文章每个灰度的熵(详细了解熵，可以戳这里：详解机器学习中的熵、条件熵、相对熵和交叉熵 - 遍地胡说 - 博客园 (cnblogs.com))。

熵可以用来表示数据的混乱程度(确定性)，概率越均匀，熵越大，概率越不均匀，熵越小。

对应于图像中的每个灰度，在每个块中出现的次数越平均，其熵Sk越大；在每个块中出现的次数越不平均，其熵Sk越小。熵Sk最大为 $-\frac{1}{K}\ast log\left(\frac{1}{K}\right)$，K为图像分成的块数，按文章中的方法，K一般在256左右，当K=256时，Sk最大为0.0313。

因而，在文章中，熵是用来表示每个灰度在图像中分布的均匀程度，分布越均匀，熵越大；分布越不均匀，熵越小。

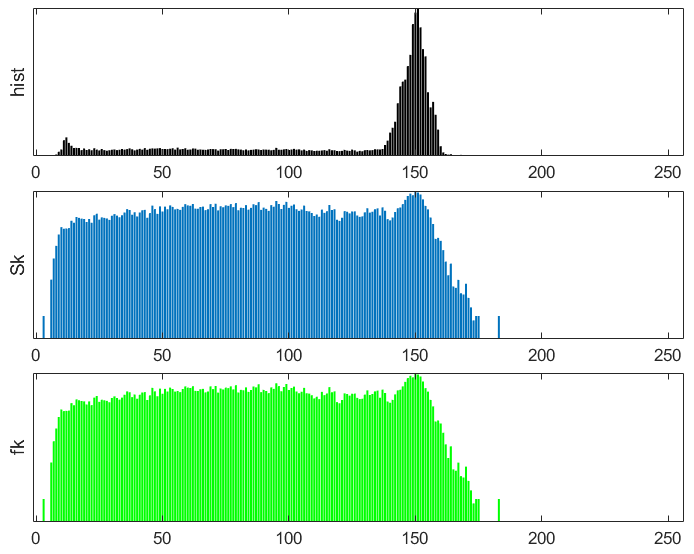
上图为示例中有鸭子(可能不是)的图像对应的直方图hist、熵Sk、及熵的对比度fk。从图中可以看到，每个灰度的熵Sk与直方图中对应的概率没有很明显的关系，可以看到，灰度的熵Sk不会因为其概率很大而很大，概率很小而很小，这样可以避免使用灰度直方图的问题。

再来看看熵对比度fk。从上图中可以看到，熵对比度fk与熵Sk几乎是一样的。看看其计算公式可能就明白了，fk=Sk/(S-Sk)，S为所有灰度熵Sk的和，S远大于Sk，相当于fk=Sk/S。

由于灰度的熵Sk变化相对较小，由其计算CDF来作为映射曲线就相对平滑，可以看到上面例子中，映射曲线差不多就是一条直线，类似于线性拉伸。

对代码中提供的图像进行了测试，发现其映射曲线基本都类似线性拉伸。整体上，文章的全局直方图均衡有类似线性拉伸的作用。

2.2 局部对比度增强

局部对比度增强就比较简单，使用DCT变换对细节增强，就不再详细说明了，主要是计算系数，下面是不同的alpha的结果。

上图中，左边alpha=1.2，右边alpha=1.8。alpha越大对细节增强越明显，如图中下方树枝。

而文章中方法，使用第一步中计算出来的fk来计算 $\alpha ={\left({\sum }_{k=1}^K\left(f_{k}lo{g}_2\left(f_k\right)\right)\right)}^{\gamma }$。由于fk分布相对比较均匀，因而计算出来的alpha可能都差不多。

统计了代码中提供的测试图像，计算出来的alpha基本都为1.6x。整体上，alpha的变化范围可能比较小。