基于 GTSAM 的因子图简单实例

Title: 基于 GTSAM 的因子图简单实例

文章目录

I. 引言
II. GTSAM 的安装与配置
III. 基于 GTSAM 的因子图实例的 C++ 实现
- 1. C++ 源码
- 2. CMakeLists.txt 脚本
- 3. 数值结果
IV. 基于 GTSAM 的因子图实例的 Python 实现
- 1. Python 源码
- 2. 数值结果
- 3. 可视化结果
V. 总结

关联博文:

因子图、边缘化与消元算法的抽丝剥茧 —— Notes for “Factor Graphs for Robot Perception”
基于 GTSAM 的因子图简单实例

I. 引言

在上一篇博文中, 围绕因子图的构建和运行原理, 分析了因子图的定义、消元与边缘化算法等.

此处基于开源库 GTSAM, 构建和应用一下因子图.

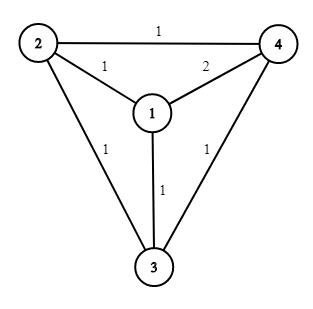
就从一个简单的实例展开 —— 上一博文中的 “一个简单的 SLAM 中的因子图例子”.

SLAM 例子:

机器人先验的初始起点为 $x_1$ , 在该点上进行了一元测量 (Unary Measurement, 如 GPS、UWB 等绝对位姿测量) $z_1$ ; 同时又探测到了路标 $l_1$ 并进行了二元测量 (Binary Measurement, 如激光扫描测量) $z_2$ .

然后机器人前进到了新的地点 $x_2$ , 并记录了从 $x_1$ 到 $x_2$ 的里程计信息; 在该点上也侦测到了路标点 $l_1$ 并进行了二元测量 $z_3$ .

机器人继续前进到 $x_3$ 并记录了这一段路程的里程计信息; 同时, 机器人在该点观察到了另一个路标点 $l_2$ 并记录了测量结果 $z_4$ .

Fig. 1 一个简单的 SLAM 中的因子图例子

II. GTSAM 的安装与配置

先安装和配置环境.

序号	处理
1	下载源码 https://github.com/borglab/gtsam, 注意 checkout 最新的稳定版本.
2	cmake-gui 查看编译参数
3	命令行运行 mkdir build cd build cmake … -DCMAKE_INSTALL_PREFIX=指定路径/gtsam_4.2 -DGTSAM_BUILD_PYTHON=ON -DGTSAM_BUILD_DOCS=ON make -j4 make install make python-install 注意: 替换"指定路径"为自己实际安装路径
4	配置环境参数
5	卸载 [不完全卸载] 编译时建立的build文件夹下, 运行命令 make uninstall [完全卸载] 编译时建立的build文件夹下, 运行命令 xargs rm -rf < install_manifest.txt

III. 基于 GTSAM 的因子图实例的 C++ 实现

1. C++ 源码

一共 9 个因子, 涉及先验因子、里程计因子、二元测量因子、自定义一元测量因子等.

难点在于自定义一元测量因子的构建.

一元测量因子用于建模 UWB、GPS等, 此处以二维平面上的起始位姿状态 $\mathbf{x}_1=(x, y, \theta)$ 为例, 对应的测量值为 $\mathbf{m}=(m_x, m_y)$ . 则位置误差/残差为
$\mathbf{r}(\mathbf{x}_1) = \begin{bmatrix} x - m_x \\ y - m_y \end{bmatrix}$
则 $\mathbf{r}$ 相对于 $\mathbf{x}_1$ 在位置测量值/测量点 $\mathbf{m}$ 上的 Jacobian 矩阵 (雅可比矩阵) 为
$\left. \frac{\partial \mathbf{r}(\mathbf{x}_1)}{\partial \mathbf{x}_1} \right|_{\mathbf{m}} = \left. \begin{bmatrix} \frac{\partial (x - m_x) }{\partial x } & \frac{\partial (x - m_x) }{\partial y } & \frac{\partial (x - m_x) }{\partial \theta }\\ \frac{\partial (y - m_y) }{\partial x } & \frac{\partial (y - m_y) }{\partial y } & \frac{\partial (y - m_y) }{\partial \theta } \end{bmatrix}\right|_{x=m_x, y=m_y} = \begin{bmatrix}1 &0 &0\\ 0 & 1 &0\end{bmatrix}$
在该一元测量中 $\theta$ 分量并不起作用, 只是为了兼容其他因子 (如 Odometry 因子) 才引入的.

构建因子时需要明确误差和 Jacobian, 是由于因子图的构建是为了求解非线性二乘问题.

#include "gtsam/geometry/Pose2.h"
#include "gtsam/geometry/Point2.h"
#include "gtsam/slam/BetweenFactor.h"
#include "gtsam/slam/BearingRangeFactor.h"
#include "gtsam/nonlinear/NonlinearFactorGraph.h"
#include "gtsam/nonlinear/LevenbergMarquardtOptimizer.h"
#include "gtsam/nonlinear/Marginals.h"
#include "gtsam/inference/Symbol.h"
#include "Eigen/Dense"
#include "iostream"

// 自定义因子 UnaryFactor 继承自 NoiseModelFactorN
class UnaryFactor: public gtsam::NoiseModelFactorN<gtsam::Pose2> {
    double mx_, my_; // mx_, my_ 代表测量到的数值

 public:
    typedef boost::shared_ptr<UnaryFactor> shared_ptr;
    // The constructor requires the variable key, the (X, Y) measurement value, and the noise model
    UnaryFactor(gtsam::Key k, double x, double y, const gtsam::SharedNoiseModel& model):
    gtsam::NoiseModelFactorN<gtsam::Pose2>(model, k), mx_(x), my_(y) {}  // 利用 key 和 noise model 初始化基类 NoiseModelFactorN
    ~UnaryFactor() override {}

    // evaluateError 中建立 (1)误差向量相对于状态变量的Jacobian 和 (2) 误差向量
    gtsam::Vector evaluateError(const gtsam::Pose2& q, 
    boost::optional<gtsam::Matrix&> H = boost::none) const override {
        if (H) (*H) = (gtsam::Matrix(2, 3) <<
                1.0, 0.0, 0.0,
                0.0, 1.0, 0.0).finished();
        return (gtsam::Vector(2) << q.x() - mx_, q.y() - my_).finished();
    }
};


int main(int argc, char** argv)
{
    gtsam::NonlinearFactorGraph graph;

    auto x_1 = gtsam::Symbol('x', 1);
    auto x_2 = gtsam::Symbol('x', 2);
    auto x_3 = gtsam::Symbol('x', 3);
    auto l_1 = gtsam::Symbol('l', 1);
    auto l_2 = gtsam::Symbol('l', 2);

    // std::freopen("results.txt", "w", stdout);  // 输出重定位

    // 第一部分 因子图的构建
    // factor 1 —— prior factor for the starting point x_1 起始点先验因子
    // x_1 变量的类型为 gtsam::Pose2
    gtsam::Pose2 startingPriorMean(0.0, 0.0, 0.0);
    auto startingPriorNoise = gtsam::noiseModel::Diagonal::Sigmas(Eigen::Vector3d(0.2, 0.2, 0.1));
    graph.addPrior(x_1, startingPriorMean, startingPriorNoise);

    // factor 2 and 3 —— odometry factors for x_1->x_2 and x_2->x_3 里程计因子
    // x_2 和 x_3 变量的类型都为 gtsam::Pose2
    gtsam::Pose2 odometry1(2.0, 0.0, 0.0);
    auto odometryNoise = gtsam::noiseModel::Diagonal::Sigmas(Eigen::Vector3d(0.25, 0.25, 0.1));
    graph.add(gtsam::BetweenFactor<gtsam::Pose2>(x_1, x_2, odometry1, odometryNoise));
    graph.add(gtsam::BetweenFactor<gtsam::Pose2>(x_2, x_3, odometry1, odometryNoise));

    // factor 4 and 5 —— prior factors for landmark l_1 and l_2 路标先验因子
    // l_1 和 l_2 变量的类型都为 gtsam::Point2
    gtsam::Point2 landmarkPriorMean1(2.0, 2.0);
    gtsam::Point2 landmarkPriorMean2(4.0, 2.0);
    auto landmarkPriorNoise = gtsam::noiseModel::Diagonal::Sigmas(Eigen::Vector2d(0.2, 0.2));
    graph.add(gtsam::PriorFactor<gtsam::Point2>(l_1, landmarkPriorMean1, landmarkPriorNoise));
    graph.add(gtsam::PriorFactor<gtsam::Point2>(l_2, landmarkPriorMean2, landmarkPriorNoise));

    // factor 6 —— unary measurement factor for x_1 起始点的一元测量, 与先验因子的区别是信息维度 (少了方向数据)
    auto startingUnaryNoise = gtsam::noiseModel::Diagonal::Sigmas(Eigen::Vector2d(0.1, 0.1));
    // 自定义因子的 noise model 的维度须与自定义因子中的误差向量维度一致
    // graph.add(boost::make_shared<UnaryFactor>(x_1, 0.0, 0.0, startingPriorNoise));
    graph.emplace_shared<UnaryFactor>(x_1, 0.01, 0.01, startingUnaryNoise);

    // factor 7 - binary measurement factor for (x_1, l_1) 二元测量
    // l_1 在 x_1 局部坐标系中的测量值
    auto measurementNoise = gtsam::noiseModel::Diagonal::Sigmas(Eigen::Vector2d(0.1, 0.2));
    gtsam::Rot2 bearing_x1_l1 = gtsam::Rot2::fromAngle(M_PI/4);
    double range_x1_l1 = sqrt(8.0);
    graph.add(gtsam::BearingRangeFactor<gtsam::Pose2, gtsam::Point2>(x_1, l_1, bearing_x1_l1, range_x1_l1, measurementNoise));

    // factor 8 - binary measurement factor for (x_2, l_1) 二元测量
    // l_1 在 x_2 局部坐标系中的测量值
    gtsam::Rot2 bearing_x2_l1 = gtsam::Rot2::fromAngle(M_PI/2);
    double range_x2_l1 = 2.0;
    graph.add(gtsam::BearingRangeFactor<gtsam::Pose2, gtsam::Point2>(x_2, l_1, bearing_x2_l1, range_x2_l1, measurementNoise));

    // factor 9 - binary measurement factor for (x_3, l_2) 二元测量
    // l_2 在 x_3 局部坐标系中的测量值
    gtsam::Rot2 bearing_x3_l2 = gtsam::Rot2::fromAngle(M_PI/2);
    double range_x3_l2 = 2.0;
    graph.add(gtsam::BearingRangeFactor<gtsam::Pose2, gtsam::Point2>(x_3, l_2, bearing_x3_l2, range_x3_l2, measurementNoise));

    graph.print("\nFactor Graph\n");  // 因子图构建的输出

    // 第二部分 非线性优化计算
    printf("Nonlinear optimization:\n");
    gtsam::Values initial;  // 一些随机值作为非线性二乘问题迭代计算的初始值, 是对真值的初步猜测, 与真值之间有偏差
    initial.insert(x_1, gtsam::Pose2(0.0, 0.1, 0.1));
    initial.insert(x_2, gtsam::Pose2(0.17, -0.1, -0.05));
    initial.insert(x_3, gtsam::Pose2(0.45, 0.1, 0.1));
    initial.insert(l_1, gtsam::Point2(0.19, 0.21));
    initial.insert(l_2, gtsam::Point2(42.0, 19.0));
    initial.print("Initial estimation:"); // 初始值的输出

    // gtsam::Values result = gtsam::LevenbergMarquardtOptimizer(graph, initial).optimize();
    // result.print("Final results:"); // 优化值的输出
    gtsam::LevenbergMarquardtParams parameters;
    parameters.setVerbosity("ERROR");
    // parameters.setVerbosityLM("SUMMARY");
    gtsam::LevenbergMarquardtOptimizer optimizer(graph, initial, parameters);
    gtsam::Values result = optimizer.optimize();
    result.print("\nFinal Result:\n");

    // 第三部分 边缘概率计算
    std::cout.precision(3);
    printf("\nMarginal Covariance:\n");
    gtsam::Marginals marginals(graph, result);
    std::cout << "\nx1 covariance:\n" << marginals.marginalCovariance(x_1) << std::endl;
    std::cout << "\nx2 covariance:\n" << marginals.marginalCovariance(x_2) << std::endl;
    std::cout << "\nx3 covariance:\n" << marginals.marginalCovariance(x_3) << std::endl;
    std::cout << "\nl1 covariance:\n" << marginals.marginalCovariance(l_1) << std::endl;
    std::cout << "\nl2 covariance:\n" << marginals.marginalCovariance(l_2) << std::endl;

}

2. CMakeLists.txt 脚本

cmake_minimum_required(VERSION 3.0)

project(factor_graph_example)
find_package(GTSAM 4.2 REQUIRED COMPONENTS)
include_directories(${GTSAM_INCLUDE_DIR})

FILE(GLOB_RECURSE HPP_INCLUDE include/*.hpp include/*.h)
FILE(GLOB_RECURSE CPP_SOURCE source/*.cpp)
add_executable(${CMAKE_PROJECT_NAME} ${CPP_SOURCE} ${HPP_INCLUDE})
target_link_libraries(${CMAKE_PROJECT_NAME} gtsam)

3. 数值结果

Factor Graph
size: 9

Factor 0: PriorFactor on x1
  prior mean:  (0, 0, 0)
  noise model: diagonal sigmas [0.2; 0.2; 0.1];

Factor 1: BetweenFactor(x1,x2)
  measured:  (2, 0, 0)
  noise model: diagonal sigmas [0.25; 0.25; 0.1];

Factor 2: BetweenFactor(x2,x3)
  measured:  (2, 0, 0)
  noise model: diagonal sigmas [0.25; 0.25; 0.1];

Factor 3: PriorFactor on l1
  prior mean: [
        2;
        2
]
isotropic dim=2 sigma=0.2

Factor 4: PriorFactor on l2
  prior mean: [
        4;
        2
]
isotropic dim=2 sigma=0.2

Factor 5:   keys = { x1 }
isotropic dim=2 sigma=0.1

Factor 6: BearingRangeFactor
Factor 6:   keys = { x1 l1 }
  noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 0.785398163
range  2.82842712

Factor 7: BearingRangeFactor
Factor 7:   keys = { x2 l1 }
  noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 1.57079633
range  2

Factor 8: BearingRangeFactor
Factor 8:   keys = { x3 l2 }
  noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 1.57079633
range  2

Nonlinear optimization:
Initial estimation:
Values with 5 values:
Value l1: (Eigen::Matrix<double, 2, 1, 0, 2, 1>)
[
        0.19;
        0.21
]

Value l2: (Eigen::Matrix<double, 2, 1, 0, 2, 1>)
[
        42;
        19
]

Value x1: (gtsam::Pose2)
(0, 0.1, 0.1)

Value x2: (gtsam::Pose2)
(0.17, -0.1, -0.05)

Value x3: (gtsam::Pose2)
(0.45, 0.1, 0.1)

Initial error: 45816.3375
newError: 60.0746132
errorThreshold: 60.0746132 > 0
absoluteDecrease: 45756.2629219 >= 1e-05
relativeDecrease: 0.99868879495 >= 1e-05
newError: 1.24368959022
errorThreshold: 1.24368959022 > 0
absoluteDecrease: 58.8309235801 >= 1e-05
relativeDecrease: 0.97929758471 >= 1e-05
newError: 0.00598271925373
errorThreshold: 0.00598271925373 > 0
absoluteDecrease: 1.23770687096 >= 1e-05
relativeDecrease: 0.995189539817 >= 1e-05
newError: 0.00296591263207
errorThreshold: 0.00296591263207 > 0
absoluteDecrease: 0.00301680662167 >= 1e-05
relativeDecrease: 0.504253416167 >= 1e-05
newError: 0.00296590504323
errorThreshold: 0.00296590504323 > 0
absoluteDecrease: 7.58883373286e-09 < 1e-05
relativeDecrease: 2.55868418065e-06 < 1e-05
converged
errorThreshold: 0.00296590504323 <? 0
absoluteDecrease: 7.58883373286e-09 <? 1e-05
relativeDecrease: 2.55868418065e-06 <? 1e-05
iterations: 5 >? 100

Final Result:

Values with 5 values:
Value l1: (Eigen::Matrix<double, 2, 1, 0, 2, 1>)
[
        2.00402979248;
        2.00353272869
]

Value l2: (Eigen::Matrix<double, 2, 1, 0, 2, 1>)
[
        4.00101280265;
        2.00108370699
]

Value x1: (gtsam::Pose2)
(0.00699225259677, 0.00707591845494, -0.000329623653647)

Value x2: (gtsam::Pose2)
(2.00448395483, 0.00399757524079, -6.886908946e-05)

Value x3: (gtsam::Pose2)
(4.00290058662, 0.00216735620844, 0.000437767142559)


Marginal Covariance:

x1 covariance:
  0.00728 -0.000291  0.000719
-0.000291   0.00737  -0.00105
 0.000719  -0.00105   0.00438

x2 covariance:
   0.0397  -0.00156   0.00895
 -0.00156    0.0315 -0.000391
  0.00895 -0.000391   0.00798

x3 covariance:
 0.0701   0.012  0.0193
  0.012  0.0546 0.00783
 0.0193 0.00783  0.0147

l1 covariance:
  0.0224 -0.00333
-0.00333   0.0217

l2 covariance:
   0.0329 -0.000904
-0.000904    0.0336

IV. 基于 GTSAM 的因子图实例的 Python 实现

1. Python 源码

同样地, 难点在于一元测量因子的自定义构建.

Python 上运行画图比较方便.

"""
GTSAM Copyright 2010-2018, Georgia Tech Research Corporation,
Atlanta, Georgia 30332-0415
All Rights Reserved
Authors: Frank Dellaert, et al. (see THANKS for the full author list)

See LICENSE for the license information

Simple robotics example using odometry measurements and bearing-range (laser) measurements
Author: Alex Cunningham (C++), Kevin Deng & Frank Dellaert (Python)

++ + custom factor of the unary measurement 

"""
# pylint: disable=invalid-name, E1101

from __future__ import print_function
from functools import partial
from typing import List, Optional

import gtsam
import numpy as np
from gtsam.symbol_shorthand import L, X
import gtsam.utils.plot as gtsam_plot
import matplotlib.pyplot as plt

# Create noise models
PRIOR_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.2, 0.2, 0.1]))
ODOMETRY_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.25, 0.25, 0.1]))
MEASUREMENT_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.1, 0.2]))
UNARY_MEASUREMENT_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.1, 0.1]))
LANDMARK_PRIOR_NOISE = gtsam.noiseModel.Diagonal.Sigmas(np.array([0.2, 0.2]))


def error_unary(measurement: np.ndarray, this: gtsam.CustomFactor,
              values: gtsam.Values,
              jacobians: Optional[List[np.ndarray]]) -> float:
    """Unary Factor error function
    :param measurement: Unary measurement, to be filled with `partial`
    :param this: gtsam.CustomFactor handle
    :param values: gtsam.Values
    :param jacobians: Optional list of Jacobians
    :return: the unwhitened error
    """
    key = this.keys()[0]
    estimate = values.atPose2(key)
    # error = [estimate[0], estimate[1]] - measurement
    error = [(estimate.x() - measurement[0]), (estimate.y() - measurement[1])]
    
    print(error)

    if jacobians is not None:
        jacobians[0] = np.matrix([[1.0, 0.0, 0.0], [0.0, 1.0, 0.0]])
    # jacobians[0] = np.eye(2)

    return error
            


def main():
    """Main runner"""

    # Create an empty nonlinear factor graph
    graph = gtsam.NonlinearFactorGraph()

    # Create the keys corresponding to unknown variables in the factor graph
    X1 = X(1)
    X2 = X(2)
    X3 = X(3)
    L1 = L(1)
    L2 = L(2)



    # Add a prior on pose X1 at the origin. A prior factor consists of a mean and a noise model
    graph.add(
        gtsam.PriorFactorPose2(X1, gtsam.Pose2(0.0, 0.0, 0.0), PRIOR_NOISE))

    # Add odometry factors between X1,X2 and X2,X3, respectively
    graph.add(
        gtsam.BetweenFactorPose2(X1, X2, gtsam.Pose2(2.0, 0.0, 0.0),
                                 ODOMETRY_NOISE))
    graph.add(
        gtsam.BetweenFactorPose2(X2, X3, gtsam.Pose2(2.0, 0.0, 0.0),
                                 ODOMETRY_NOISE))
    


    # Add a prior on pose L1 at the origin. A prior factor consists of a mean and a noise model
    landmarkPriorMean1 = gtsam.Point2(2.0, 2.0)
    graph.add(
        gtsam.PriorFactorPoint2(L1, landmarkPriorMean1, LANDMARK_PRIOR_NOISE))


    # Add a prior on pose L2 at the origin. A prior factor consists of a mean and a noise model
    landmarkPriorMean1 = gtsam.Point2(4.0, 2.0)
    graph.add(
        gtsam.PriorFactorPoint2(L2, landmarkPriorMean1, LANDMARK_PRIOR_NOISE))


    # Add the Unary-Measurement factors on X1
    measurement = [0.01 , 0.01]
    graph.add(
        gtsam.CustomFactor(UNARY_MEASUREMENT_NOISE, [X1], partial(error_unary, measurement)))
    # 注意 此处 functools.partial 基于error_unary 函数创建可调用对象, 把原函数中的第一个参数 measurement 固定了
    # 直白一点就是 传递了 measurement 参数值
    # 不要误解为偏微分计算

    # Add Range-Bearing measurements to two different landmarks L1 and L2
    graph.add(
        gtsam.BearingRangeFactor2D(X1, L1, gtsam.Rot2.fromDegrees(45),
                                   np.sqrt(4.0 + 4.0), MEASUREMENT_NOISE))
    graph.add(
        gtsam.BearingRangeFactor2D(X2, L1, gtsam.Rot2.fromDegrees(90), 2.0,
                                   MEASUREMENT_NOISE))
    graph.add(
        gtsam.BearingRangeFactor2D(X3, L2, gtsam.Rot2.fromDegrees(90), 2.0,
                                   MEASUREMENT_NOISE))

    # Print graph
    print("Factor Graph:\n{}".format(graph))

    # Create (deliberately inaccurate) initial estimate
    initial_estimate = gtsam.Values()
    initial_estimate.insert(X1, gtsam.Pose2(0.0, 0.1, 0.1))
    initial_estimate.insert(X2, gtsam.Pose2(0.17, -0.1, -0.05))
    initial_estimate.insert(X3, gtsam.Pose2(0.45, 0.10, 0.10))
    initial_estimate.insert(L1, gtsam.Point2(0.19, 0.21))
    initial_estimate.insert(L2, gtsam.Point2(42.0, 19.0))

    # Print
    print("Initial Estimate:\n{}".format(initial_estimate))

    # Optimize using Levenberg-Marquardt optimization. The optimizer
    # accepts an optional set of configuration parameters, controlling
    # things like convergence criteria, the type of linear system solver
    # to use, and the amount of information displayed during optimization.
    # Here we will use the default set of parameters.  See the
    # documentation for the full set of parameters.
    params = gtsam.LevenbergMarquardtParams()
    params.setVerbosity("ERROR")
    optimizer = gtsam.LevenbergMarquardtOptimizer(graph, initial_estimate,
                                                  params)
    result = optimizer.optimize()
    print("\nFinal Result:\n{}".format(result))

    # Calculate and print marginal covariances for all variables
    marginals = gtsam.Marginals(graph, result)
    for (key, s) in [(X1, "X1"), (X2, "X2"), (X3, "X3"), (L1, "L1"),
                     (L2, "L2")]:
        print("{} covariance:\n{}\n".format(s,
                                            marginals.marginalCovariance(key)))
        
    for (key, s) in [(X1, "X1"), (X2, "X2"), (X3, "X3") ]:
        gtsam_plot.plot_pose2(0, result.atPose2(key), 0.5, marginals.marginalCovariance(key))
    for (key, s) in [ (L1, "L1"),(L2, "L2") ]:
        gtsam_plot.plot_point2(0, result.atPoint2(key), 0.5, marginals.marginalCovariance(key))
    plt.axis('equal')
    plt.show()


if __name__ == "__main__":
    main()

2. 数值结果

可以看出不管是 C++ 版本的结果还是 Python 版本的结果是一致的.

Factor Graph:
NonlinearFactorGraph: size: 9

Factor 0: PriorFactor on x1
  prior mean:  (0, 0, 0)
  noise model: diagonal sigmas [0.2; 0.2; 0.1];

Factor 1: BetweenFactor(x1,x2)
  measured:  (2, 0, 0)
  noise model: diagonal sigmas [0.25; 0.25; 0.1];

Factor 2: BetweenFactor(x2,x3)
  measured:  (2, 0, 0)
  noise model: diagonal sigmas [0.25; 0.25; 0.1];

Factor 3: PriorFactor on l1
  prior mean: [
	2;
	2
]
isotropic dim=2 sigma=0.2

Factor 4: PriorFactor on l2
  prior mean: [
	4;
	2
]
isotropic dim=2 sigma=0.2

Factor 5: CustomFactor on x1
isotropic dim=2 sigma=0.1

Factor 6: BearingRangeFactor
Factor 6:   keys = { x1 l1 }
  noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 0.785398163
range  2.82842712

Factor 7: BearingRangeFactor
Factor 7:   keys = { x2 l1 }
  noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 1.57079633
range  2

Factor 8: BearingRangeFactor
Factor 8:   keys = { x3 l2 }
  noise model: diagonal sigmas [0.1; 0.2];
ExpressionFactor with measurement: bearing : 1.57079633
range  2


Initial Estimate:
Values with 5 values:
Value l1: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
	0.19;
	0.21
]

Value l2: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
	42;
	19
]

Value x1: (gtsam::Pose2)
(0, 0.1, 0.1)

Value x2: (gtsam::Pose2)
(0.17, -0.1, -0.05)

Value x3: (gtsam::Pose2)
(0.45, 0.1, 0.1)


[-0.01, 0.09000000000000001]
Initial error: 45816.3375
[-0.01, 0.09000000000000001]
[-0.09431931375291222, 0.08073185880549684]
newError: 60.0746132
errorThreshold: 60.0746132 > 0
absoluteDecrease: 45756.2629219 >= 1e-05
relativeDecrease: 0.99868879495 >= 1e-05
[-0.09431931375291222, 0.08073185880549684]
[-0.021338603719452405, -0.0190455547054151]
newError: 1.24368959022
errorThreshold: 1.24368959022 > 0
absoluteDecrease: 58.8309235801 >= 1e-05
relativeDecrease: 0.97929758471 >= 1e-05
[-0.021338603719452405, -0.0190455547054151]
[-0.0026978140729723103, -0.0029251685355443906]
newError: 0.00598271925373
errorThreshold: 0.00598271925373 > 0
absoluteDecrease: 1.23770687096 >= 1e-05
relativeDecrease: 0.995189539817 >= 1e-05
[-0.0026978140729723103, -0.0029251685355443906]
[-0.0030085387600294784, -0.002923210421981185]
newError: 0.00296591263207
errorThreshold: 0.00296591263207 > 0
absoluteDecrease: 0.00301680662167 >= 1e-05
relativeDecrease: 0.504253416167 >= 1e-05
[-0.0030085387600294784, -0.002923210421981185]
[-0.0030077474032272995, -0.0029240815450598734]
newError: 0.00296590504323
errorThreshold: 0.00296590504323 > 0
absoluteDecrease: 7.58883373286e-09 < 1e-05
relativeDecrease: 2.55868418065e-06 < 1e-05
converged
errorThreshold: 0.00296590504323 <? 0
absoluteDecrease: 7.58883373286e-09 <? 1e-05
relativeDecrease: 2.55868418065e-06 <? 1e-05
iterations: 5 >? 100

Final Result:
Values with 5 values:
Value l1: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
	2.00402979248;
	2.00353272869
]

Value l2: (Eigen::Matrix<double, -1, 1, 0, -1, 1>)
[
	4.00101280265;
	2.00108370699
]

Value x1: (gtsam::Pose2)
(0.00699225259677, 0.00707591845494, -0.000329623653647)

Value x2: (gtsam::Pose2)
(2.00448395483, 0.00399757524079, -6.886908946e-05)

Value x3: (gtsam::Pose2)
(4.00290058662, 0.00216735620844, 0.000437767142559)


[-0.0030077474032272995, -0.0029240815450598734]
X1 covariance:
[[ 0.00728256 -0.00029085  0.0007187 ]
 [-0.00029085  0.0073673  -0.00104787]
 [ 0.0007187  -0.00104787  0.0043819 ]]

X2 covariance:
[[ 0.03966749 -0.00155955  0.00895399]
 [-0.00155955  0.03147331 -0.00039051]
 [ 0.00895399 -0.00039051  0.00797534]]

X3 covariance:
[[0.07007273 0.01202848 0.01925868]
 [0.01202848 0.05455565 0.00783016]
 [0.01925868 0.00783016 0.01468828]]

L1 covariance:
[[ 0.02237142 -0.00332628]
 [-0.00332628  0.02172322]]

L2 covariance:
[[ 0.03294629 -0.00090407]
 [-0.00090407  0.03363416]]