CF1468J Road Reform 题解

link

CF1468J Road Reform

题面翻译

给定一个有 $n$ 个节点，$m$ 条无向带权边的图，和一个参数 $k$，第 $i$ 条边权值为 $s_i$。

现在你要保留这个图中的 $n-1$ 条边使得这个图变成一棵树，然后你可以对这棵树上的任意边进行修改，每次修改可以使这个边的权值加上一或减去一。

现在你需要使所有边权的最大值正好等于 $k$，求所有保留方案的最小操作数。

$T$ 组询问。

保证初始时给定的图满足任意两个点互相可达，没有重边或自环。

$1\le T\le 10^3.$

$1\le n\le 2\times 10^5;n-1\le m\le \min (\frac{n(n+1)}{2},2\times 10^5);$

$\sum n,\sum m\le 2\times 10^5;$

$1\le k,s_i\le 10^9.$

题目描述

There are $n$ cities and $m$ bidirectional roads in Berland. The $i$ -th road connects the cities $x_i$ and $y_i$ , and has the speed limit $s_i$ . The road network allows everyone to get from any city to any other city.

The Berland Transport Ministry is planning a road reform.

First of all, maintaining all $m$ roads is too costly, so $m-(n-1)$ roads will be demolished in such a way that the remaining $(n-1)$ roads still allow to get to any city from any other city. Formally, the remaining roads should represent an undirected tree.

Secondly, the speed limits on the remaining roads might be changed. The changes will be done sequentially, each change is either increasing the speed limit on some road by $1$ , or decreasing it by $1$ . Since changing the speed limit requires a lot of work, the Ministry wants to minimize the number of changes.

The goal of the Ministry is to have a road network of $(n-1)$ roads with the maximum speed limit over all roads equal to exactly $k$ . They assigned you the task of calculating the minimum number of speed limit changes they have to perform so the road network meets their requirements.

For example, suppose the initial map of Berland looks like that, and $k=7$ :

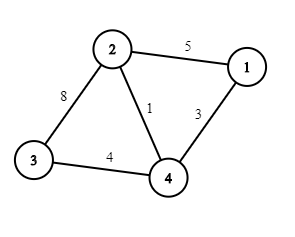Then one of the optimal courses of action is to demolish the roads $1$ – $4$ and $3$ – $4$ , and then decrease the speed limit on the road $2$ – $3$ by $1$ , so the resulting road network looks like that:

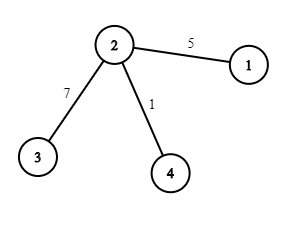
输入格式

The first line contains one integer $t$ ( $1\le t\le 1000$ ) — the number of test cases.

The first line of each test case contains three integers $n$ , $m$ and $k$ ( $2\le n\le 2\cdot 10^5$ ; $n-1\le m\le \min (2\cdot 10^5,\frac{n(n-1)}{2})$ ; $1\le k\le 10^9$ ) — the number of cities, the number of roads and the required maximum speed limit, respectively.

Then $ m $ lines follow. The $ i $ -th line contains three integers $x_i$ , $y_i$ and $s_i$ ( $1\le x_i,y_i\le n$ ; $x_i\ne y_i$ ; $1\le s_i\le 10^9$ ) — the cities connected by the $i$ -th road and the speed limit on it, respectively. All roads are bidirectional.

The road network in each test case is connected (that is, it is possible to reach any city from any other city by traveling along the road), and each pair of cities is connected by at most one road.

The sum of $ n $ over all test cases does not exceed $2\cdot 10^5$ . Similarly, the sum of $m$ over all test cases does not exceed $2\cdot 10^5$ .

输出格式

For each test case, print one integer — the minimum number of changes the Ministry has to perform so that the maximum speed limit among the remaining $(n-1)$ roads is exactly $k$ .

样例 #1

样例输入 #1

4
4 5 7
4 1 3
1 2 5
2 3 8
2 4 1
3 4 4
4 6 5
1 2 1
1 3 1
1 4 2
2 4 1
4 3 1
3 2 1
3 2 10
1 2 8
1 3 10
5 5 15
1 2 17
3 1 15
2 3 10
1 4 14
2 5 8

样例输出 #1

1
3
0
0

提示

The explanation for the example test:

The first test case is described in the problem statement.

In the second test case, the road network initially looks like that:

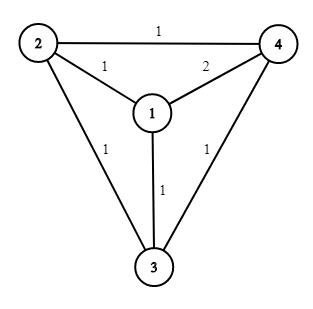The Ministry can demolish the roads $1$ – $2$ , $3$ – $2$ and $3$ – $4$ , and then increase the speed limit on the road $1$ – $4$ three times.

In the third test case, the road network already meets all the requirements.

In the fourth test case, it is enough to demolish the road $1$ – $2$ so the resulting road network meets the requirements.

算法：最小生成树

思路：
首先看题。

题目中说：要在图中保留 $n-1$ 条边，使它变成一棵树。

因此想到 最小生成树。

我这里用的是 Kruskal，需要用到并查集。

因此要注意并查集要初始化！

大家应该都知道 Kruskal 算法的流程是：先对边权从小到大排序，再枚举每一个 $i$，看一下所对应的 $u$ 和 $v$ 是否在同一个集合内。如果不是，就可以选择这一条边。

做完最小生成树以后，我们要进行分类讨论：

计最小生成树中最大的边权为 $t$。

当 $t<k$ 时，遍历所有边，取与$k$ 差值最小的即可。

当 $t>k$ 时，将所有边权与 $k$ 的差值相加即可。

注意多测要清空即可。

代码：

#include<bits/stdc++.h>
using namespace std;
#define ll long long
const ll N=4e5+10,inf=2e9;
ll T,n,m,k,t,ans,ct,fa[N];
struct E{
    ll u,v,w;
}a[N];
bool cmp(E l,E r){
    return l.w<r.w;
}
void jian(){
    for(int i=1;i<=n;i++) fa[i]=i;
}
ll getfa(ll x){
    return fa[x]==x?x:fa[x]=getfa(fa[x]);
}
void kruskal(){
    jian();ct=t=ans=0;//多测不清空，爆零两行泪！
    sort(a+1,a+m+1,cmp);
    for(int i=1;i<=m;i++){
        ll x=getfa(a[i].u),y=getfa(a[i].v);
        if(x==y) continue;
        t=a[i].w,ans+=max(t-k,0ll),fa[x]=y;
        //因为边权是从小到大枚举的，所以当前值一定是最大的
    }
}
int main(){
    ios::sync_with_stdio(false);cin.tie(0);cout.tie(0);
    cin>>T;
    while(T--){
        cin>>n>>m>>k;
        for(int i=1;i<=m;i++)
            cin>>a[i].u>>a[i].v>>a[i].w;
        kruskal();
        if(t<k){
            ans=inf;//不要忘记
            for(int i=1;i<=m;i++)
                ans=min(ans,abs(a[i].w-k));
        }//t>k的情况在做最小生成树的时候顺便求出来了
        cout<<ans<<"\n";
    }
    return 0;
}