Deep Layer Aggregation（CVPR 2018）原理与代码解析

paper：Deep Layer Aggregation

official implementation：https://github.com/ucbdrive/dla

third-party implementation：https://github.com/huggingface/pytorch-image-models/blob/main/timm/models/dla.py

本文的创新点

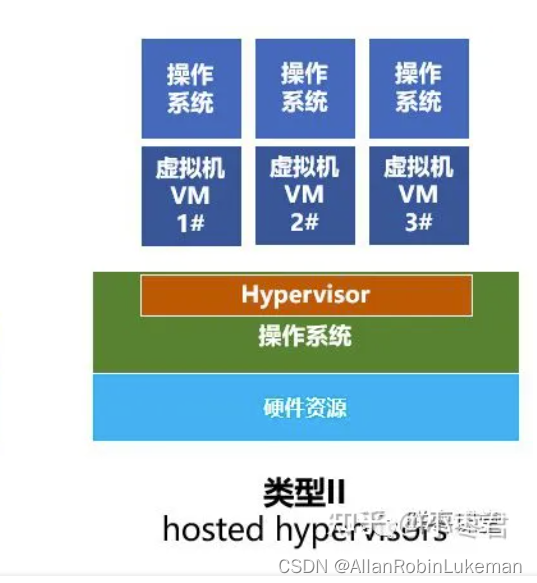
骨干网络的设计主要关注于设计出更深更宽的网络，但是如何更好的聚合不同layer和block的信息缺乏足够的关注。虽然skip connection已经被用来组合不同的网络层，但这些连接本身都是“浅层的”并且只是通过简单的单步操作进行融合。本文通过更深层的聚合来更好的实现跨层信息的融合，提出了深层聚合结构deep layer aggregation，通过迭代、分层级的合并特征，使得网络具有更高的精度以及更少的参数。

方法介绍

Iterative Deep Aggregation

迭代的深度聚合遵循骨干架构迭代堆叠的方式，根据特征分辨率将网络stacked blocks划分为不同的stage，更深的stage语义信息更丰富但空间信息更粗糙。skip connection从浅层到深层合并尺度和分辨率。但是现有网络中的跳跃连接如FCN、U-Net、FPN是线性的并且浅层的信息聚合的最少，如图2(b)所示

本文提出逐步progressively聚合并用IDA加深表示。聚合从最浅、最小尺度开始迭代的合并更深、更大的尺度。通过这种方式，浅层特征传播到不同聚合阶段并得到细化refined。IDA的结构如图2(c)所示

Hierarchical Deep Aggregation

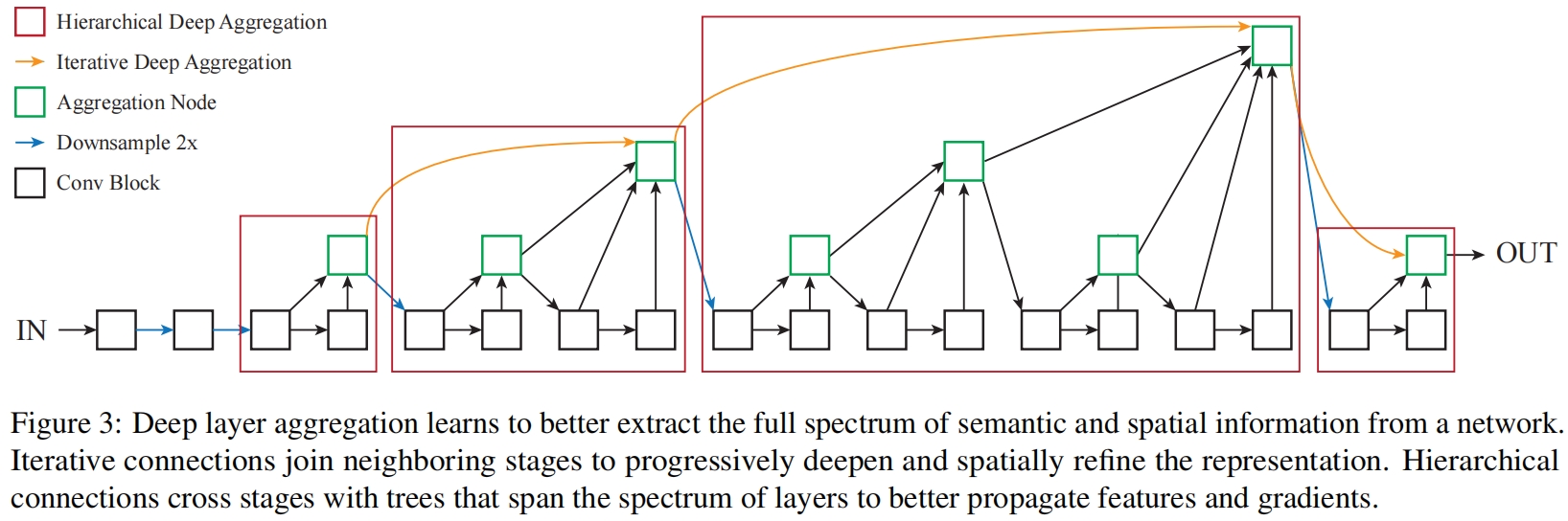
层级深度聚合合并树tree中的block和stage来保持与合并特征通道。通过HDA，浅层和深层被组合起来学习跨越更多特征层级的更丰富的组合。尽管IDA有效的结合了各个stage，但仍不足以融合网络了多个block因为它是按顺序的。层级聚合的深层、分支结构如图2(d)所示

在构建了HDA的通用结构后我们可以进一步优化深度和效率。不是仅仅将中间聚合传送到树的上层，相反作者将一个聚合节点的输出传回到backbone作为下一个子树的输入，如图2(e)所示。这种方式传播了所有之前的block而不仅仅是前一个单独的block，从而更好的保存的特征。为了提高效率，作者合并了相同深度的聚合节点（合并父节点和左子节点）如图2(f)所示，这样就得到了最终的结构。

Architectural Elements

Aggregation Nodes 聚合节点的主要作用是组合和压缩输入。节点学习挑选和映射重要的信息来保持输出与单个输入相同的维度。IDA节点的参数总是两个，而HDA的参数数量取决于树的深度。

尽管聚合节点可以是任何block或layer，但为了简单和效率作者只用了一个卷积接一个BN和非线性层。在分类网络中，所有的节点都使用1x1卷积。在语义分割网络中，作者额外添加了一个层级的迭代深度聚合来进行特征插值，这里使用3x3卷积。

残差连接对于组合非常深的网络非常重要，我们也可以在聚合节点中加入残差连接。但它们对于聚合是否有必要还不清楚。使用HDA，任何block到root的最短路径最大是层级结构的深度，因此沿着聚合路径不太可能出现梯度消失或梯度爆炸。作者通过实验发现当最深的层级有4层或更多时节点中的残差连接对HDA有帮助，而对于更小的层级可能会伤害网络。

Blocks and Stages 深层聚合是一个通用结构，可以与任何backbone兼容，因此对block和stage的内部结构没有要求。

作者在实验中用了三种不同类型的residual block，Basic block、Bottleneck block、Split block。

Applications

Classification Networks

作者用IDA和HDA增强了ResNet和ResNeXt，它们都是划分了stage的网络，即根据分辨率对block进行了分组，每个block内包含残差连接。每个stage结束分辨率减半，一共6个stage，第一阶段保持输入分辨率，最后一个阶段下采样32x。最后的特征图通过全局平均池化接一个线性层，最后通过softmax得到预测结果。

我们用IDA进行跨stage连接，并用HDA进行stage内部和跨stage的连接。通过共享聚合节点可以很容易的进行聚合，只需要在每个层级更换根节点。每个stage通过size=2, stride=2的max pooling进行下采样。

最前面的stage有单独的结构。和DRN一样，在stage1-2中，作者用strided卷积替换max pooling。stage1包括一个7x7的卷积和一个basic block，stage2只包含一个basic block。在其它的stage中，组合使用IDA和HDA。

为了直接比较不同网络中的层和参数，作者构建了和ResNet-34、ResNet-50、ResNet-101层数相同的网络，具体如表1所示。

Dense Prediction Networks

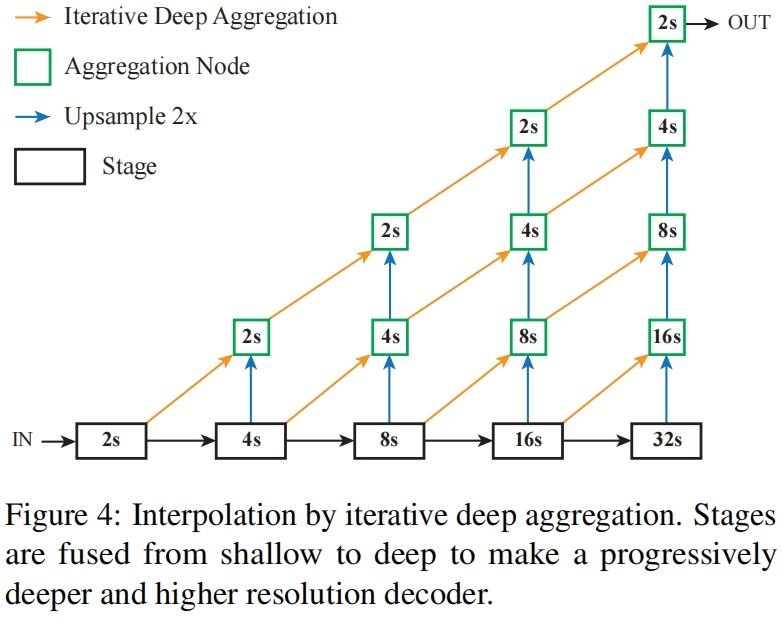
语义分割、轮廓检测和其他image-to-image的任务可以利用聚合来融合局部和全局信息。从分类DLA到全卷积DLA的转换很简单和其它结构没什么区别。我们利用插值以及IDA的增强来得到需要的输出分辨率。

如图4所示，用于插值的IDA通过投影和上采样增加了深度和分辨率。所有的投影和上采样参数是在网络优化过程中学习到的。上采样初始化为双线性插值然后可以像FCN中一样进行学习。首先将stage3-6的输出映射为32通道，然后插值到和stage2同样的分辨率。然后迭代的聚合这些stage来学习低级和高级特征的深度融合。虽然聚合与FCN中的skip connection、hypercolumn features、FPN的top-down connection的目的相同，但具体的方法不同，聚合从浅到深进一步细化特征。注意这里IDA用了两次，一次在backbone用于connect stages，一次用于恢复分辨率。

代码解析

这里以timm中的实现为例介绍一下代码，我们可以用预训练模型测试自己的图片，测试代码如下

from PIL import Image
from timm.data import resolve_data_config
from timm.data.transforms_factory import create_transform
import torch

import timm

model = timm.create_model('dla34', pretrained=True)
model.eval()

config = resolve_data_config({}, model=model)
transform = create_transform(**config)

filename = '/disk1/tmp/test.jpg'
img = Image.open(filename).convert('RGB')
tensor = transform(img).unsqueeze(0)  # transform and add batch dimension

with torch.no_grad():
    out = model(tensor)
probabilities = torch.nn.functional.softmax(out[0], dim=0)
print(probabilities.shape)  # torch.Size([1000])

这里调用的是'dla34'，如下，对应表1中DLA-34的配置

@register_model
def dla34(pretrained=False, **kwargs):  # DLA-34
    model_kwargs = dict(
        levels=[1, 1, 1, 2, 2, 1], channels=[16, 32, 64, 128, 256, 512],
        block=DlaBasic, **kwargs)
    return _create_dla('dla34', pretrained, **model_kwargs)

网络的前向结构如下

def forward_features(self, x):  # (1,3,224,224)
    x = self.base_layer(x)  # (1,16,224,224)
    x = self.level0(x)  # (1,16,224,224)
    x = self.level1(x)  # (1,32,112,112)
    x = self.level2(x)  # (1,64,56,56)
    x = self.level3(x)  # (1,128,28,28)
    x = self.level4(x)  # (1,256,14,14)
    x = self.level5(x)  # (1,512,7,7)
    return x

其中self.base_layer，self.level0，self.level1的结构如下

Sequential(
  (0): Conv2d(3, 16, kernel_size=(7, 7), stride=(1, 1), padding=(3, 3), bias=False)
  (1): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (2): ReLU(inplace=True)
)
Sequential(
  (0): Conv2d(16, 16, kernel_size=(3, 3), stride=(1, 1), padding=(1, 1), bias=False)
  (1): BatchNorm2d(16, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (2): ReLU(inplace=True)
)
Sequential(
  (0): Conv2d(16, 32, kernel_size=(3, 3), stride=(2, 2), padding=(1, 1), bias=False)
  (1): BatchNorm2d(32, eps=1e-05, momentum=0.1, affine=True, track_running_stats=True)
  (2): ReLU(inplace=True)
)

self.level2 - self.level5都是DLA结构

self.level2 = DlaTree(levels[2], block, channels[1], channels[2], 2, level_root=False, **cargs)
self.level3 = DlaTree(levels[3], block, channels[2], channels[3], 2, level_root=True, **cargs)
self.level4 = DlaTree(levels[4], block, channels[3], channels[4], 2, level_root=True, **cargs)
self.level5 = DlaTree(levels[5], block, channels[4], channels[5], 2, level_root=True, **cargs)

DLATree的实现如下

class DlaTree(nn.Module):
    def __init__(
            self, levels, block, in_channels, out_channels, stride=1, dilation=1, cardinality=1,
            base_width=64, level_root=False, root_dim=0, root_kernel_size=1, root_shortcut=False):
        super(DlaTree, self).__init__()
        if root_dim == 0:
            root_dim = 2 * out_channels
        if level_root:  # level_root表示需要加上上一个stage的绿框
            root_dim += in_channels
        self.downsample = nn.MaxPool2d(stride, stride=stride) if stride > 1 else nn.Identity()
        self.project = nn.Identity()
        cargs = dict(dilation=dilation, cardinality=cardinality, base_width=base_width)
        if levels == 1:
            self.tree1 = block(in_channels, out_channels, stride, **cargs)
            self.tree2 = block(out_channels, out_channels, 1, **cargs)
            if in_channels != out_channels:
                # NOTE the official impl/weights have  project layers in levels > 1 case that are never
                # used, I've moved the project layer here to avoid wasted params but old checkpoints will
                # need strict=False while loading.
                self.project = nn.Sequential(
                    nn.Conv2d(in_channels, out_channels, kernel_size=1, stride=1, bias=False),
                    nn.BatchNorm2d(out_channels))
            self.root = DlaRoot(root_dim, out_channels, root_kernel_size, root_shortcut)
        else:
            cargs.update(dict(root_kernel_size=root_kernel_size, root_shortcut=root_shortcut))
            self.tree1 = DlaTree(
                levels - 1, block, in_channels, out_channels, stride, root_dim=0, **cargs)
            self.tree2 = DlaTree(
                levels - 1, block, out_channels, out_channels, root_dim=root_dim + out_channels, **cargs)
            self.root = None
        self.level_root = level_root
        self.root_dim = root_dim
        self.levels = levels

    def forward(self, x, shortcut: Optional[torch.Tensor] = None, children: Optional[List[torch.Tensor]] = None):
        if children is None:
            children = []
        bottom = self.downsample(x)
        shortcut = self.project(bottom)
        if self.level_root:
            children.append(bottom)  # 上一个stage的绿框
        x1 = self.tree1(x, shortcut)
        if self.root is not None:  # levels == 1
            x2 = self.tree2(x1)
            x = self.root([x2, x1] + children)  # x2是绿框正下面的黑框，x1是绿框左下角的黑框，children是所有输入绿框（包括同一和上一阶段）
        else:
            children.append(x1)  # 同一个stage前面的绿框
            x = self.tree2(x1, None, children)
        return x

这里可以对照图3看，首先self.level2中的level=1，对应图3中第一个红框，这里tree1和tree2都是basic block，树的高度为1没有子树。forward中最后的x1和x2分别对应图3中绿框左下的黑框和正下方的黑框。self.level2的入参level_root=False，在初始化时只有当level_root=True时，root_dim才加上in_channels，这里的in_channles表示这一阶段的输入通道数如图3所示即上一阶段最后一个绿框的通道数。

再看self.level3，levels=2了，左子树self.tree1和右子树self.tree2分别递归调用DlaTree，forward函数中，self.tree1得到的x1是左下的第一个绿框，列表children里存的是上一个stage最后的绿框以及当前stage中除最后输出绿框外所有前面的绿框。self.tree2的输入包括第一个绿框x1和children，对x1处理后得到右下的两个黑框[x1, x2]并与children拼接起来得到四个输入经过self.root的处理得到最终输出。