文章来源于我的个人公众号:KAU的云实验台,主要更新智能优化算法的原理、应用、改进
CEC2005中的测试
本文KAU将介绍一个由Abualigah等人于2021年发表在Comput. Methods Appl. Mech. Eng.上的元启发式算法——算术优化算法(Arithmetic Optimization Algorithm,AOA)[1]

AOA算法的设计很有意思,其巧妙的利用了数学中的加减乘除,乘除运算具有分散度高的性质,用于全局搜索,加减则具有分散度较低的性质,应用于局部搜索。AOA具有无需调整参数、可移植性强、收敛速度快等优点,其性能较之蚁狮、樽海鞘、灰狼等同样具有很强的竞争力,目前已应用于模式识别、神经网络、任务调度等实际问题中。
图源文献[1]
本文将介绍AOA原理、改进及其利用,并在给出算法的MATLAB和Python实现。
00 目录
1 算术优化算法 (AOA)原理
2 代码目录
3 算法性能
4 源码获取
01 算术优化算法 (AOA)原理
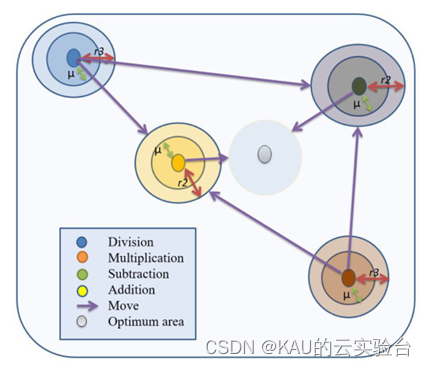
图源文献[1]
AOA是基于种群的元启发式算法,由算术中的四则运算法则来实现全局寻优,通过数学优化器加速函数选择优化策略,其由勘探(乘除)和开发(加减)两个阶段进行参数的优化,具有结构简单,收敛快的特点。下面讲解AOA原理:
1.1 初始化
首先,个体的位置可视为搜索代理,其遵循随机初始化的方法:
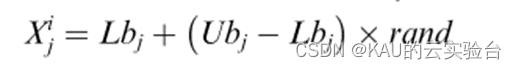
其次,AOA开始迭代寻优前需要根据数学优化器加速函数(Math Optimizer Accelerated,MOA)选择搜索阶段(勘探或开发),MOA的计算如下:
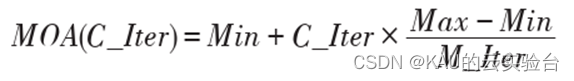
定义一个随机数r1,当r1<MOA时,进入勘探阶段,否则进入开发阶段。C_Iter为当前迭代次数,M_Iter为最大迭代次数,Min和Max为加速函数的最小/大值。
另外,为探索解空间的不同区域,保证解的多样化,AOA更新公式中考虑了一个随机参数,即数学优化概率(Math Optimizer Probability,MOP),MOP的计算如下:
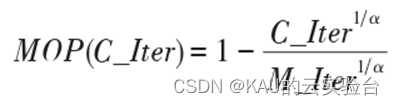
其中,α是敏感参数,定义了迭代过程中的开发精度,取5。
1.2 勘探阶段
乘法和除法运算符分散性高,因此AOA基于除法运算符和乘法运算符进行全局搜索,可以表示为:
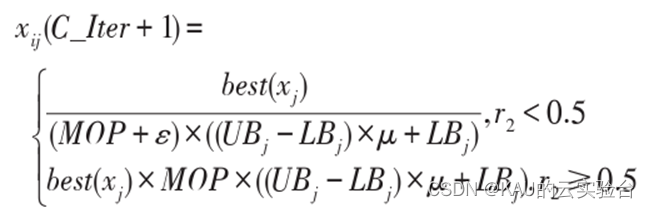
其中,r2∈[0,1],μ=0.499,为搜索过程控制参数。
1.3 开发阶段
加法和减法运算符分散性低,因此AOA基于加法运算符和减法运算符进行局部开发,可以表示为:
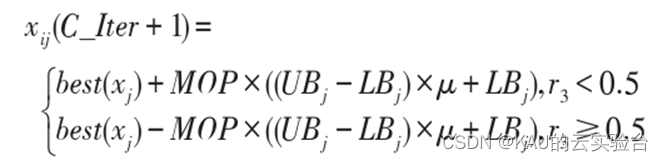
其中,r3∈[0,1]。
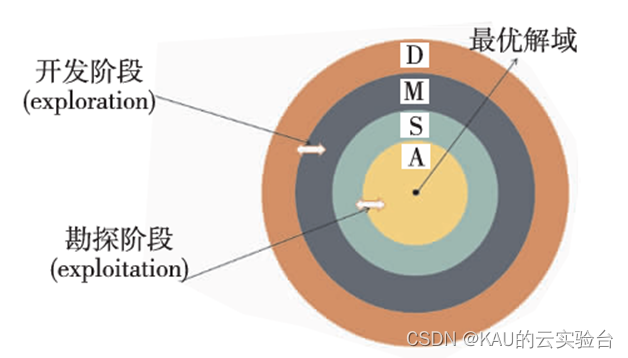
图源文献[2]
1.4 算法流程
AOA的整个算法已介绍完毕,特点就是非常简单明了,易于移植与嵌入。
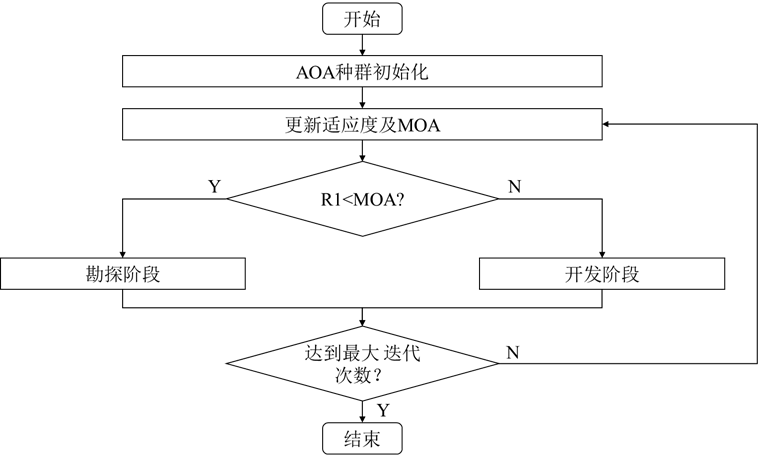
1.5 算法利用&改进
首先,AOA的算法框架简单明了,勘探与开发阶段清晰,非常便于嵌入修改或利用,其勘探阶段中的乘除算子以及开发阶段中的加减算子都可引入其他算法中。同时,其MOP也是个有趣的概念,其在AOA的勘探和开发阶段都使用到了,控制了算法开发精度,也可以加以利用。
其次,AOA的MOA呈现线性递增的趋势,由于其决定了勘探与开发阶段的选择,因此针对不同复杂度的问题,其形式可以进行改变;同样,其开发与勘探阶段的公式同样可以融入其他具有更强搜索能力的策略,比如融入具有强全局搜索能力的黄金正弦方法。最后,可以引入一些“变异”策略,以提高算法跳出局部最远的能力。
02 代码目录
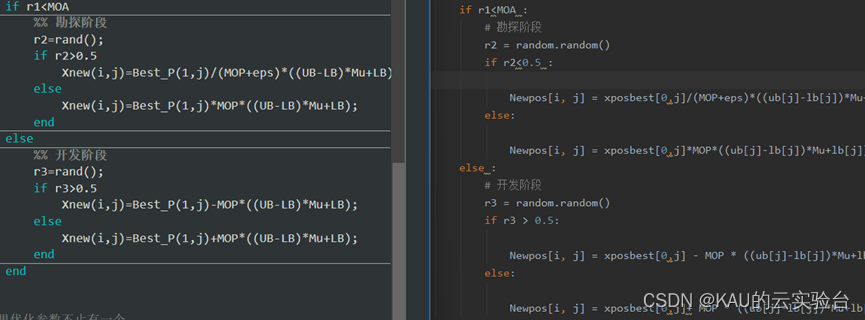
(左Matlab,右Python)
代码包含MATLAB和Python,Python代码为KAU按照Matlab代码手搓而成。考虑到很多同学获取代码后,MATLAB代码部分有乱码(MATLAB版本问题),有几个方法:
①可以将MATLAB版本改为2020及以上;
②将m文件用记事本打开,再将记事本中的代码复制到Matlab;
代码都经过KAU重新注释,代码更清爽,可读性强。
03 算法性能
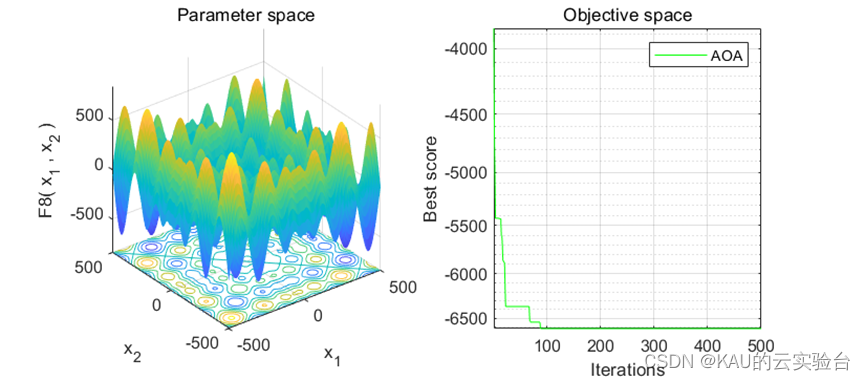
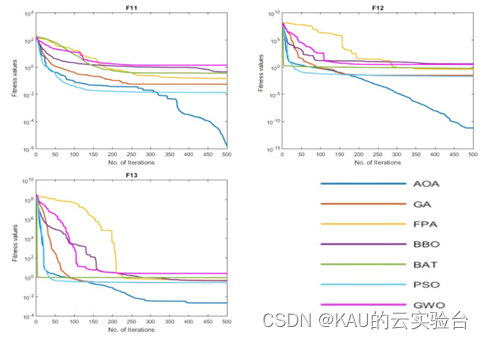
采用标准测试函数初步检验其寻优性能
在MATLAB中,进行标准函数的测试,执行程序结果如下:
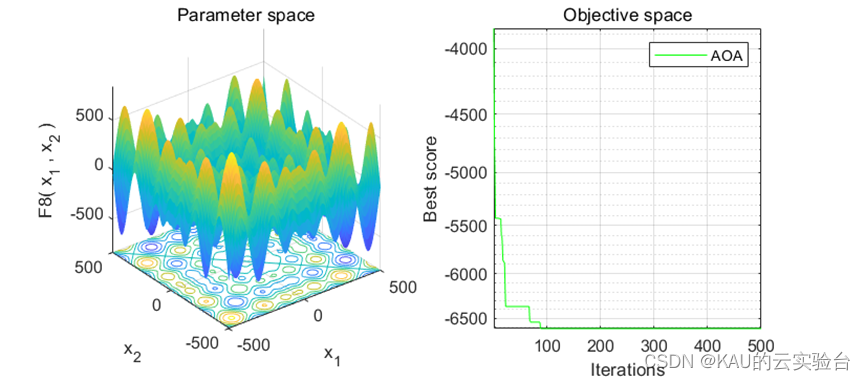
在Python中,进行标准函数的测试,执行程序结果如下:
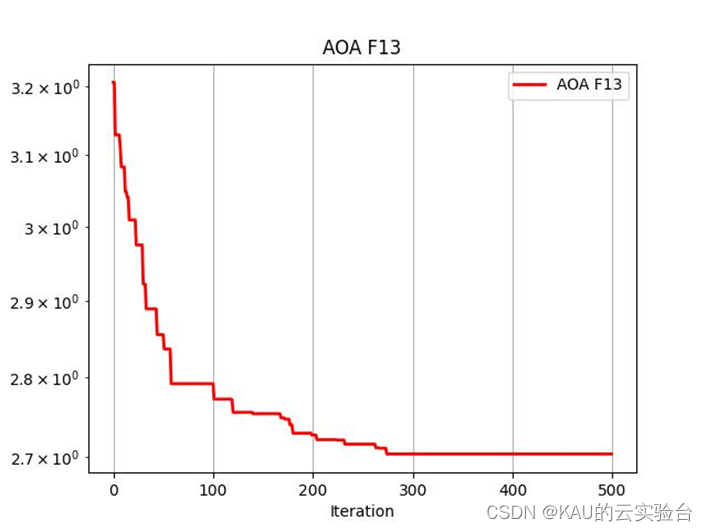
MATLAB和Python都进行了F13函数的测试,测试效果都不错,其收敛速度和精度很好。
04 源码获取
在公众号后台回复 AOA 即可
后续KAU将更新关于AOA的原创改进算法,感兴趣的话可以关注一波~ 新的文章将第一时间推送~
参考文献
[1] ABUALIGAH L, DIANAT A, MIRJALILI S, et al. The arithmetic optimization algorithm[J]. Computer Methods in Applied Mechanics and Engineering, 2021, 376: 113609.
[2]郑婷婷,刘升,叶旭.自适应t分布与动态边界策略改进的算术优化算法[J].计算机应用研究,2022,39(5):1410-1414.
另:如果有伙伴有待解决的优化问题(各种领域都可),可以发我,我会选择性的更新利用优化算法解决这些问题的文章。
如果这篇文章对你有帮助或启发,可以点击右下角的赞/在看(ง •̀_•́)ง(不点也行),你们的鼓励就是我坚持的动力!若有定制需求,可私信作者。