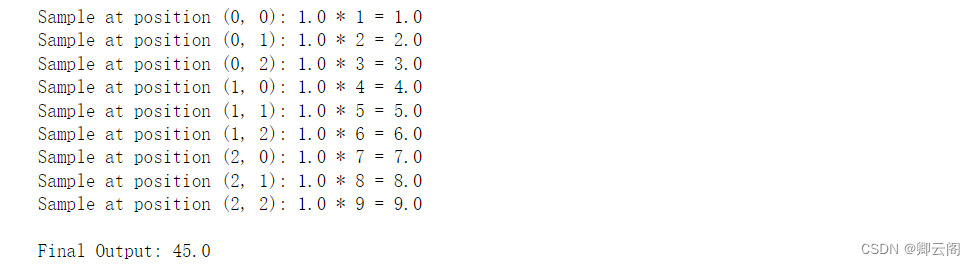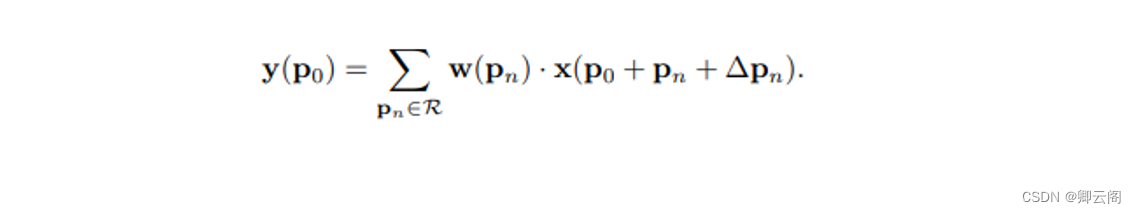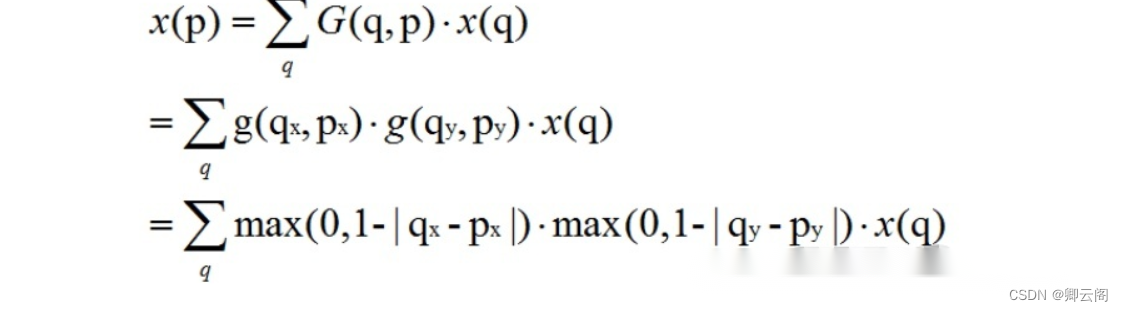🌞欢迎来到Pytorch的世界
🌈博客主页:卿云阁💌欢迎关注🎉点赞👍收藏⭐️留言📝
🌟本文由卿云阁原创!
📆首发时间:🌹2024年2月20日🌹
✉️希望可以和大家一起完成进阶之路!
🙏作者水平很有限,如果发现错误,请留言轰炸哦!万分感谢!
论文地址:
1703.06211.pdf (arxiv.org)
引入
传统卷积的感受野是固定的,无法灵活适应目标的不规则形状。Deformable Convolutional Networks(DCN)旨在通过引入可变形卷积(Deformable Convolution)来解决这一问题。
核心思想
可变形卷积的核心思想是在卷积操作中引入可学习的偏移量,使得网络能够动态地调整卷积核在输入上的采样位置。这种方式可以使网络更好地适应目标的形变,从而提高对不规则目标的识别能力。
主要贡献:
- 可变形卷积: 提出了一种新的可变形卷积操作,可以自适应地调整卷积核的采样位置。
- 可变形ROIPooling: 在目标检测任务中引入了可变形的ROIPooling操作,提高了网络对目标不规则形状的适应性。
- 实验证明: 在多个数据集和任务上进行了实验证明,证明了DCN在目标检测等任务上的优越性。
可变形卷积
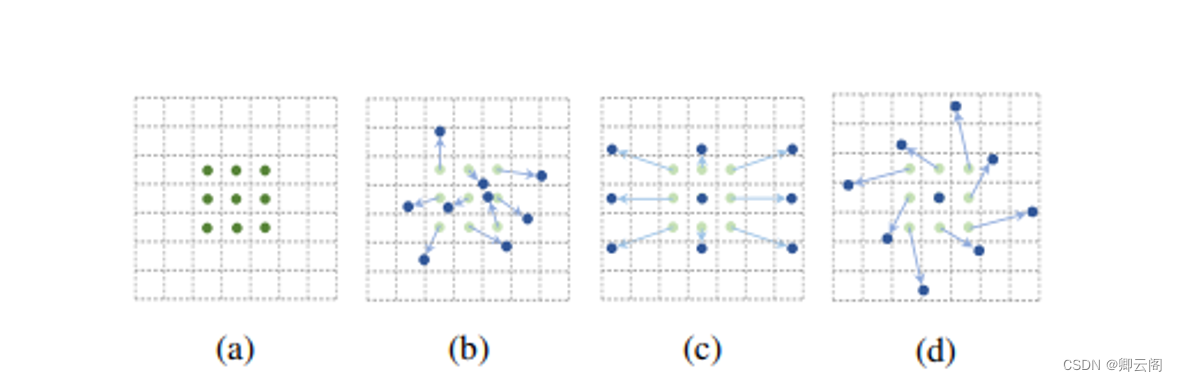
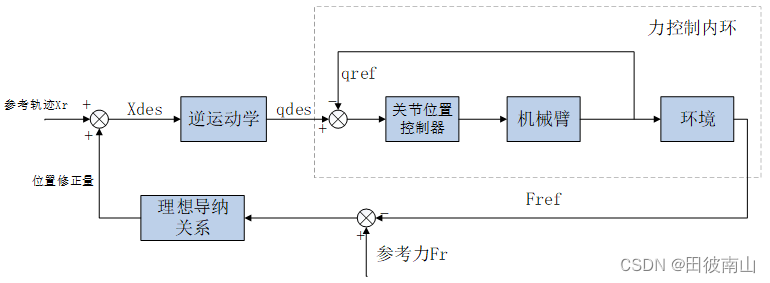
文章提出了可变卷积,添加了位移变量,这个变量根据数据的情况学习,偏移后,相当于卷积核每个方块可伸缩的变化,从而改变了感受野的范围,感受野成了一个多边形。
(a)是普通的卷积,卷积核大小为3*3,采样点排列非常规则,是一个正方形。
(b)是可变形的卷积,给每个采样点加一个offset(这个offset通过额外的卷积层学习得到),排列变得不规则。
(c)和(d)是可变形卷积的两种特例。
(c)加上offset,达到尺度变换的效果
(d)加上offset,达到旋转变换的效果。
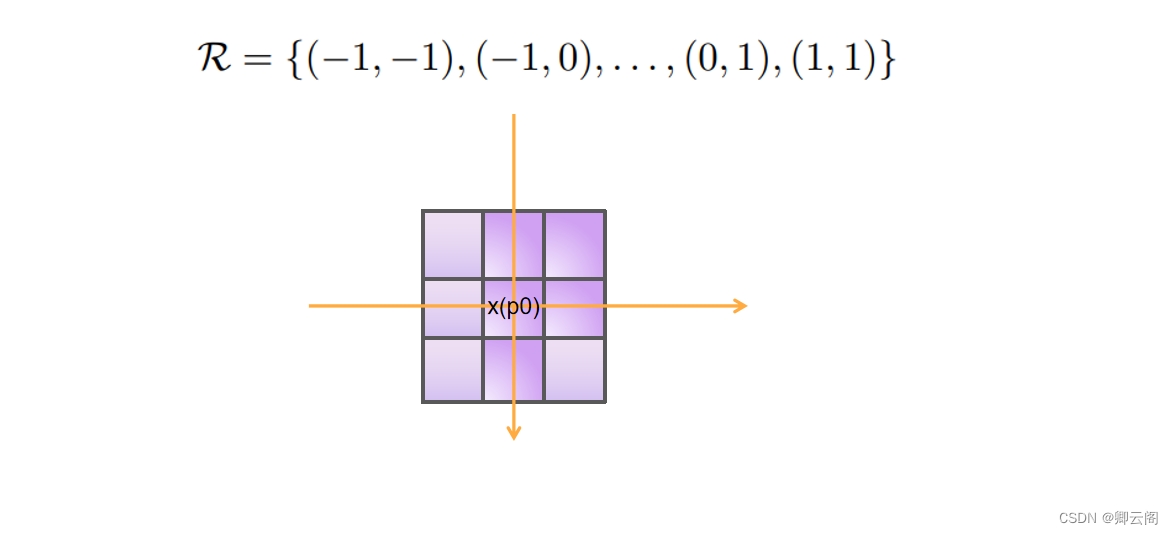
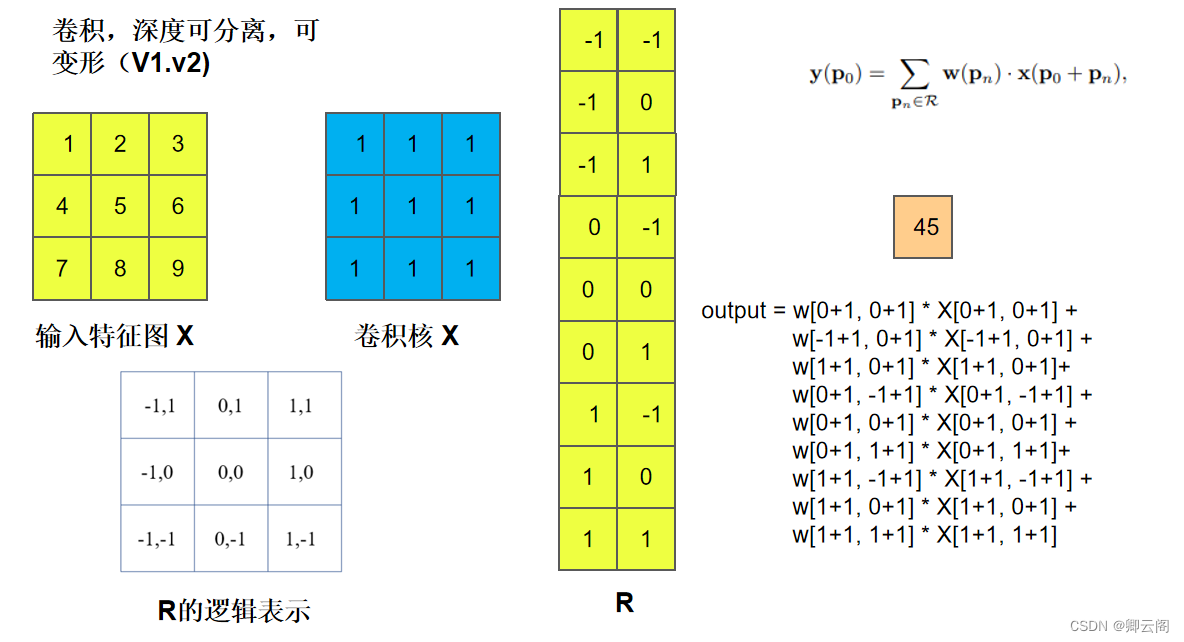
我们先看普通的卷积,以3x3卷积为例对于每个输出y(p0),都要从x上采样9个位置,这9个位置都在中心位置x(p0)向四周扩散,(-1,-1)代表x(p0)的左上角,(1,1)代表x(p0)的右下角。
(R 中的(−1, −1) 表示卷积核(或感受野)相对于中心位置的一个位置偏移。每个元素 (i, j) 表示相对于中心位置的水平偏移 i 和垂直偏移 j。
对于 (−1, −1),水平偏移为 -1,垂直偏移也为 -1。这表示卷积核在水平和垂直方向上都相对于中心位置向左上方移动一个位置。在卷积操作中,这个偏移会影响卷积核在输入特征图上的采样位置,进而影响卷积操作的结果。
这个网格 R 中的元素定义了卷积核的形状和采样策略,影响了卷积操作在输入上的感受野。在给定的例子中,R = {(−1, −1),(−1, 0), . . . ,(0, 1),(1, 1)} 表示卷积核的形状是 3 × 3,它在水平和垂直方向上相对于中心位置有一个单位的偏移。)
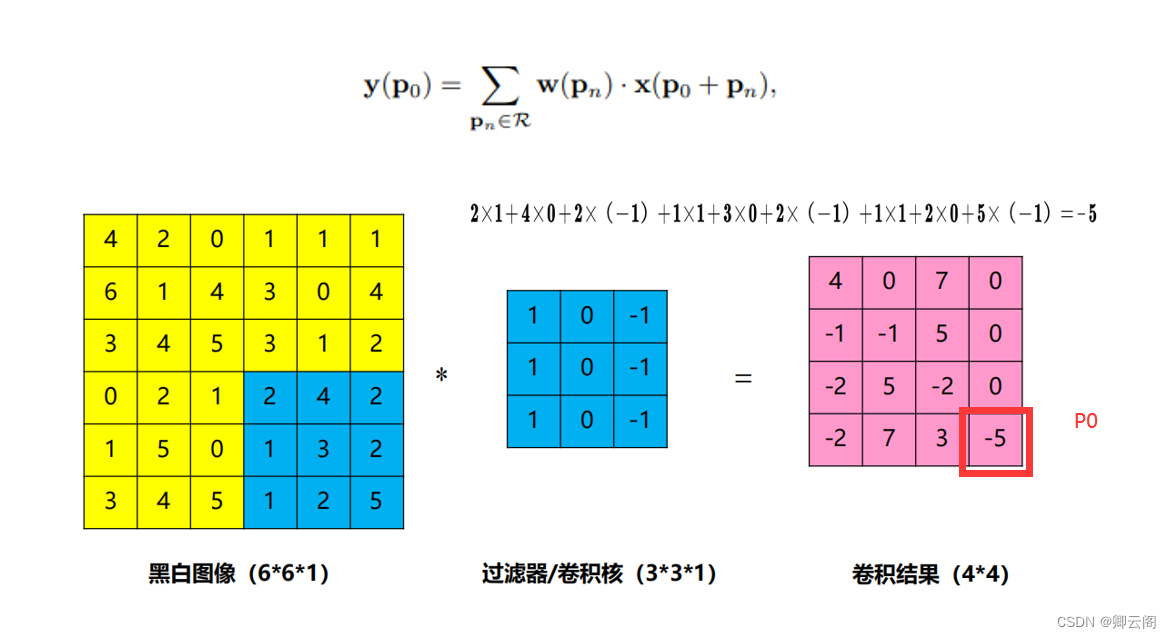
所以传统的卷积输出就是(其中Pn就是网格中的n个点):
举个栗子:
import numpy as np # 定义输入特征图 X X = np.array([[1, 2, 3], [4, 5, 6], [7, 8, 9]]) # 定义卷积核 w 和采样位置 R w = np.ones((3, 3)) # 使用全1权重 R = [(-1, -1), (-1, 0), (-1, 1), (0, -1), (0, 0), (0, 1), (1, -1), (1, 0), (1, 1)] # 初始化输出 output = 0 # 执行卷积操作 for p_n in R: # 输出位置 p_0 = (1 + p_n[0], 1 + p_n[1]) # 计算权重采样 weighted_sample = w[p_0[0], p_0[1]] * X[p_0[0], p_0[1]] # 打印每一步的计算过程 print(f"Sample at position {p_0}: {w[p_0[0], p_0[1]]} * {X[p_0[0], p_0[1]]} = {weighted_sample}") # 更新输出 output += weighted_sample # 输出最终结果 print("\nFinal Output:", output)
可变形卷积则在公式1的基础上为每个点引入了一个偏移量,偏移量是由输入特征图与另一个卷积生成的,通常是小数。
由于加入偏移量后的位置一般为小数,并不对应输入特征图上实际的像素点,因此需要使用插值来得到偏移后的像素值,通常可采用双线性插值,用公式表示如下:
其中,公式中最后一行的max(0, 1-...)限制了插值点与邻域点不超过1个像素的距离。
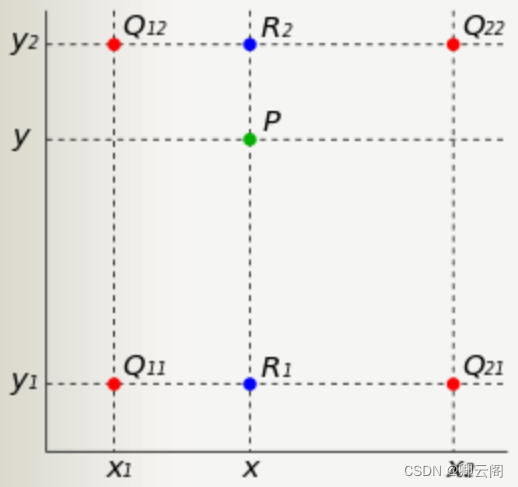
双线性插值是指将插值点位置的像素值设为其4邻域像素点的加权和,邻域4个点是离其最近的在特征图上实际存在的像素点,每个点的加权权重则根据它与插值点横、纵坐标的距离来设置,最终得到插值点的像素值。
各点权重由各点距离P点的距离确定。
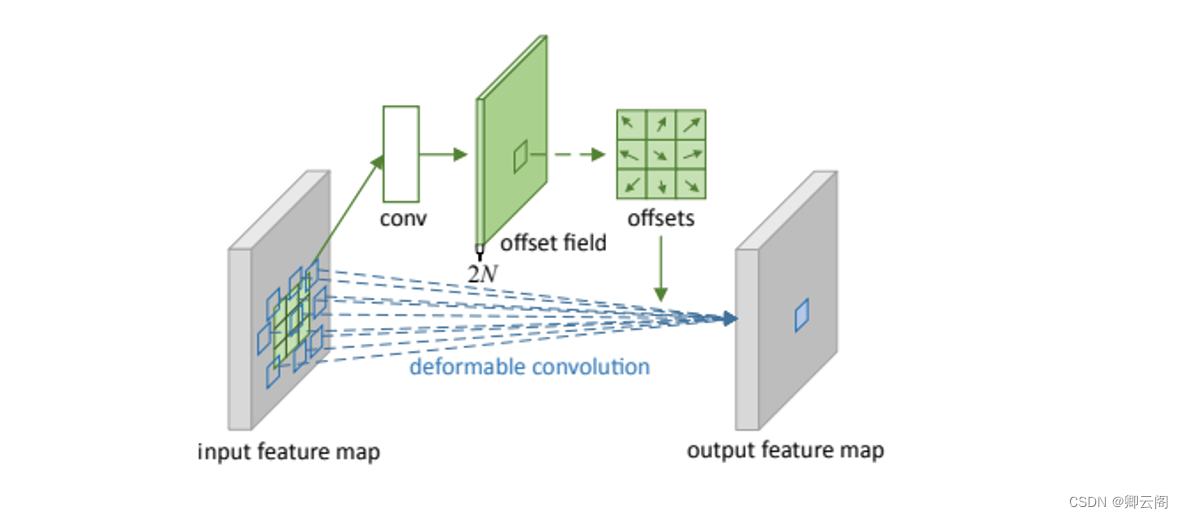
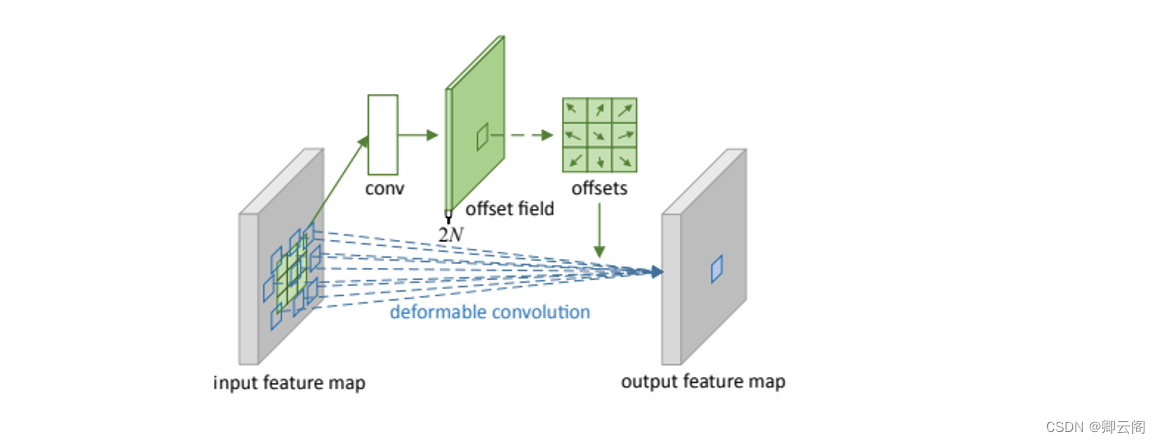
下图为可变形卷积示意图。可以看到offsets(偏移)是额外使用一个卷积来生成的,与最终要做卷积操作那个卷积不是同一个 。图示N为卷积核区域大小,例如3*3大小的卷积核,N=9,图中绿色过程为卷积学习偏移的过程,其中offset field的通道大小为2N,表示卷积核分别学习x方向与y方向的偏移量。下图所示,在input feature map上普通卷积操作对应卷积采样区域是一个卷积核大小的正方形(绿框),而可变形卷积对应的卷积采样区域为一些蓝框表示的点,这就是可变形卷积与普通卷积的区别。
可变形卷积的具体细节:
- 一个output feature map上的点对应到input feature map上的卷积采样区域大小为K*K,按照可变形卷积的操作,这K*K区域的每一个卷积采样点都要学习一个偏离量offset,而offset是用坐标表示的,所以一个output要学习2*K*K个参数。假设一个output大小为H*W,所以一共要学习2*K*K*H*W个参数。即上图的offset field(N=K*K),其维度为B*2*K*K*H*W,其中B代表batch_size;
- 假设input feature map的维度为B*C*H*W,一个batch内的特征图(一共C个)共用一个offset field,即一个batch内的每张特征图用到的偏移量是一样的;
- 可变形卷积不改变input feature map的尺寸,所以output feature map也为H x W;
【Deep Learning 6】可变形卷积
news2026/2/15 10:56:18
本文来自互联网用户投稿,该文观点仅代表作者本人,不代表本站立场。本站仅提供信息存储空间服务,不拥有所有权,不承担相关法律责任。如若转载,请注明出处:http://www.coloradmin.cn/o/1460866.html
如若内容造成侵权/违法违规/事实不符,请联系多彩编程网进行投诉反馈,一经查实,立即删除!相关文章
想了解黄金代理的资质应该看什么?
投资者要选择黄金代理为自己开户和服务,自然关于代理的资质是很重要的,那怎么判断黄金代理的资质是好是坏呢?下面我们就来讨论一下。我们主要可以从以下这几个方面来讨论黄金代理的资质。 首先就是黄金代理背后的黄金交易平台的牌照是什么&am…
java 使用documents4j将XML转为pdf文件的方式
1.背景:
通过spire.doc.free将word转换成PDF时存在缺陷:只能获取前3页。获取全文另外需支付费用。 2.解决办法
使用documents4j,documents4j会保留原word文件中更多的样式,如修订模式下的差异化字体颜色、文档右侧修订记录等。 …
PHP实践:Laravel中事件使用讲解
🏆作者简介,黑夜开发者,CSDN领军人物,全栈领域优质创作者✌,CSDN博客专家,阿里云社区专家博主,2023年6月CSDN上海赛道top4。 🏆数年电商行业从业经验,历任核心研发工程师…
js设计模式:适配器模式
作用:
可以将某种不同格式的数据转化为自己所期待的数据格式
或者对于一些存在兼容或者特殊处理的业务逻辑,可以进行一个适配
示例: //原始数据let oldData1 [{name: 王惊涛,age: 29},{name: 孙悟空,age: 800},{name: 嘉文四世,age: 27},{name: 关羽,age: 40},{name: 伊利丹…
【Oracle】玩转Oracle数据库(三):数据库的创建和管理
前言 嘿,各位数据库小能手们!今天我们要进入数据库的创世纪,探索Oracle数据库的创建和管理!🔧💻 在这篇博文【Oracle】玩转Oracle数据库(三):数据库的创建和管理中&#…
判断一个dll/exe是32位还是64位
通过记事本判断(可判断C或者C#)
64位、将dll用记事本打开,可以看到一堆乱码,但是找到乱码行的第一个PE,如果后面是d?则为64位
32位、将dll用记事本打开,可以看到一堆乱码,但是找到乱码行的第…
第二证券:可转债怎么套利?可转债常见的六种套利方法
可转债是上市公司为了融资向社会公众所发行的一种债券,其间投资者可以在二级市场上进行套利操作,存在以下六种套利办法:
1、折价转股套利
只有在溢价率为负时,可转债才有套利空间,转股溢价率为正,则不存在…
SmartBi--配置BI启动为后台服务
目录
1. 在service.bat目录下打开cmd
2. 运行 service.bat install 服务名 命令
3.在服务中找到设置的服务名,设置成自启,启动服务即可
4.在tomcat logs目录下查看日志
5. 移除服务 1. 在service.bat目录下打开cmd
2. 运行 service.bat install …
短视频内容如何吸引用户?媒介盒子揭秘
不管是什么行业,在宣传中都会用到短视频这种类型,然而有许多品牌方在宣传时总会面临找不着发力点,宣传内容同质化等问题,今天媒介盒子就来和大家聊聊:什么样的短视频内容能够吸引用户。 一、 制造强烈对比,…
python 批量创建的目录和文件、同时写入文件内容、为短视频做基础模板准备
图: 代码:
import os
def create_directory(path):if not os.path.exists(path):os.makedirs(path)print("已创建目录:", path)else:print("该路径下已存在相同名称的目录")def create_file(filename):with open(filena…
【快速搞定Webpack5】处理字体图标资源(六)
介绍
在实际开发中,几乎每个项目都需要用户icon图标以及部分项目会用到有特色的字体需求。 今天我们学习的内容就是如何在webpack中处理字体及icon图标的使用。
一、下载字体图标文件
1、打开 阿里巴巴矢量图库 2、登录或注册账号 3、选择想要的图标添加到购物车…
04 动力云客之登录后获取用户信息+JWT存进Redis+Filter验证Token + token续期
1. 登录后获取用户信息
非常好实现. 只要新建一个controller, 并调用SS提供的Authentication对象即可
package com.sunsplanter.controller;RestController
public class UserController {GetMapping(value "api/login/info")public R loginInfo(Authentication a…
ipad作为扩展屏的最简单方式(无需数据线)
ipad和win都下载安装toDesk,并且都处于同一局域网下
连接ipad,在ipad中输入win设备的设备密码和临时密码,连接上后可以看到ipad会是win屏幕的镜像,此时退出连接,准备以扩展模式再次连接。
注意,如果直接从…
FPGA高端项目:FPGA实现SDI视频编解码工程解决方案,提供3套工程源码和技术支持
目录 1、前言免责声明 2、相关方案推荐本博已有的 SDI 编解码方案本方案的SDI图像缩放应用本方案的SDI图像缩放视频拼接应用本方案的SDI图像缩放UDP网络视频发送应用本方案的SDI视频编码输出应用本方案的SDI视频编码图像缩放视频拼接输出应用本方案的SDI视频编码SFP光口收发应用…
如何在Ubuntu部署Emlog,并将本地博客发布至公网可远程访问
文章目录 前言1. 网站搭建1.1 Emolog网页下载和安装1.2 网页测试1.3 cpolar的安装和注册 2. 本地网页发布2.1 Cpolar临时数据隧道2.2.Cpolar稳定隧道(云端设置)2.3.Cpolar稳定隧道(本地设置) 3. 公网访问测试总结 前言
博客作为使…
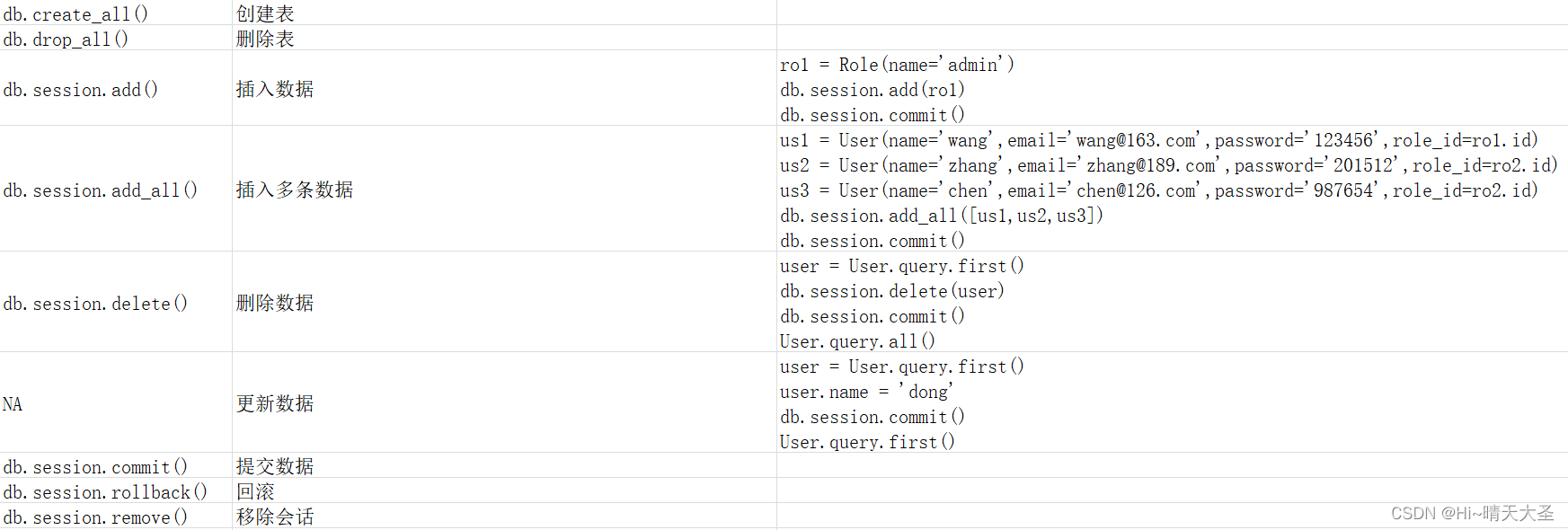
Flask数据库操作-Flask-SQLAlchemy
Flask中一般使用flask-sqlalchemy来操作数据库。flask-sqlalchemy的使用介绍如下:
一、SQLAlchemy
SQLALchemy 实际上是对数据库的抽象,让开发者不用直接和 SQL 语句打交道,而是通过 Python 对象来操作数据库,在舍弃一些性能开销…